人教版数学九年级上册 23.1 图形的旋转 上课同步课件(共14张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.1 图形的旋转 上课同步课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 20:19:38 | ||
图片预览



文档简介
B
O
A
45
0
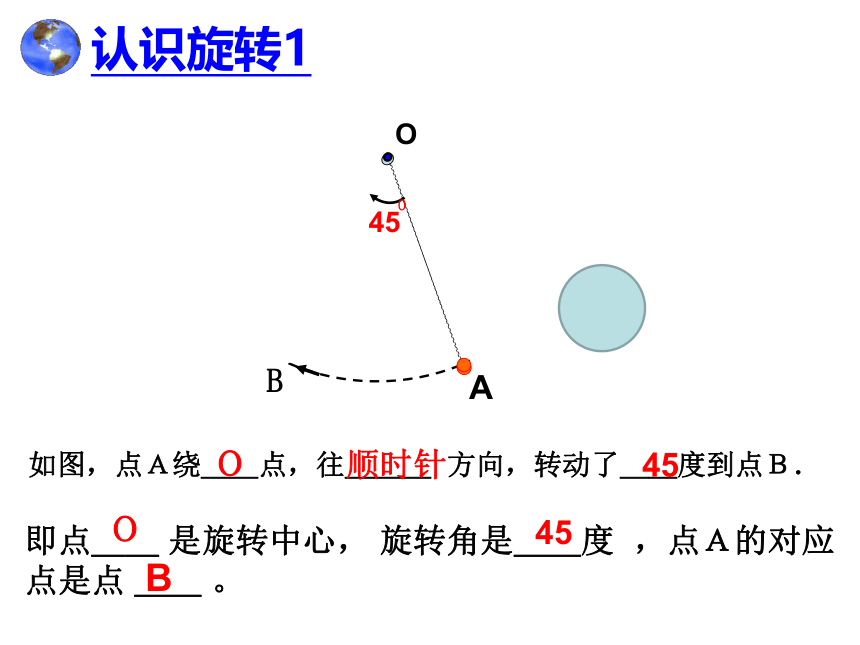
如图,点A绕__点,往___ 方向,转动了__度到点B.
O
顺时针
45
认识旋转1
即点__ 是旋转中心, 旋转角是__度 ,点A的对应点是点 __ 。
O
45
B
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
练习1:
练习2:
B
A
探究
B?
A?
C
C?
O
100
0
对应点到旋转中心的距离相等.
旋转前、后的图形全等。
对应点与旋转中心所连线段的夹角等于旋转角.
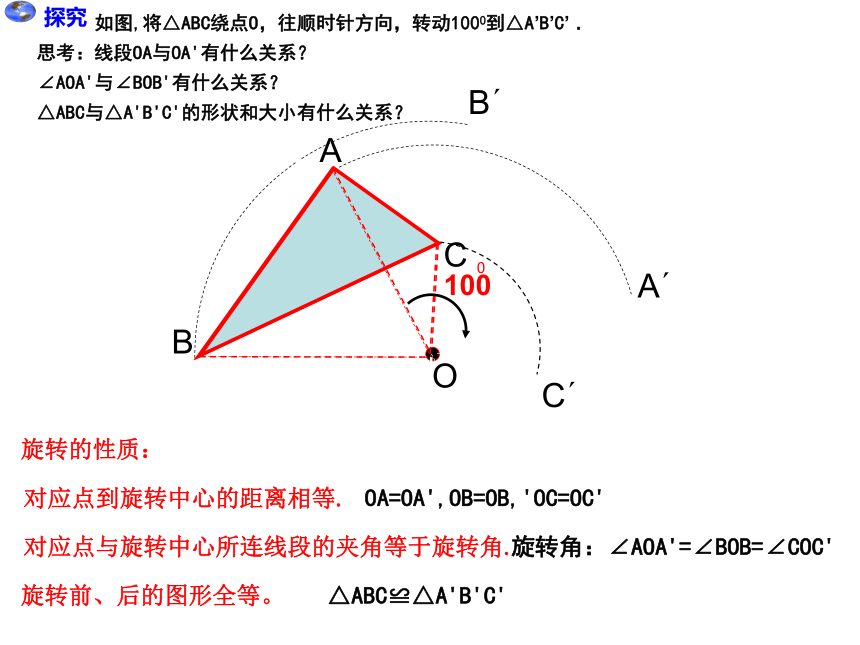
旋转的性质:
如图,将△ABC绕点O,往顺时针方向,转动1000到△A’B’C’ .
思考:线段OA与OA'有什么关系?
∠AOA'与∠BOB'有什么关系?
△ABC与△A'B'C'的形状和大小有什么关系?
OA=OA',OB=OB,'OC=OC'
旋转角:∠AOA'=∠BOB=∠COC'
△ABC≌△A'B'C'
600
3000
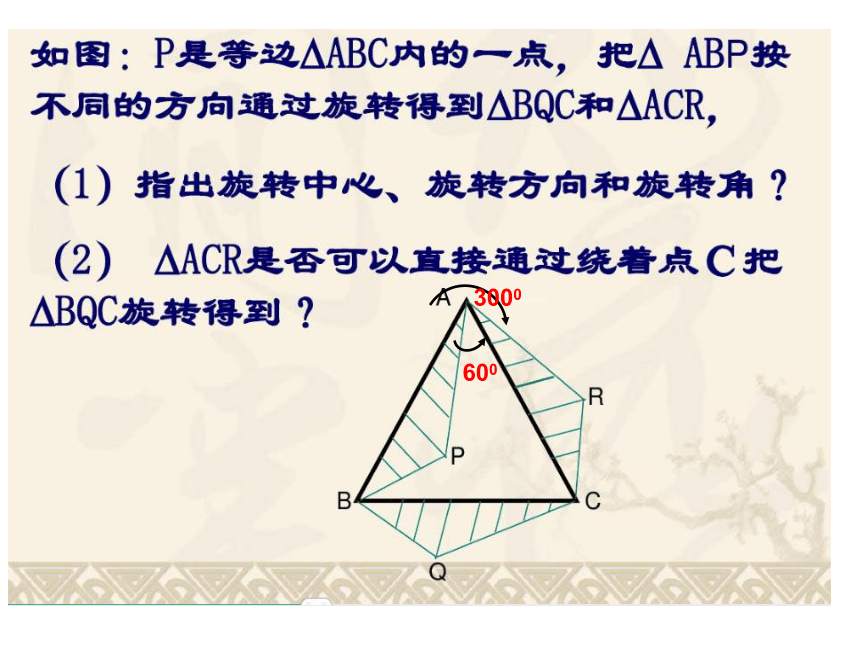
将等边△ABC绕着点o按某个方向旋转900后得到△A1B1C1
A
B
C
.
0
C1
B1
A1
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
旋转前、后的图形全等.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心所连线段的夹角等于旋转角.
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
议一议
练一练
(1)旋转中心是哪一点?
(2)旋转角是多少度?
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G
D
H
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别转到
什么位置?
(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.旋转前、后
的图形全等.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
O
A
45
0
如图,点A绕__点,往___ 方向,转动了__度到点B.
O
顺时针
45
认识旋转1
即点__ 是旋转中心, 旋转角是__度 ,点A的对应点是点 __ 。
O
45
B
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
练习1:
练习2:
B
A
探究
B?
A?
C
C?
O
100
0
对应点到旋转中心的距离相等.
旋转前、后的图形全等。
对应点与旋转中心所连线段的夹角等于旋转角.
旋转的性质:
如图,将△ABC绕点O,往顺时针方向,转动1000到△A’B’C’ .
思考:线段OA与OA'有什么关系?
∠AOA'与∠BOB'有什么关系?
△ABC与△A'B'C'的形状和大小有什么关系?
OA=OA',OB=OB,'OC=OC'
旋转角:∠AOA'=∠BOB=∠COC'
△ABC≌△A'B'C'
600
3000
将等边△ABC绕着点o按某个方向旋转900后得到△A1B1C1
A
B
C
.
0
C1
B1
A1
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
旋转前、后的图形全等.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心所连线段的夹角等于旋转角.
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
议一议
练一练
(1)旋转中心是哪一点?
(2)旋转角是多少度?
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G
D
H
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别转到
什么位置?
(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.旋转前、后
的图形全等.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
同课章节目录
