人教版数学九年级上册 23.1 图形的旋转(第1课时)教学课件(共16张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.1 图形的旋转(第1课时)教学课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 294.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 20:22:04 | ||
图片预览



文档简介
第二十三章 旋转
23.1 图形的旋转
23.1 图形的旋转(第1课时)
情景问题: 这些情景中的转动现象,有什么共同特征?
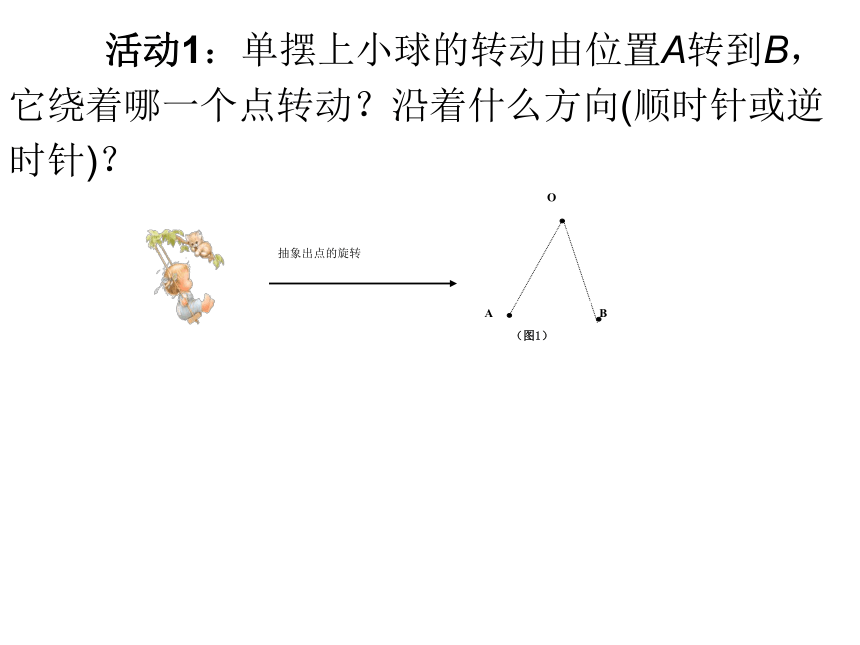
活动1:单摆上小球的转动由位置A转到B,
它绕着哪一个点转动?沿着什么方向(顺时针或逆
时针)?
抽象出点的旋转
A
B
(图1)
O
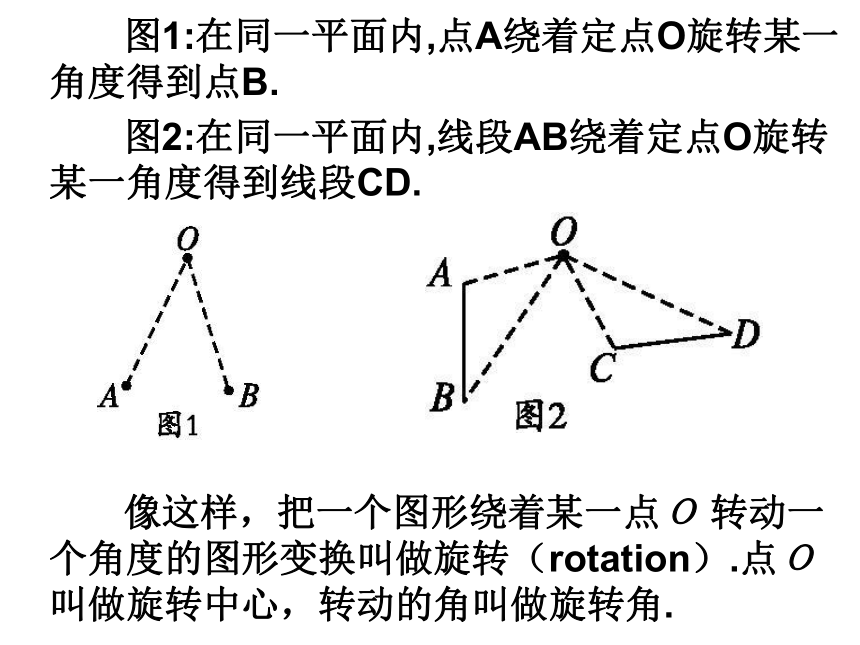
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B.
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD.
像这样,把一个图形绕着某一点O 转动一个角度的图形变换叫做旋转(rotation).点O 叫做旋转中心,转动的角叫做旋转角.
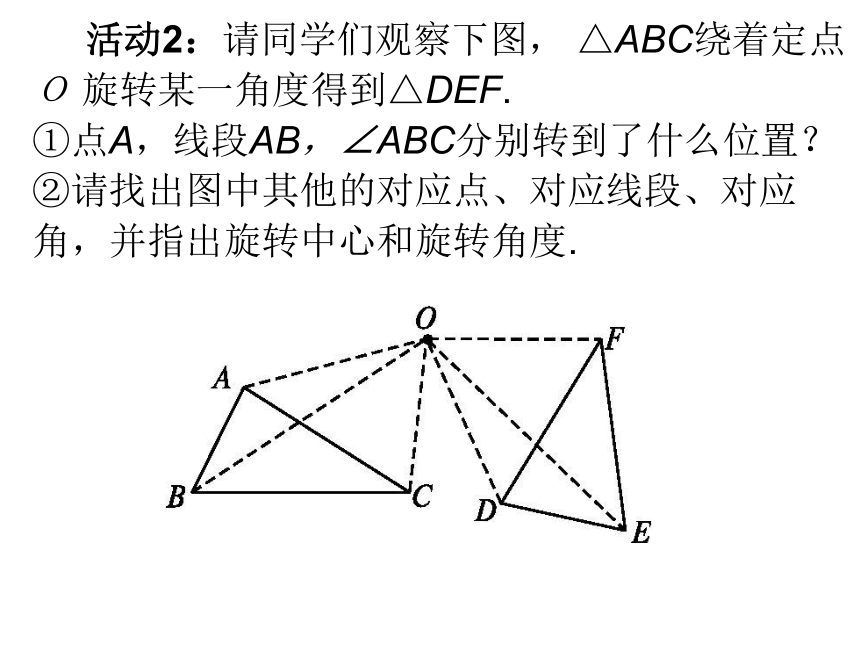
活动2:请同学们观察下图, △ABC绕着定点
O 旋转某一角度得到△DEF.
①点A,线段AB,∠ABC分别转到了什么位置?
②请找出图中其他的对应点、对应线段、对应
角,并指出旋转中心和旋转角度.
活动3:如图,香港特别行政区区旗中央的
紫荆花图案由5个相同的花瓣组成,它是由其中的
一瓣经过几次旋转得到的? 旋转角∠AOB多少度?
你知道∠COD等于多少度吗?
·
·
A
B
O
D
C
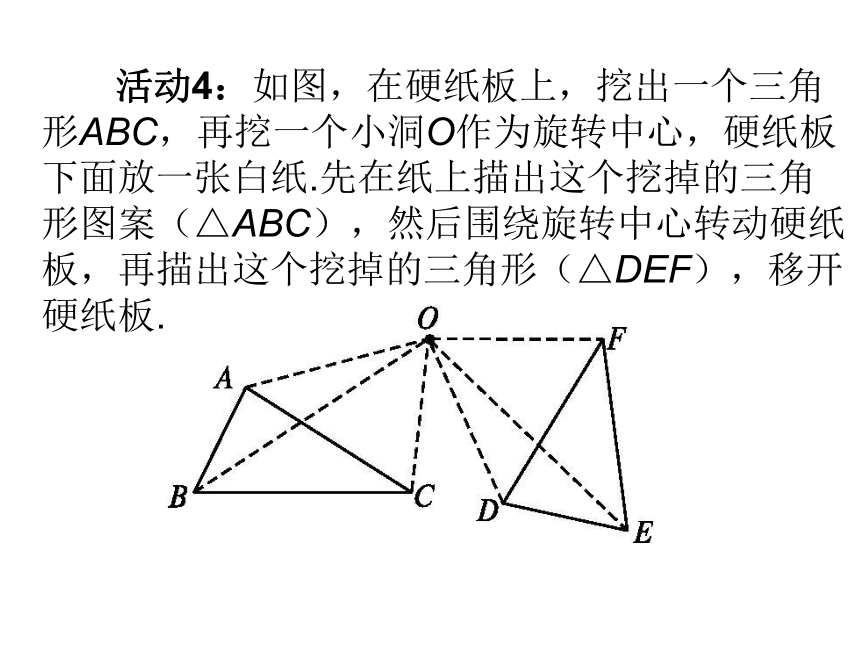
活动4:如图,在硬纸板上,挖出一个三角形ABC,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△DEF),移开硬纸板.
问题1:在图形的旋转过程中,线段OA与线段OD的关系怎样?∠AOD与∠BOE呢?△ABC与△DEF呢?
问题2:旋转前后图形的形状和大小有影响吗?
问题3:你能通过度量角的方法得出旋转角度吗?
你准备度量哪个角?
答案:
问题1:OA=OD,∠AOD=∠BOE,△ABC≌△DEF;
问题2:没有;
问题3:能,∠AOD.
归纳出旋转的特征:
1.旋转前后的图形全等;
2.对应点到旋转中心的距离相等;
3.对应点与旋转中心连线段的夹角等于旋转角.
三、课堂练习
1.平面图形的旋转一般情况下改变图形的( )
A.位置 B.大小 C.形状 D.性质
2.经过旋转,对应点到旋转中心的距离 .
3.等边三角形绕着它的三边中线的交点旋转至少 度,能够与本身重合.
4.钟表的分针匀速旋转一周需要60分钟,那么:
(1)它的旋转中心是什么?
(2)分针旋转一周,时针旋转多少度?
(3)下午3点半时,时针和分针的夹角是多少度?
5.E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
(1)旋转中心是哪一点?
(2)如何确定△ADE三个顶点的对应点,即它们旋转后的位置?
(3)以点A为中心,把△ADE逆时针旋转90°,画出旋转后的图形.
6.同学们玩过万花筒吗?如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )得到的.
A.顺时针旋转60° B.顺时针旋转120°
C.逆时针旋转60° D.逆时针旋转120°
7.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A'B'C'.
四、谈谈收获
通过这节课的学习,你有什么收获?
五、布置作业
课本第62页习题23.1第2,3题.
23.1 图形的旋转
23.1 图形的旋转(第1课时)
情景问题: 这些情景中的转动现象,有什么共同特征?
活动1:单摆上小球的转动由位置A转到B,
它绕着哪一个点转动?沿着什么方向(顺时针或逆
时针)?
抽象出点的旋转
A
B
(图1)
O
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B.
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD.
像这样,把一个图形绕着某一点O 转动一个角度的图形变换叫做旋转(rotation).点O 叫做旋转中心,转动的角叫做旋转角.
活动2:请同学们观察下图, △ABC绕着定点
O 旋转某一角度得到△DEF.
①点A,线段AB,∠ABC分别转到了什么位置?
②请找出图中其他的对应点、对应线段、对应
角,并指出旋转中心和旋转角度.
活动3:如图,香港特别行政区区旗中央的
紫荆花图案由5个相同的花瓣组成,它是由其中的
一瓣经过几次旋转得到的? 旋转角∠AOB多少度?
你知道∠COD等于多少度吗?
·
·
A
B
O
D
C
活动4:如图,在硬纸板上,挖出一个三角形ABC,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△DEF),移开硬纸板.
问题1:在图形的旋转过程中,线段OA与线段OD的关系怎样?∠AOD与∠BOE呢?△ABC与△DEF呢?
问题2:旋转前后图形的形状和大小有影响吗?
问题3:你能通过度量角的方法得出旋转角度吗?
你准备度量哪个角?
答案:
问题1:OA=OD,∠AOD=∠BOE,△ABC≌△DEF;
问题2:没有;
问题3:能,∠AOD.
归纳出旋转的特征:
1.旋转前后的图形全等;
2.对应点到旋转中心的距离相等;
3.对应点与旋转中心连线段的夹角等于旋转角.
三、课堂练习
1.平面图形的旋转一般情况下改变图形的( )
A.位置 B.大小 C.形状 D.性质
2.经过旋转,对应点到旋转中心的距离 .
3.等边三角形绕着它的三边中线的交点旋转至少 度,能够与本身重合.
4.钟表的分针匀速旋转一周需要60分钟,那么:
(1)它的旋转中心是什么?
(2)分针旋转一周,时针旋转多少度?
(3)下午3点半时,时针和分针的夹角是多少度?
5.E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
(1)旋转中心是哪一点?
(2)如何确定△ADE三个顶点的对应点,即它们旋转后的位置?
(3)以点A为中心,把△ADE逆时针旋转90°,画出旋转后的图形.
6.同学们玩过万花筒吗?如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )得到的.
A.顺时针旋转60° B.顺时针旋转120°
C.逆时针旋转60° D.逆时针旋转120°
7.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A'B'C'.
四、谈谈收获
通过这节课的学习,你有什么收获?
五、布置作业
课本第62页习题23.1第2,3题.
同课章节目录
