人教版数学九年级上册 24.1.2 垂直于弦的直径 上课课件(共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1.2 垂直于弦的直径 上课课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 536.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览





文档简介
24.1.2垂直于弦的直径
滑县道口镇第一初中 张海英
义务教育教科书
人教版九年级 上册
帮助老师解决问题:
1.老师有一张圆形纸片,却找不准它的圆心,你们能帮我找到它的圆心吗?
2.老师放在办公桌上的一个圆形小镜子,不小心打破了,你们能用破碎的镜片画出镜子原来的圆形吗?
怎么找圆心?
把圆形纸片对折两次,两次折痕交点即为圆心.
通过折叠,我们发现,圆是_________图形,
_______________________都是圆的对称轴.
轴对称
任何一条直径所在的直线
(如图,AB是⊙0的一条弦, CD是⊙0直径)
我们能不能通过改变AB的位置,
使它成为轴对称图形?
下面这个图形是轴对称图形吗?
在你的圆形纸片上画出改变位置后的图形,并尝试折叠验证.
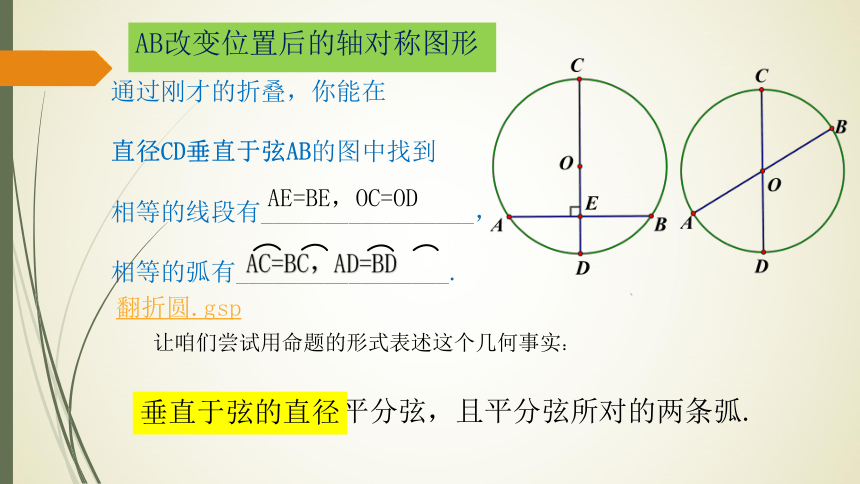
AB改变位置后的轴对称图形
通过刚才的折叠,你能在
直径CD垂直于弦AB的图中找到
相等的线段有_________________,
相等的弧有_________________.
垂直于弦的直径平分弦,且平分弦所对的两条弧.
让咱们尝试用命题的形式表述这个几何事实:
AE=BE,OC=OD
垂直于弦的直径
直径CD垂直于弦AB
翻折圆.gsp
AC=BC,AD=BD
证明:连接OA、OB
∴沿直线CD折叠,则点A、点B能够重合,
在△OAB中,
∵OA=OB,CD⊥AB,
∴AE=BE,即CD垂直平分AB,
也即点A、点B关于直线CD对称,
进而,AC=BC,AD=BD
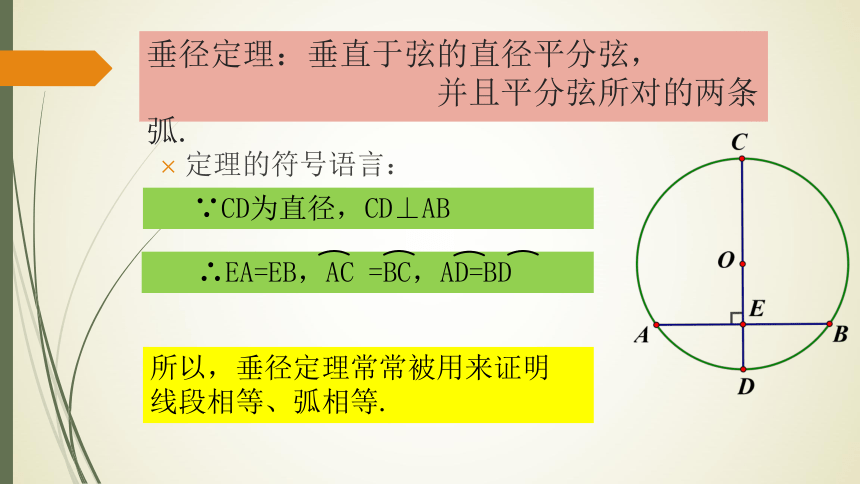
垂径定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
定理的符号语言:
∵CD为直径,CD⊥AB
所以,垂径定理常常被用来证明
线段相等、弧相等.
∴EA=EB,AC =BC,AD=BD
小试牛刀
判断下列图形是否都能使用垂径定理?
归纳:定理中的垂径可以是直径、半径、弦心距等过圆心的直线或线段.
回味定理
条件 结论
垂径定理中涉及的这五个内容分别标号为
①经过圆心, ③平分弦,
④平分弦所对的优弧,
②垂直于理弦, ⑤平分弦所对的劣弧.
CD为直径
CD⊥AB
CD平分弦AB
CD平分弧ADB
CD平分弧ACB
平分弦的直径垂直于弦,并且平分弦所对的两条弧.
(×)
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
回味定理
条件 结论
①经过圆心, ③平分弦,
④平分弦所对的优弧,
②垂直于弦, ⑤平分弦所对的劣弧.
圆对称性分析.gsp
CD为直径
CD⊥AB
CD平分弦AB
CD平分弧ADB
CD平分弧ACB
弦的垂直平分线_____________________________
必过圆心,并且平分弦所对的两条弧.
一显身手
1.如图,AB是⊙0的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BC
2.看图填空:
(1)∵ AB是直径,AB⊥CD
∴ _________________________
(2)∵AB是直径, CE=DE
∴ ___________________________
(3)∵ CE=DE,AB⊥CD
∴ _______________________________
C
CE=DE,AC=AD,BC=BD.
AB⊥CD,AC=AD,BC=BD.
AB经过圆心,AC=AD,BC=BD.
3.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点,求证:AC=BD
添加辅助线,构造垂径定理的基本图形.
证明:作OE⊥AB于E,
则AE=BE,CE=DE
∴ AE-CE=BE-DE
即AC=BD
E
4.如图,在⊙0中,弦AB的长为8cm,圆心O到AB的距离为3cm.求⊙0的半径.
归纳:在圆中,我们常常添加的辅助线是弦心距或半径,构造由半径、半弦、弦心距组成的直角三角形,然后再使用勾股定理解决问题.
解:连接OA,作OE ⊥AB于E,
则AE=12AB=12×8=4.
在Rt △AOE中,
OA=????????2+????????2=32+42=5
答:⊙0的半径为5cm.
?
5.自学课本第82页 例2 赵州桥问题
OD=OC-CD=R-7.23
在Rt △AOD中,
????????2=????????2+????????2
即????2=(?????7.23)2+18.52
解得 R=27.3
答:赵州桥的主桥拱的半径约为27.3m.
?
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
连接OA,经过圆心O作OC ⊥AB于D,交AB于C,则C为AB中点,CD就是拱高,
AD=12AB=12×37=18.5,CD=7.23
?
把实际问题转化成数学问题
构造由半径、半弦、弦心距组成的直角三角形
课堂小结
谈谈本节课你的收获吧!
(知识、方法、思想…)
布置作业
习题24.1 第2、8题.
现在,要画出破碎镜片原来的形状,你们有什么想法吗?镜片给你们,请你们课下尝试帮助我.
谢谢!
板书设计
24.1.2垂直于弦的直径
1.圆是轴对称图形,每条直径
所在的直线都是它的对称轴.
2.垂径定理:
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
∵CD为直径,CD⊥AB
∴EA=EB,
3.推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵CD是直径,AE=BE
∴CD⊥AB, AC=BC,AD=BD.
AC=BC,AD=BD.
平分弦的直径垂直于弦,并且
平分弦所对的两条弧.(×)
滑县道口镇第一初中 张海英
义务教育教科书
人教版九年级 上册
帮助老师解决问题:
1.老师有一张圆形纸片,却找不准它的圆心,你们能帮我找到它的圆心吗?
2.老师放在办公桌上的一个圆形小镜子,不小心打破了,你们能用破碎的镜片画出镜子原来的圆形吗?
怎么找圆心?
把圆形纸片对折两次,两次折痕交点即为圆心.
通过折叠,我们发现,圆是_________图形,
_______________________都是圆的对称轴.
轴对称
任何一条直径所在的直线
(如图,AB是⊙0的一条弦, CD是⊙0直径)
我们能不能通过改变AB的位置,
使它成为轴对称图形?
下面这个图形是轴对称图形吗?
在你的圆形纸片上画出改变位置后的图形,并尝试折叠验证.
AB改变位置后的轴对称图形
通过刚才的折叠,你能在
直径CD垂直于弦AB的图中找到
相等的线段有_________________,
相等的弧有_________________.
垂直于弦的直径平分弦,且平分弦所对的两条弧.
让咱们尝试用命题的形式表述这个几何事实:
AE=BE,OC=OD
垂直于弦的直径
直径CD垂直于弦AB
翻折圆.gsp
AC=BC,AD=BD
证明:连接OA、OB
∴沿直线CD折叠,则点A、点B能够重合,
在△OAB中,
∵OA=OB,CD⊥AB,
∴AE=BE,即CD垂直平分AB,
也即点A、点B关于直线CD对称,
进而,AC=BC,AD=BD
垂径定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
定理的符号语言:
∵CD为直径,CD⊥AB
所以,垂径定理常常被用来证明
线段相等、弧相等.
∴EA=EB,AC =BC,AD=BD
小试牛刀
判断下列图形是否都能使用垂径定理?
归纳:定理中的垂径可以是直径、半径、弦心距等过圆心的直线或线段.
回味定理
条件 结论
垂径定理中涉及的这五个内容分别标号为
①经过圆心, ③平分弦,
④平分弦所对的优弧,
②垂直于理弦, ⑤平分弦所对的劣弧.
CD为直径
CD⊥AB
CD平分弦AB
CD平分弧ADB
CD平分弧ACB
平分弦的直径垂直于弦,并且平分弦所对的两条弧.
(×)
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
回味定理
条件 结论
①经过圆心, ③平分弦,
④平分弦所对的优弧,
②垂直于弦, ⑤平分弦所对的劣弧.
圆对称性分析.gsp
CD为直径
CD⊥AB
CD平分弦AB
CD平分弧ADB
CD平分弧ACB
弦的垂直平分线_____________________________
必过圆心,并且平分弦所对的两条弧.
一显身手
1.如图,AB是⊙0的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BC
2.看图填空:
(1)∵ AB是直径,AB⊥CD
∴ _________________________
(2)∵AB是直径, CE=DE
∴ ___________________________
(3)∵ CE=DE,AB⊥CD
∴ _______________________________
C
CE=DE,AC=AD,BC=BD.
AB⊥CD,AC=AD,BC=BD.
AB经过圆心,AC=AD,BC=BD.
3.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点,求证:AC=BD
添加辅助线,构造垂径定理的基本图形.
证明:作OE⊥AB于E,
则AE=BE,CE=DE
∴ AE-CE=BE-DE
即AC=BD
E
4.如图,在⊙0中,弦AB的长为8cm,圆心O到AB的距离为3cm.求⊙0的半径.
归纳:在圆中,我们常常添加的辅助线是弦心距或半径,构造由半径、半弦、弦心距组成的直角三角形,然后再使用勾股定理解决问题.
解:连接OA,作OE ⊥AB于E,
则AE=12AB=12×8=4.
在Rt △AOE中,
OA=????????2+????????2=32+42=5
答:⊙0的半径为5cm.
?
5.自学课本第82页 例2 赵州桥问题
OD=OC-CD=R-7.23
在Rt △AOD中,
????????2=????????2+????????2
即????2=(?????7.23)2+18.52
解得 R=27.3
答:赵州桥的主桥拱的半径约为27.3m.
?
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
连接OA,经过圆心O作OC ⊥AB于D,交AB于C,则C为AB中点,CD就是拱高,
AD=12AB=12×37=18.5,CD=7.23
?
把实际问题转化成数学问题
构造由半径、半弦、弦心距组成的直角三角形
课堂小结
谈谈本节课你的收获吧!
(知识、方法、思想…)
布置作业
习题24.1 第2、8题.
现在,要画出破碎镜片原来的形状,你们有什么想法吗?镜片给你们,请你们课下尝试帮助我.
谢谢!
板书设计
24.1.2垂直于弦的直径
1.圆是轴对称图形,每条直径
所在的直线都是它的对称轴.
2.垂径定理:
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
∵CD为直径,CD⊥AB
∴EA=EB,
3.推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵CD是直径,AE=BE
∴CD⊥AB, AC=BC,AD=BD.
AC=BC,AD=BD.
平分弦的直径垂直于弦,并且
平分弦所对的两条弧.(×)
同课章节目录
