人教版数学九年级上册23.1 图形的旋转 同步上课课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级上册23.1 图形的旋转 同步上课课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 20:24:10 | ||
图片预览




文档简介
23.1 图形的旋转
行唐二中 刘华
自转与公转
认识旋转
探究性质
归纳总结
知识应用
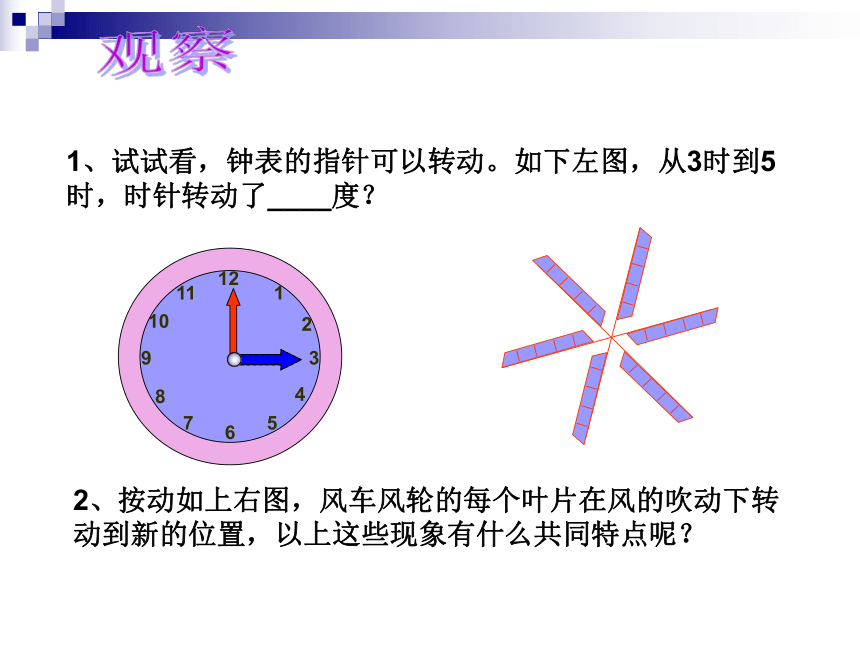
1、试试看,钟表的指针可以转动。如下左图,从3时到5时,时针转动了____度?
2、按动如上右图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
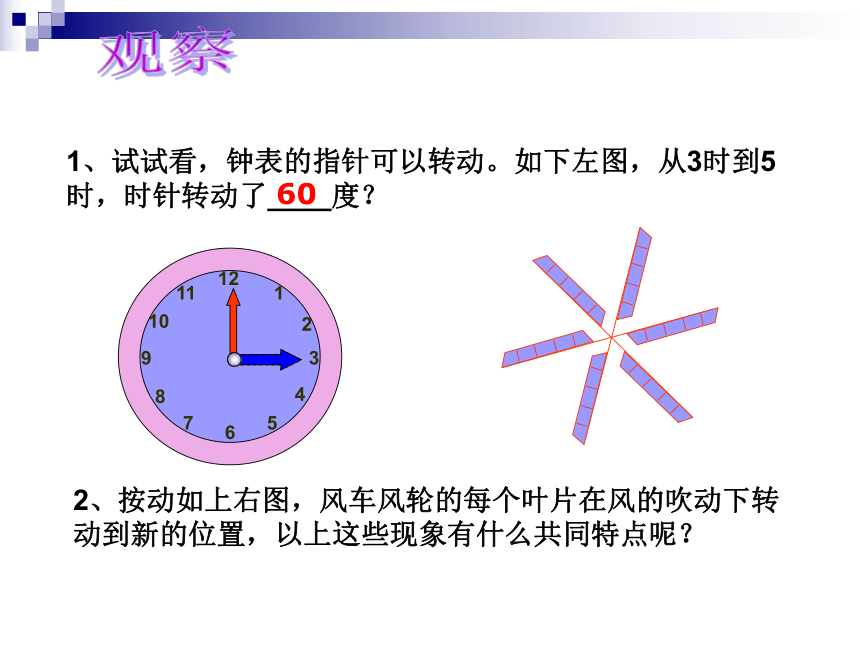
1、试试看,钟表的指针可以转动。如下左图,从3时到5时,时针转动了____度?
2、按动如上右图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
60
12
6
1
2
3
4
5
7
8
9
10
11
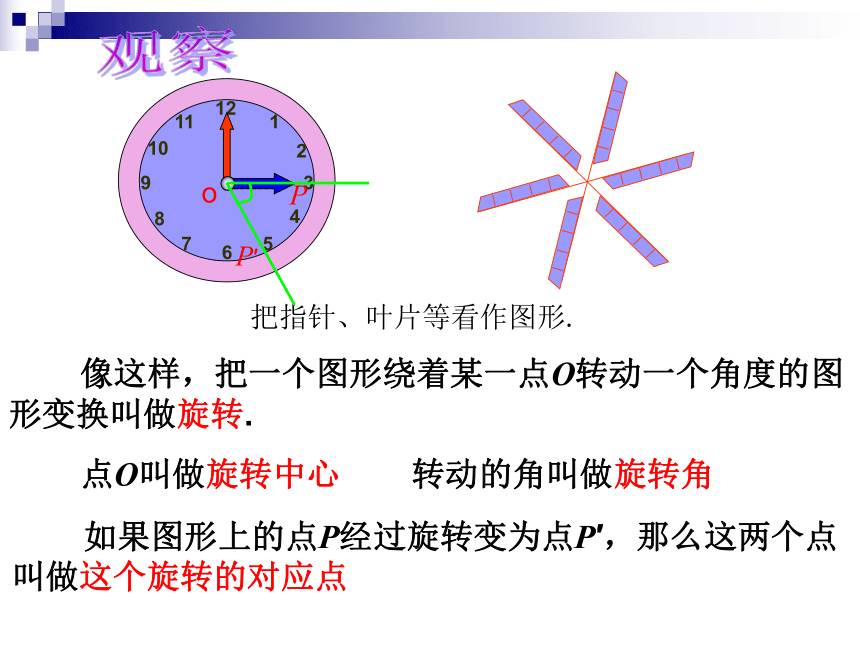
像这样,把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.
把指针、叶片等看作图形.
点O叫做旋转中心
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点
o
P
P′
转动的角叫做旋转角
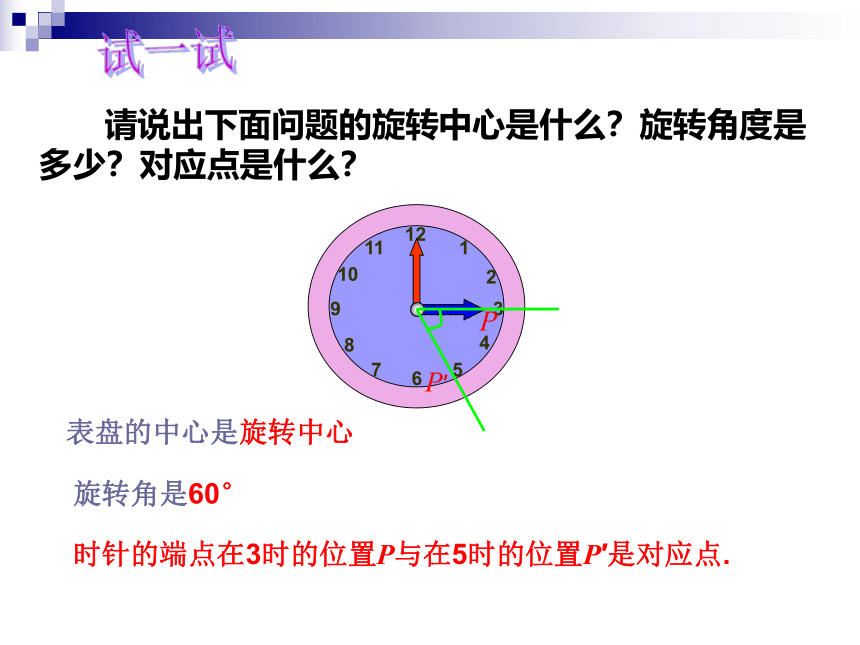
时针的端点在3时的位置P与在5时的位置P′是对应点.
12
6
1
2
3
4
5
7
8
9
10
11
P
P′
请说出下面问题的旋转中心是什么?旋转角度是多少?对应点是什么?
表盘的中心是旋转中心
旋转角是60°
1.举出一些现实生活中旋转的实例,并指出旋转中心和旋转角.
2. 时钟的时针在不停地旋转,从上午6时到上午9时,时针的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
在支点O
旋转角为∠AOA/ 或 ∠BOB/
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
在支点O
旋转角为∠AOA/ 或 ∠BOB/
在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC)然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′) ,移开硬纸板。
思考:线段OA与OA′有什么关系?
∠AOA′与∠BOB′有什么关系?
△ABC与△A′B′C′形状和大小有什么关系?
A
B
C
O
A′
B′
C′
OA=OA′
∠AOA′= ∠BOB′
△ABC≌△A′B′ C′
探究
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
A
B
C
D
E
E′
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
解:因为点A是旋转中心,所以它的对应点是
它本身。
正方形ABCD中,AD=AB ,∠DAB=90°, 所以旋转后点D与B重合.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′= ∠ADE=90°,BE′=DE
还有别的方法吗?
1.如图,小明坐在秋千上,秋千旋转了80°。请在图中小明身上任意选一点P,利用旋转性质,标出点P 的对应点.
P
P′
2.如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
3.找出图中扳手拧螺母时的旋转中心和旋转角。
O
旋转中心为螺母的中心
旋转角为∠POP′
P
P′
3.找出图中扳手拧螺母时的旋转中心和旋转角。
O
旋转中心为螺母的中心
旋转角为∠POP′
P
P′
小结:
对比平移、轴对称两种图形变换,旋转变换与另两种变换有哪些共性与区别?
下列各组图形,可经旋转变换由一个图形得到另一个图形的是( )
A B C D
课后,请设计一个绕一点旋转60°后能与自身重合的图形 。
利用旋转我们还可以进行漂亮的图案设计……
行唐二中 刘华
自转与公转
认识旋转
探究性质
归纳总结
知识应用
1、试试看,钟表的指针可以转动。如下左图,从3时到5时,时针转动了____度?
2、按动如上右图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
1、试试看,钟表的指针可以转动。如下左图,从3时到5时,时针转动了____度?
2、按动如上右图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
60
12
6
1
2
3
4
5
7
8
9
10
11
像这样,把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.
把指针、叶片等看作图形.
点O叫做旋转中心
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点
o
P
P′
转动的角叫做旋转角
时针的端点在3时的位置P与在5时的位置P′是对应点.
12
6
1
2
3
4
5
7
8
9
10
11
P
P′
请说出下面问题的旋转中心是什么?旋转角度是多少?对应点是什么?
表盘的中心是旋转中心
旋转角是60°
1.举出一些现实生活中旋转的实例,并指出旋转中心和旋转角.
2. 时钟的时针在不停地旋转,从上午6时到上午9时,时针的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
在支点O
旋转角为∠AOA/ 或 ∠BOB/
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
在支点O
旋转角为∠AOA/ 或 ∠BOB/
在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC)然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′) ,移开硬纸板。
思考:线段OA与OA′有什么关系?
∠AOA′与∠BOB′有什么关系?
△ABC与△A′B′C′形状和大小有什么关系?
A
B
C
O
A′
B′
C′
OA=OA′
∠AOA′= ∠BOB′
△ABC≌△A′B′ C′
探究
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
A
B
C
D
E
E′
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
解:因为点A是旋转中心,所以它的对应点是
它本身。
正方形ABCD中,AD=AB ,∠DAB=90°, 所以旋转后点D与B重合.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′= ∠ADE=90°,BE′=DE
还有别的方法吗?
1.如图,小明坐在秋千上,秋千旋转了80°。请在图中小明身上任意选一点P,利用旋转性质,标出点P 的对应点.
P
P′
2.如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
3.找出图中扳手拧螺母时的旋转中心和旋转角。
O
旋转中心为螺母的中心
旋转角为∠POP′
P
P′
3.找出图中扳手拧螺母时的旋转中心和旋转角。
O
旋转中心为螺母的中心
旋转角为∠POP′
P
P′
小结:
对比平移、轴对称两种图形变换,旋转变换与另两种变换有哪些共性与区别?
下列各组图形,可经旋转变换由一个图形得到另一个图形的是( )
A B C D
课后,请设计一个绕一点旋转60°后能与自身重合的图形 。
利用旋转我们还可以进行漂亮的图案设计……
同课章节目录
