人教版数学九年级上册23.2.1 中心对称课件(25张ppt)
文档属性
| 名称 | 人教版数学九年级上册23.2.1 中心对称课件(25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 20:27:13 | ||
图片预览






文档简介
23.2.2 中心对称图形
生活中有许多美丽的图案
你发现了吗?
请你欣赏
创设情境
o
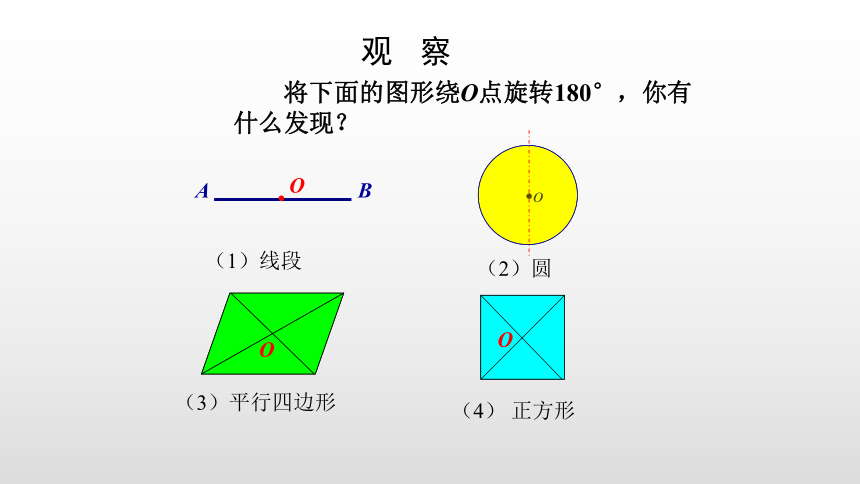
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
观 察
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
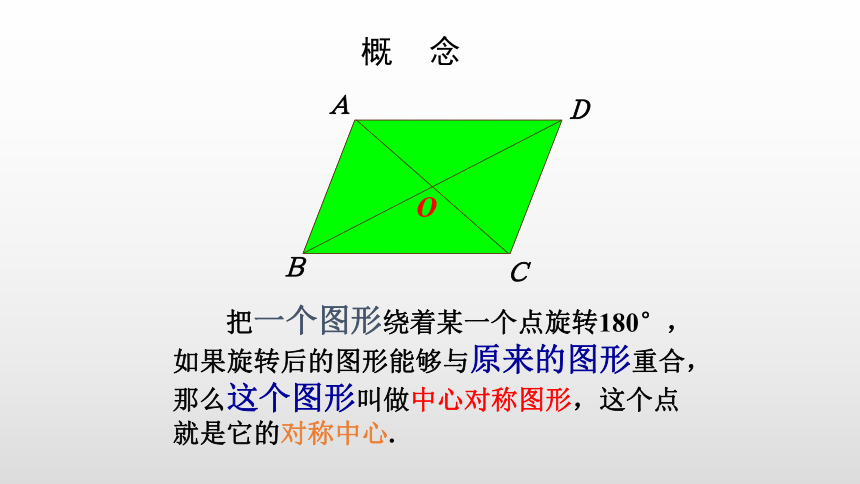
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
C
D
O
概 念
下列图形是中心对称图形吗?
等边三角形不是中心对称图形!
O
讨论:一个中心对称图形有多少个对称中心?
理性提升
1、直线无数个对称中心
2、其它中心对称图形只有一个对称中心。
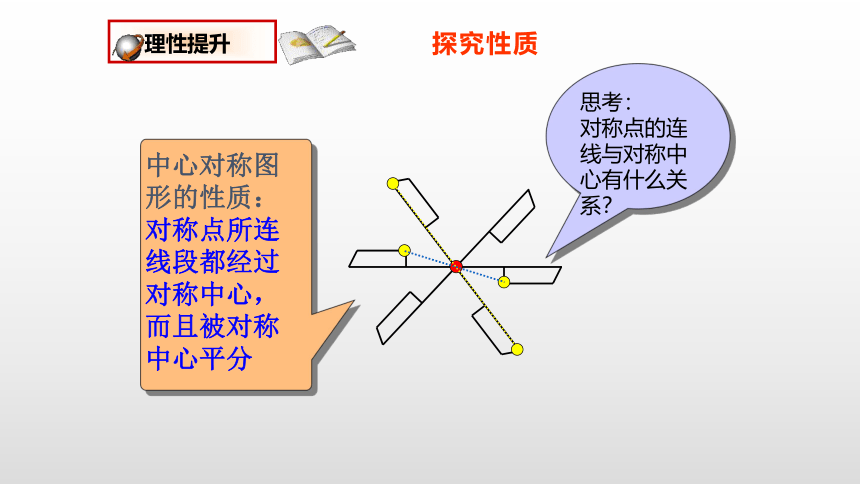
思考:
对称点的连线与对称中心有什么关系?
中心对称图形的性质:
对称点所连线段都经过对称中心,而且被对称中心平分
探究性质
理性提升
F
E
D
C
B
A
一个中心对称图形中对称点连线的交点或对称点连线的中点就是对称中心
理性提升
思考:根据性质,我们可以利用什么方法找对称中心?
中心对称与中心对称图形是两个既有联系又有
区别的概念
区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形
如果将中心对称图形,把对称的部分看成两个图形,则它们是关于中心对称。
对比1
理性提升
轴对称图形与中心对称图形:
轴对称图形
中心对称图形
对称轴——直线
对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图形重合
对比2
理性提升
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩行
菱行
正方形
轴对称图形与中心对称图形的比较
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
2条
中点
角
1条
等腰三角形
1条
等边三角形
3条
平行四边形
对角线交点
矩行
2条
对角线交点
菱行
2条
对角线交点
正方形
4条
对角线交点
轴对称图形与中心对称图形的比较
1.通过旋转平行四边形,你能验证平行四边形的哪些性质?
90度或其整数倍
平行四边形对边相等、对角相等、对角线互相平分.
正方形的四边相等、四角相等、对角线垂直平分且相等.
议一议
2.正方形是中心对称图形吗?
是!
正方形绕两条对角线的交点旋转多少度 能与原来的图形重合?
能由此验证正方形的一些特殊性质吗?
1.我们学过的菱形、矩形、正方形、等腰梯形、
正三角形也都是中心对称图形吗?
2.还有哪些多边形是中心对称图形呢?
结论:中心对称的多边形很多,如边数为偶数的
正多边形都是中心对称图形.
想一想
这些图形是中心对称图形的有( )
——————————————————
⑹
⑺
⑽
⑶
⑴
⑸
⑹
⑷
⑻
⑾
⑿
⑺
⑸
⑼
⑽
⑼
⑿
练一练
这些图形中既是中心对称图形又是轴对称图形的是__________.
A
B
C
F
E
D
B、
D
1、在一次游戏当中,小明将图1的四张扑克牌中的一张旋转180O后,得到图2,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
图1
图2
旋转了方块J,因为其它三张均不是中心对称图形,若旋转了就和会图1不同,而方块J即使旋转了也和图1相同.
随堂练习
A B C E S O W N I x Y Z
2、下列这些字母中有_____个是中心对称的图形.
下列这些数字中有_____个是中心对称的图形.
有_____个是轴对称的图形.
有_____个是轴对称的图形.
6
9
5
4
随堂练习
中考链接
1.
B
C
你知道日常生活中还有哪些轴对称和中心对称图形吗?
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.
一石激起千层浪
你认识这些名车标志吗?
宝马
阿尔法. 罗米欧
奥迪
重庆长安
反思
1.回顾本节课的活动过程.
2.本节课学到了哪些知识?
——应用
(2)中心对称图形的应用
观察
——分析
——探索
——概括
(1)中心对称图形的定义与性质
生活中有许多美丽的图案
你发现了吗?
请你欣赏
创设情境
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
观 察
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
C
D
O
概 念
下列图形是中心对称图形吗?
等边三角形不是中心对称图形!
O
讨论:一个中心对称图形有多少个对称中心?
理性提升
1、直线无数个对称中心
2、其它中心对称图形只有一个对称中心。
思考:
对称点的连线与对称中心有什么关系?
中心对称图形的性质:
对称点所连线段都经过对称中心,而且被对称中心平分
探究性质
理性提升
F
E
D
C
B
A
一个中心对称图形中对称点连线的交点或对称点连线的中点就是对称中心
理性提升
思考:根据性质,我们可以利用什么方法找对称中心?
中心对称与中心对称图形是两个既有联系又有
区别的概念
区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形
如果将中心对称图形,把对称的部分看成两个图形,则它们是关于中心对称。
对比1
理性提升
轴对称图形与中心对称图形:
轴对称图形
中心对称图形
对称轴——直线
对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图形重合
对比2
理性提升
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩行
菱行
正方形
轴对称图形与中心对称图形的比较
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
2条
中点
角
1条
等腰三角形
1条
等边三角形
3条
平行四边形
对角线交点
矩行
2条
对角线交点
菱行
2条
对角线交点
正方形
4条
对角线交点
轴对称图形与中心对称图形的比较
1.通过旋转平行四边形,你能验证平行四边形的哪些性质?
90度或其整数倍
平行四边形对边相等、对角相等、对角线互相平分.
正方形的四边相等、四角相等、对角线垂直平分且相等.
议一议
2.正方形是中心对称图形吗?
是!
正方形绕两条对角线的交点旋转多少度 能与原来的图形重合?
能由此验证正方形的一些特殊性质吗?
1.我们学过的菱形、矩形、正方形、等腰梯形、
正三角形也都是中心对称图形吗?
2.还有哪些多边形是中心对称图形呢?
结论:中心对称的多边形很多,如边数为偶数的
正多边形都是中心对称图形.
想一想
这些图形是中心对称图形的有( )
——————————————————
⑹
⑺
⑽
⑶
⑴
⑸
⑹
⑷
⑻
⑾
⑿
⑺
⑸
⑼
⑽
⑼
⑿
练一练
这些图形中既是中心对称图形又是轴对称图形的是__________.
A
B
C
F
E
D
B、
D
1、在一次游戏当中,小明将图1的四张扑克牌中的一张旋转180O后,得到图2,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
图1
图2
旋转了方块J,因为其它三张均不是中心对称图形,若旋转了就和会图1不同,而方块J即使旋转了也和图1相同.
随堂练习
A B C E S O W N I x Y Z
2、下列这些字母中有_____个是中心对称的图形.
下列这些数字中有_____个是中心对称的图形.
有_____个是轴对称的图形.
有_____个是轴对称的图形.
6
9
5
4
随堂练习
中考链接
1.
B
C
你知道日常生活中还有哪些轴对称和中心对称图形吗?
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.
一石激起千层浪
你认识这些名车标志吗?
宝马
阿尔法. 罗米欧
奥迪
重庆长安
反思
1.回顾本节课的活动过程.
2.本节课学到了哪些知识?
——应用
(2)中心对称图形的应用
观察
——分析
——探索
——概括
(1)中心对称图形的定义与性质
同课章节目录
