人教版数学九年级上册24.1.2 垂直于弦的直径 教学配套课件(共16张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.2 垂直于弦的直径 教学配套课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览






文档简介
勤奋是进步的阶梯;
思考是超越的基础;
行动是成功的开始。
别人的注释代替不了自己的理解,愿你有所发现,有所创造。
长葛一中 冯伟军
1、知道圆是轴对称图形,每一条过圆心的直线都是它的对称轴。
2、通过动手操作、观察思考,归纳出垂径定理及其推论。
3、会用垂径定理进行与弦有关的简单计算和证明。
如果一个图形沿着一条直线对折,直线两旁的部分能够完全互相重合,那么这个图形叫做 ______对称图形,这条直线叫做它的________ .
2.等腰三角形是轴对称图形,它的对称轴是______________________.
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
圆是轴对称图形,它的对称轴是任意一条直径所在的直线.
发现:
·
O
A
B
C
D
E
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E.
(2)你能发现图中有那些相等的线段和弧?为什么?
(1)此图是轴对称图形吗?如果是,它的对称轴是什么?
弧: AC=BC,AD=BD
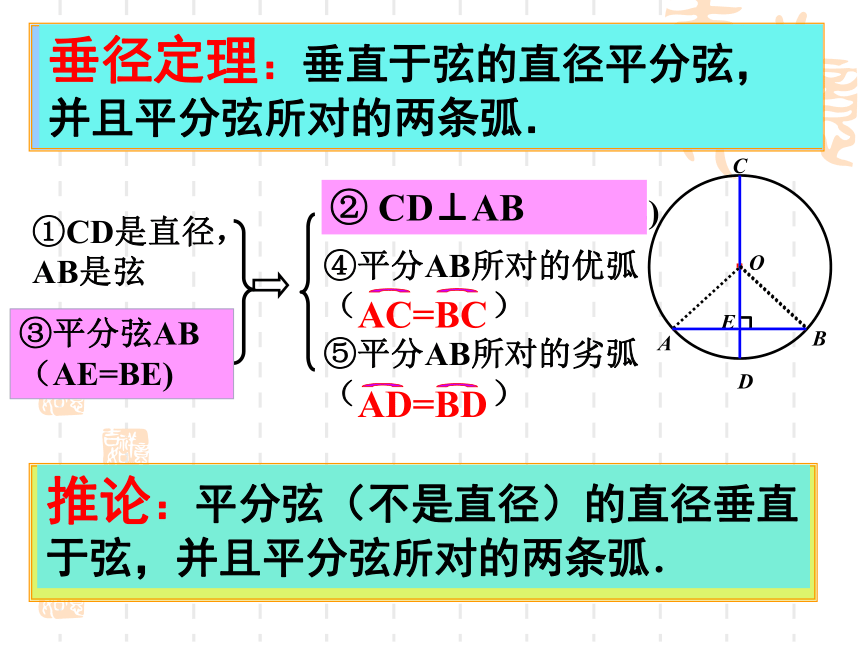
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
①CD是直径,AB是弦
② CD⊥AB
③平分弦AB(AE=BE)
③平分弦AB(AE=BE)
② CD⊥AB
④平分AB所对的优弧( )
AC=BC
⑤平分AB所对的劣弧( )
AD=BD
试一试
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧。
E
O
A
B
D
C
O
B
A
E
E
O
A
B
C
E
O
C
D
A
B
E
A
B
C
D
O
例1已知,如图,在⊙O中,圆心O到AB的距离为3cm ,弦AB的长为8cm. 求: ⊙O的半径.
⊙O的半径为6cm.
弦AB的长.
解:过O 作OE⊥AB,垂足为E,连结OA,
则OE=3cm,∵ ⊥ , ∴AE =BE= AB
∵AB=8cm ∴AE=4cm
在Rt⊿AOE中,根据勾股定理
OA2=OE2+AE2
即 OA2= ,解得 OA = .
∴⊙O的半径为 cm.
OE
AB
32+42
5
5
1
2
A
B
.
O
E
例2 已知如图①:在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
(1)若AB为直径,求证: AC = BD.
(2)若AB为不过圆心的弦(如图②),猜想AC 与 BD的大小关系,并证明。
① ②
E
解: AC=BD
证明:过圆心O作OE⊥AB,垂足为E,∵OE⊥AB
∴AE=BE,CE=DE
∴ AE-CE=BE-DE
即 AC=BD
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,下列结论错误的是( )
·
O
A
B
C
D
E
A.CE=DE; B.
C.OE=BE D.∠COE=∠DOE
2.下列语句错误的是( )
A.垂直于弦的直径平分这条弦 ,且平分弦所对的优弧。
B.垂直于弦的直径平分这条弦 ,且平分弦所对的劣弧。
C.平分弦的直径垂直于这条弦 ,且平分弦所对的优弧。
D.弦的垂直平分线必过圆心。
C
C
BD = BC
O
A
B
D
C
3.在⊙O中,弦AB=12厘米,OC⊥AB于点D,CD=2cm, 求⊙O的半径。
请大家围绕以下两个问题谈谈这节课你有哪些收获?有何体会?
① 垂径定理的内容是 。
② 在圆中解决与弦有关问题时经常作的辅助线是 。
1.如图,在⊙O中,弦AB的长为12cm,圆心O到AB的距离为3cm,求⊙O的半径.
·
O
A
B
E
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E。
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
1.已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,那么过P点的最短的弦长。
2.如图是一个输水管道的横截面,水面宽16米cm,有水部分的最大深度是4cm,求这个圆形截面的半径。
.O
B
A
思考是超越的基础;
行动是成功的开始。
别人的注释代替不了自己的理解,愿你有所发现,有所创造。
长葛一中 冯伟军
1、知道圆是轴对称图形,每一条过圆心的直线都是它的对称轴。
2、通过动手操作、观察思考,归纳出垂径定理及其推论。
3、会用垂径定理进行与弦有关的简单计算和证明。
如果一个图形沿着一条直线对折,直线两旁的部分能够完全互相重合,那么这个图形叫做 ______对称图形,这条直线叫做它的________ .
2.等腰三角形是轴对称图形,它的对称轴是______________________.
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
圆是轴对称图形,它的对称轴是任意一条直径所在的直线.
发现:
·
O
A
B
C
D
E
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E.
(2)你能发现图中有那些相等的线段和弧?为什么?
(1)此图是轴对称图形吗?如果是,它的对称轴是什么?
弧: AC=BC,AD=BD
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
①CD是直径,AB是弦
② CD⊥AB
③平分弦AB(AE=BE)
③平分弦AB(AE=BE)
② CD⊥AB
④平分AB所对的优弧( )
AC=BC
⑤平分AB所对的劣弧( )
AD=BD
试一试
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧。
E
O
A
B
D
C
O
B
A
E
E
O
A
B
C
E
O
C
D
A
B
E
A
B
C
D
O
例1已知,如图,在⊙O中,圆心O到AB的距离为3cm ,弦AB的长为8cm. 求: ⊙O的半径.
⊙O的半径为6cm.
弦AB的长.
解:过O 作OE⊥AB,垂足为E,连结OA,
则OE=3cm,∵ ⊥ , ∴AE =BE= AB
∵AB=8cm ∴AE=4cm
在Rt⊿AOE中,根据勾股定理
OA2=OE2+AE2
即 OA2= ,解得 OA = .
∴⊙O的半径为 cm.
OE
AB
32+42
5
5
1
2
A
B
.
O
E
例2 已知如图①:在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
(1)若AB为直径,求证: AC = BD.
(2)若AB为不过圆心的弦(如图②),猜想AC 与 BD的大小关系,并证明。
① ②
E
解: AC=BD
证明:过圆心O作OE⊥AB,垂足为E,∵OE⊥AB
∴AE=BE,CE=DE
∴ AE-CE=BE-DE
即 AC=BD
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,下列结论错误的是( )
·
O
A
B
C
D
E
A.CE=DE; B.
C.OE=BE D.∠COE=∠DOE
2.下列语句错误的是( )
A.垂直于弦的直径平分这条弦 ,且平分弦所对的优弧。
B.垂直于弦的直径平分这条弦 ,且平分弦所对的劣弧。
C.平分弦的直径垂直于这条弦 ,且平分弦所对的优弧。
D.弦的垂直平分线必过圆心。
C
C
BD = BC
O
A
B
D
C
3.在⊙O中,弦AB=12厘米,OC⊥AB于点D,CD=2cm, 求⊙O的半径。
请大家围绕以下两个问题谈谈这节课你有哪些收获?有何体会?
① 垂径定理的内容是 。
② 在圆中解决与弦有关问题时经常作的辅助线是 。
1.如图,在⊙O中,弦AB的长为12cm,圆心O到AB的距离为3cm,求⊙O的半径.
·
O
A
B
E
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E。
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
1.已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,那么过P点的最短的弦长。
2.如图是一个输水管道的横截面,水面宽16米cm,有水部分的最大深度是4cm,求这个圆形截面的半径。
.O
B
A
同课章节目录
