人教版数学九年级上册24.3.1 正多边形和圆 经典课件(共34张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.3.1 正多边形和圆 经典课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览




文档简介
24.3正多边形和圆
观察下列图形他们有什么特点?
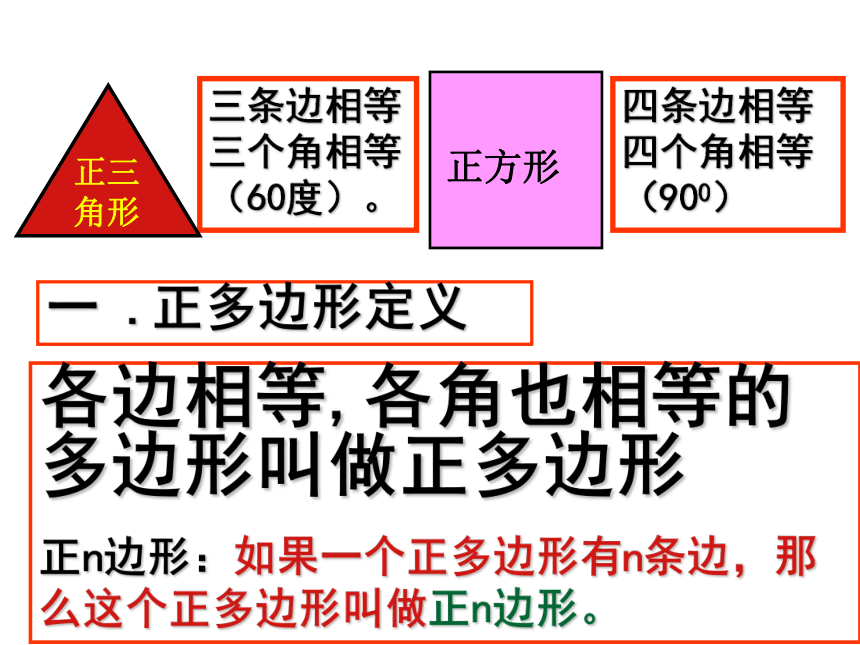
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
各边相等,各角也相等的多边形叫做正多边形
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
一 .正多边形定义
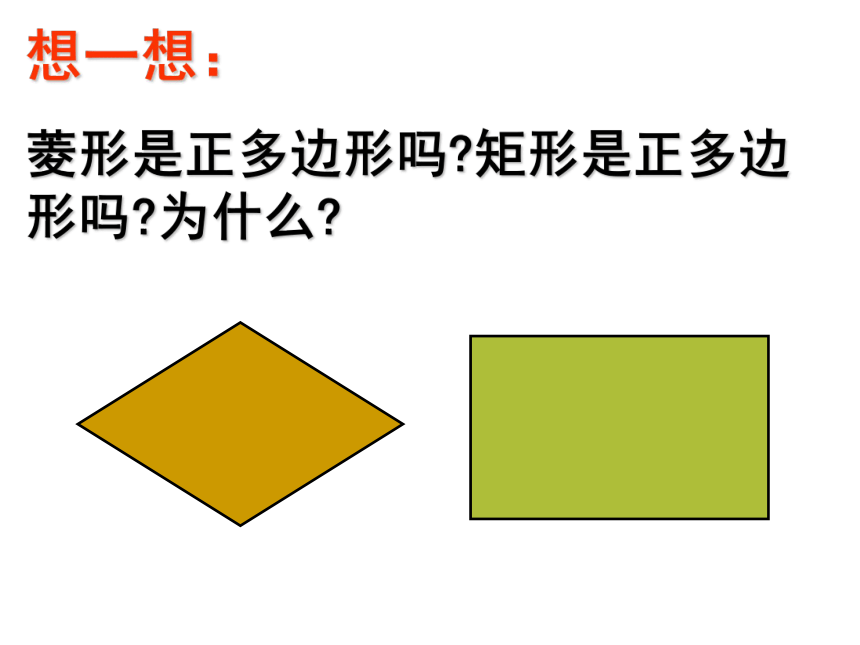
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
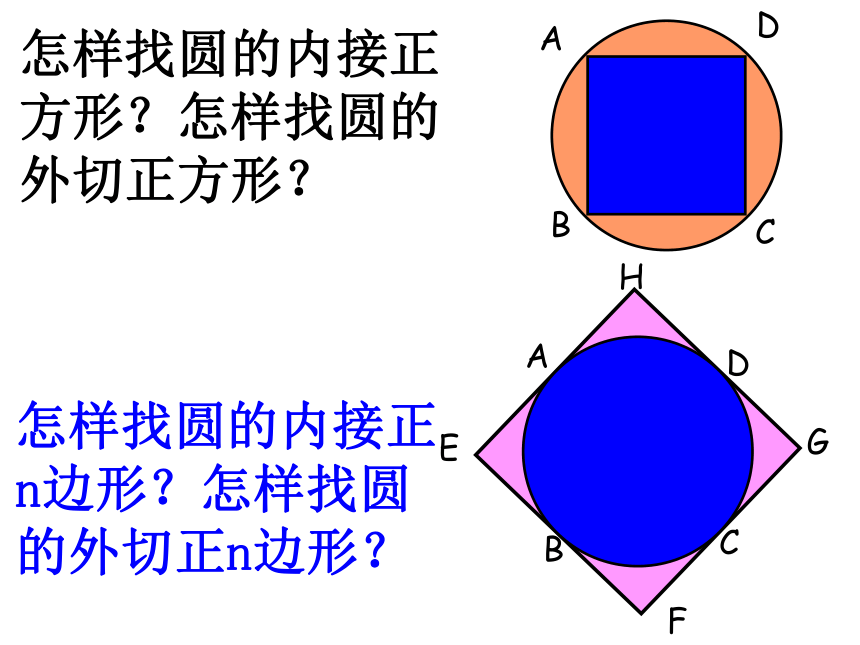
怎样找圆的内接正方形?怎样找圆的外切正方形?
怎样找圆的内接正n边形?怎样找圆的外切正n边形?
E
F
G
H
A
B
C
D
A
B
C
D
定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正多边形。
正n边形与圆有密切的关系
把正n边形的边数无限增多,就接近于圆.
E
F
C
D
.
O
中心角
半径R
边心距r
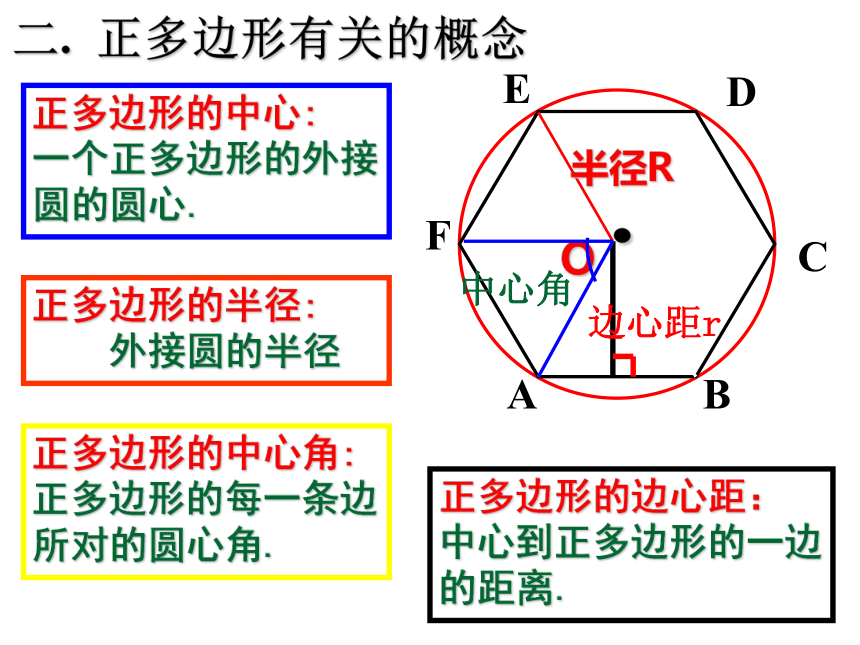
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
二. 正多边形有关的概念
B
A
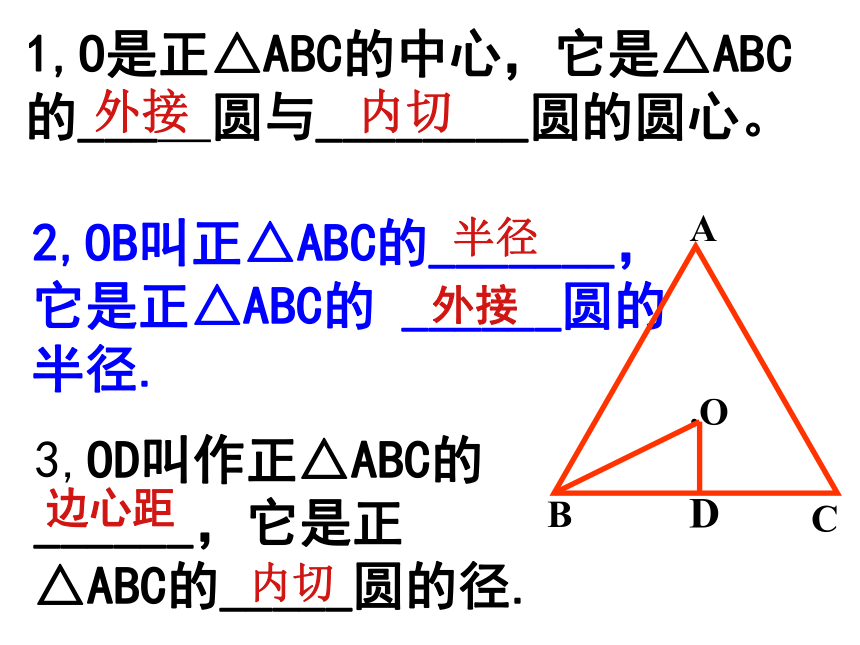
1,O是正△ABC的中心,它是△ABC的___ 圆与________圆的圆心。
2,OB叫正△ABC的_______,它是正△ABC的 ______圆的半径.
3,OD叫作正△ABC的______,它是正△ABC的_____圆的径.
A
B
C
.O
D
外接
内切
半径
外接
边心距
内切
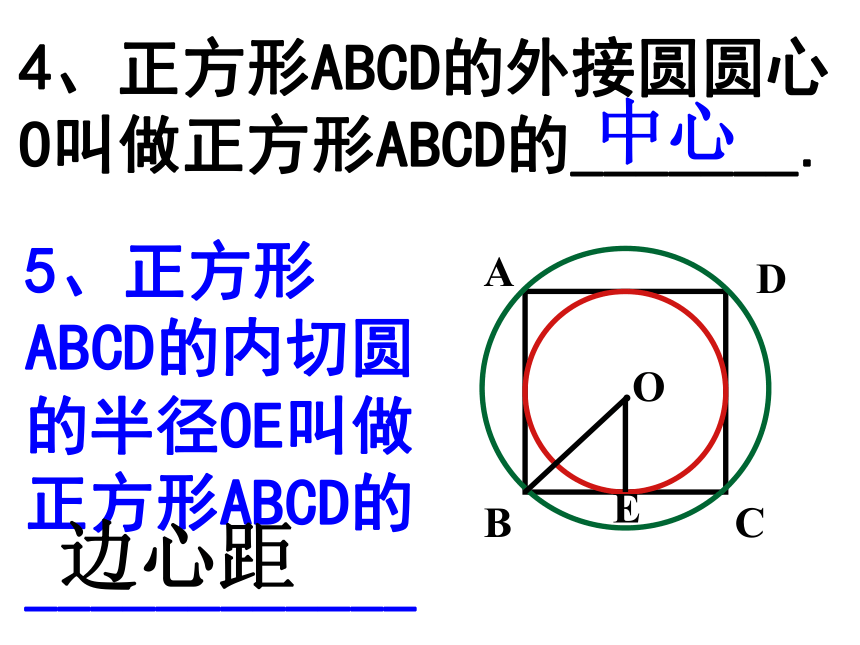
4、正方形ABCD的外接圆圆心O叫做正方形ABCD的_______.
5、正方形ABCD的内切圆的半径OE叫做正方形ABCD的____________
A
B
C
D
.O
E
中心
边心距
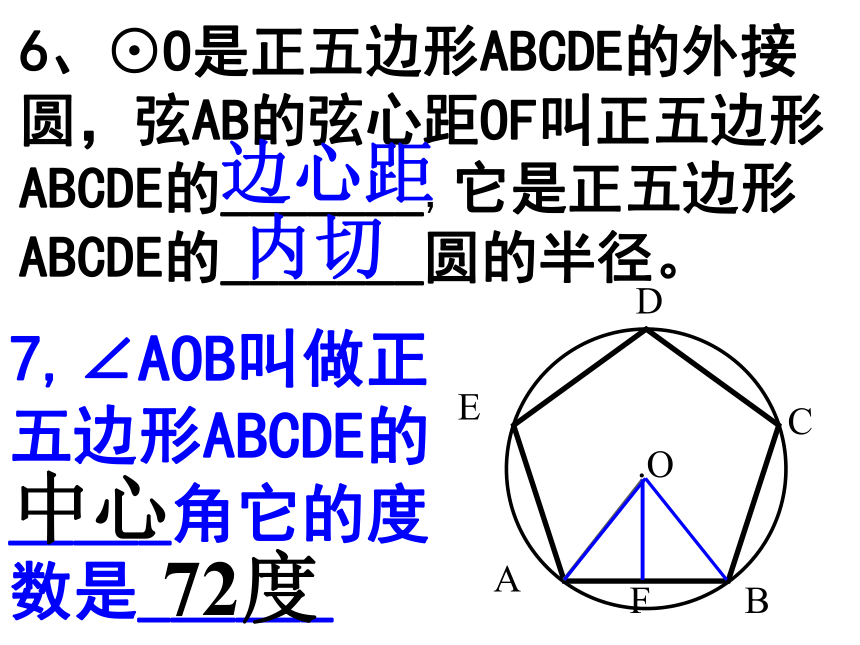
6、⊙O是正五边形ABCDE的外接圆,弦AB的弦心距OF叫正五边形ABCDE的_______,它是正五边形ABCDE的_______圆的半径。
7,∠AOB叫做正五边形ABCDE的_____角它的度数是______
D
E
A
B
C
.O
F
边心距
内切
中心
72度
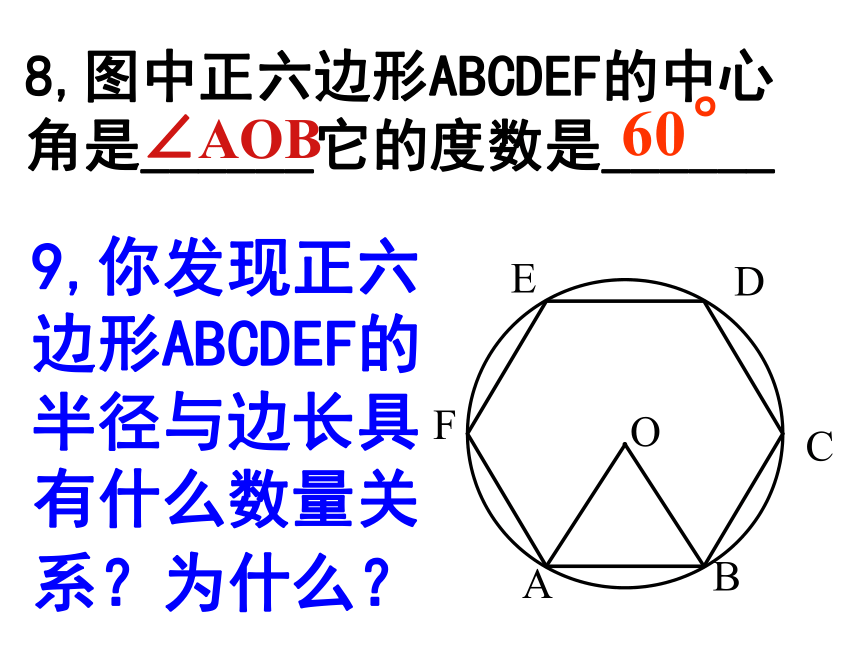
8,图中正六边形ABCDEF的中心角是______它的度数是______
9,你发现正六边形ABCDEF的半径与边长具有什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
1、判断题。
①各边都相等的多边形是正多边形。( )
②一个圆有且只有一个内接正多边形( )
×
×
求证:正五边形的对角线相等.
A
B
C
D
E
已知:ABCDE是正五边形,求证:DB=CE
正多边形的有关计算
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
定理
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆。
正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,内切圆的半径叫做正多边形的边心距。正多边形各边所对的外接圆的圆心角叫做正多边形的中心角。正n边形的每个中心角都等于360°/n。
讨论:正n边形的一个内角等于_____度,中心角等于__________
一个外角等于__________
F
A
D
E
.
C
B
例 有一个亭子它的地基是半径为4m的正六边形
求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
∴亭子的周长 L=6×4=24(m)
F
A
D
E
.
.
O
B
C
r
R=4
P
正多边形对称性
1、正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
2、边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。
两个正六边形的边长分别是3和4,这两个正六边形的面积之比等于_______
圆内接正方形的半径与边长的比值是________
圆内接正四边形的边长为4cm,那么边心距是_______
已知圆内接正方形的边长为4,则该圆的内接正六边形边长为__________.
圆内接正六边形的边长是8 cm用么该正六边形的半径为____,边心距_____.
正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补
C.互余或互补 D.不能确定
正多边形的性质
各边相等,各角相等
圆的内接正n边形的各个顶点把圆分成n等分
圆的外切正n边形的各边与圆的n个切点把圆分成n等分
每个正多边形都有一个内切圆和外接圆,这两个圆是同心圆,圆心就是正多边形的中心
正多边形都是轴对称图形,如果边数是偶数那么它还是中心对称图形
正n边形的中心角和它的每个外角都等于360°/n,每个内角都等于(n-2)·180°/n
边数相同的正多边形相似,周长比、边长比、半径比、边心距比、对应对角线比都等于相似比,面积比等于相似比平方
求证:各边相等的圆内接多边形是正多边形。
求证:各角相等的圆外切多边形是正多边形。
思考:
各边相等的圆外切多边形是否是正多边形?
各角相等的圆内接多边形是否是正多边形?
下列图形中:①正五边形;②等腰三角形;③正八边形;④正2n(n为自然数)边形;⑤任意的平行四边形。是轴对称图形的有__________,是中心对称图形的有________,既是中心对称图形,又是轴对称图形的有_______。
①②③④
③④⑤
③④
已知正三角形ABC的边长为4,则它的内切圆和外接圆组成的圆环面积是多少?
D
O
C
A
B
A、B、C在⊙O上,且B在弧AC上,AB、AC分别是正九边形和正六边形的一边。请问:BC是此圆内接正几边形的一边?
观察下列图形他们有什么特点?
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
各边相等,各角也相等的多边形叫做正多边形
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
一 .正多边形定义
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
怎样找圆的内接正方形?怎样找圆的外切正方形?
怎样找圆的内接正n边形?怎样找圆的外切正n边形?
E
F
G
H
A
B
C
D
A
B
C
D
定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正多边形。
正n边形与圆有密切的关系
把正n边形的边数无限增多,就接近于圆.
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
二. 正多边形有关的概念
B
A
1,O是正△ABC的中心,它是△ABC的___ 圆与________圆的圆心。
2,OB叫正△ABC的_______,它是正△ABC的 ______圆的半径.
3,OD叫作正△ABC的______,它是正△ABC的_____圆的径.
A
B
C
.O
D
外接
内切
半径
外接
边心距
内切
4、正方形ABCD的外接圆圆心O叫做正方形ABCD的_______.
5、正方形ABCD的内切圆的半径OE叫做正方形ABCD的____________
A
B
C
D
.O
E
中心
边心距
6、⊙O是正五边形ABCDE的外接圆,弦AB的弦心距OF叫正五边形ABCDE的_______,它是正五边形ABCDE的_______圆的半径。
7,∠AOB叫做正五边形ABCDE的_____角它的度数是______
D
E
A
B
C
.O
F
边心距
内切
中心
72度
8,图中正六边形ABCDEF的中心角是______它的度数是______
9,你发现正六边形ABCDEF的半径与边长具有什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
1、判断题。
①各边都相等的多边形是正多边形。( )
②一个圆有且只有一个内接正多边形( )
×
×
求证:正五边形的对角线相等.
A
B
C
D
E
已知:ABCDE是正五边形,求证:DB=CE
正多边形的有关计算
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
定理
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆。
正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,内切圆的半径叫做正多边形的边心距。正多边形各边所对的外接圆的圆心角叫做正多边形的中心角。正n边形的每个中心角都等于360°/n。
讨论:正n边形的一个内角等于_____度,中心角等于__________
一个外角等于__________
F
A
D
E
.
C
B
例 有一个亭子它的地基是半径为4m的正六边形
求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
∴亭子的周长 L=6×4=24(m)
F
A
D
E
.
.
O
B
C
r
R=4
P
正多边形对称性
1、正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
2、边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。
两个正六边形的边长分别是3和4,这两个正六边形的面积之比等于_______
圆内接正方形的半径与边长的比值是________
圆内接正四边形的边长为4cm,那么边心距是_______
已知圆内接正方形的边长为4,则该圆的内接正六边形边长为__________.
圆内接正六边形的边长是8 cm用么该正六边形的半径为____,边心距_____.
正多边形的中心角与该正多边形一个内角的关系是( )
A.互余 B.互补
C.互余或互补 D.不能确定
正多边形的性质
各边相等,各角相等
圆的内接正n边形的各个顶点把圆分成n等分
圆的外切正n边形的各边与圆的n个切点把圆分成n等分
每个正多边形都有一个内切圆和外接圆,这两个圆是同心圆,圆心就是正多边形的中心
正多边形都是轴对称图形,如果边数是偶数那么它还是中心对称图形
正n边形的中心角和它的每个外角都等于360°/n,每个内角都等于(n-2)·180°/n
边数相同的正多边形相似,周长比、边长比、半径比、边心距比、对应对角线比都等于相似比,面积比等于相似比平方
求证:各边相等的圆内接多边形是正多边形。
求证:各角相等的圆外切多边形是正多边形。
思考:
各边相等的圆外切多边形是否是正多边形?
各角相等的圆内接多边形是否是正多边形?
下列图形中:①正五边形;②等腰三角形;③正八边形;④正2n(n为自然数)边形;⑤任意的平行四边形。是轴对称图形的有__________,是中心对称图形的有________,既是中心对称图形,又是轴对称图形的有_______。
①②③④
③④⑤
③④
已知正三角形ABC的边长为4,则它的内切圆和外接圆组成的圆环面积是多少?
D
O
C
A
B
A、B、C在⊙O上,且B在弧AC上,AB、AC分别是正九边形和正六边形的一边。请问:BC是此圆内接正几边形的一边?
同课章节目录
