人教版数学九年级上册25.3 用频率估计概率(第1课时)上课课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册25.3 用频率估计概率(第1课时)上课课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 20:39:11 | ||
图片预览






文档简介
25.3 用频率估计概率(第1课时)
用列举法求概率的条件是什么?
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?
买彩票
2.任务1
从1到40的号码中选取一个,买40张彩票一定能中奖吗?
通过计算,40张彩票至少有一张中奖的概率是63.7%,没有一张中奖的概率为36.3%。
抛掷一枚硬币,“正面向上”的概率为 0.5.
这是否意味着:
“抛掷 2 次,1 次正面向上”?
“抛掷 100次,50 次正面向上”?
1.问题引入
棣莫弗
正 面
反 面
2.任务1
活动:
抛掷一枚硬币 100次,统计“正面向上”出现的频数,计算频率,填写表格,思考.
组员分工:
1 号同学 抛掷硬币,约达 1 臂高度,接住落下的
硬币,报告试验结果;
2 号同学 用画记法记录试验结果,监督,尽可能 保证每次试验条件相同,确保试验的随机性,填写表格.
全班同学分成10个小组,同时进行试验.
考察频率与概率是否相同?
{5940675A-B579-460E-94D1-54222C63F5DA} 次数
100
100
100
100
100
100
100
100
100
100
正面向
上次数
正面向
上频率
统 计 表
活动:
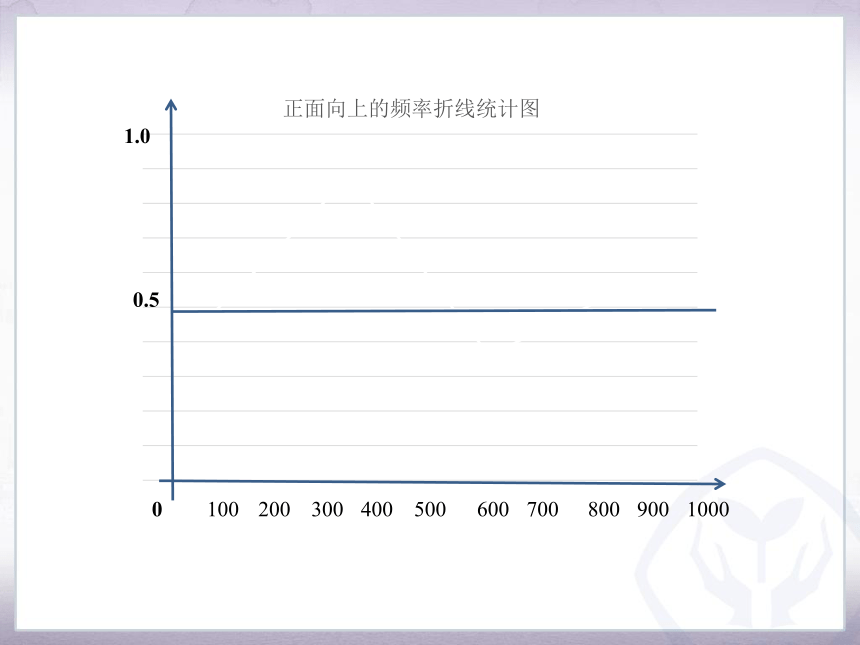
逐步累加各小组试验获得的“正面向上”的频数,求频率,画出频率的折线图,观察、思考.
3.任务2
任务2:观察随着重复试验次数的增加,“正面向上”的频率的变化趋势是什么?
{5940675A-B579-460E-94D1-54222C63F5DA} 次数
100
200
300
400
500
600
700
800
900
1000
正面向
上次数
正面向
上频率
统 计 表
100
200
300
400
500
900
700
800
600
1000
0.5
0
1.0
第一组1 000 次试验
第二组1 000 次试验
试验者
抛掷次数
n
“正面向上”
的次数
m
“正面向上”
的频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
2 048
4 040
10 000
12 000
24 000
1 061
2 048
4 979
6 019
12 012
0.518
0.506 9
0.497 9
0.501 6
0.500 5
历史上,有些人曾做过成千上万次抛掷硬币的试
验,其中一些试验结果见下表:
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
4.归纳方法
用频率估计概率.
雅各布·伯努利
(1654-1705)
孟德尔发现遗传定律
问题:投一个瓶盖,你能估计出“瓶盖朝上”的概率吗?
瓶盖朝上
瓶盖朝下
猜一猜:“瓶盖朝上”可能性与“瓶盖朝下”的可
能性哪个更大?
5.运用方法
用频率估计概率.
活动:抛掷一枚瓶盖1 次,统计“瓶盖朝上”出现的频数,逐步累加全班数据,观察频率变化,估计“瓶盖朝上”的概率.
注意:水平拿瓶盖,如图,从视线高度松手,让瓶盖下落,尽可能保证每次试验条件相同,确保试验的随
机性.
任务2:抛掷一个瓶盖,估计“瓶盖朝上”的概率.
6.任务2
{5940675A-B579-460E-94D1-54222C63F5DA} 组别
1组
2组
3组
4组
5组
6组
7组
8组
9组
10组
瓶盖朝
上次数
瓶盖朝
上频率
{5940675A-B579-460E-94D1-54222C63F5DA} 组别
100
200
300
400
500
600
700
800
900
1000
瓶盖朝
上次数
瓶盖朝
上频率
猜测瓶口朝上概率:
用频率估计瓶口朝上概率为:
?
(1) 下列随机事件,既可以用列表法求得,又可以用频率估计获得的是( )
A、某运动员在某种条件下“射中9环以上”的概率
B、某种幼苗在一定条件下的移植存活率
C、某种柑橘在某运输过程中的损坏率
D、投掷一枚均匀的骰子,朝上一面点数为奇数的概率。
小测试
(2)估计移植成活率
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n)
成活数(m)
10
8
成活的频率
0.8
( )
50
47
270
235
0.870
400
369
750
662
1500
1335
0.890
3500
3203
0.915
7000
6335
9000
8073
14000
12628
0.902
0.94
0.923
0.883
0.905
0.897
(3) 一个不透明口袋里装有除颜色外都相同的5个白球和若干个红球,小亮现将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球,因此小亮估计口袋中的红球大约有( )个。
A.45 B.48 C.50 D.55
小结
用频率估计概率的方法:
1、做大量重复实验
2、统计事件发生的频率
3、用频率估计事件发生的概率
优点:
适用范围更广,对不能用列举法求概率的随机事件,可以通过大量重复实验估计其概率。
《导学案》P121、P122
8.布置作业
用列举法求概率的条件是什么?
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?
买彩票
2.任务1
从1到40的号码中选取一个,买40张彩票一定能中奖吗?
通过计算,40张彩票至少有一张中奖的概率是63.7%,没有一张中奖的概率为36.3%。
抛掷一枚硬币,“正面向上”的概率为 0.5.
这是否意味着:
“抛掷 2 次,1 次正面向上”?
“抛掷 100次,50 次正面向上”?
1.问题引入
棣莫弗
正 面
反 面
2.任务1
活动:
抛掷一枚硬币 100次,统计“正面向上”出现的频数,计算频率,填写表格,思考.
组员分工:
1 号同学 抛掷硬币,约达 1 臂高度,接住落下的
硬币,报告试验结果;
2 号同学 用画记法记录试验结果,监督,尽可能 保证每次试验条件相同,确保试验的随机性,填写表格.
全班同学分成10个小组,同时进行试验.
考察频率与概率是否相同?
{5940675A-B579-460E-94D1-54222C63F5DA} 次数
100
100
100
100
100
100
100
100
100
100
正面向
上次数
正面向
上频率
统 计 表
活动:
逐步累加各小组试验获得的“正面向上”的频数,求频率,画出频率的折线图,观察、思考.
3.任务2
任务2:观察随着重复试验次数的增加,“正面向上”的频率的变化趋势是什么?
{5940675A-B579-460E-94D1-54222C63F5DA} 次数
100
200
300
400
500
600
700
800
900
1000
正面向
上次数
正面向
上频率
统 计 表
100
200
300
400
500
900
700
800
600
1000
0.5
0
1.0
第一组1 000 次试验
第二组1 000 次试验
试验者
抛掷次数
n
“正面向上”
的次数
m
“正面向上”
的频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
2 048
4 040
10 000
12 000
24 000
1 061
2 048
4 979
6 019
12 012
0.518
0.506 9
0.497 9
0.501 6
0.500 5
历史上,有些人曾做过成千上万次抛掷硬币的试
验,其中一些试验结果见下表:
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
4.归纳方法
用频率估计概率.
雅各布·伯努利
(1654-1705)
孟德尔发现遗传定律
问题:投一个瓶盖,你能估计出“瓶盖朝上”的概率吗?
瓶盖朝上
瓶盖朝下
猜一猜:“瓶盖朝上”可能性与“瓶盖朝下”的可
能性哪个更大?
5.运用方法
用频率估计概率.
活动:抛掷一枚瓶盖1 次,统计“瓶盖朝上”出现的频数,逐步累加全班数据,观察频率变化,估计“瓶盖朝上”的概率.
注意:水平拿瓶盖,如图,从视线高度松手,让瓶盖下落,尽可能保证每次试验条件相同,确保试验的随
机性.
任务2:抛掷一个瓶盖,估计“瓶盖朝上”的概率.
6.任务2
{5940675A-B579-460E-94D1-54222C63F5DA} 组别
1组
2组
3组
4组
5组
6组
7组
8组
9组
10组
瓶盖朝
上次数
瓶盖朝
上频率
{5940675A-B579-460E-94D1-54222C63F5DA} 组别
100
200
300
400
500
600
700
800
900
1000
瓶盖朝
上次数
瓶盖朝
上频率
猜测瓶口朝上概率:
用频率估计瓶口朝上概率为:
?
(1) 下列随机事件,既可以用列表法求得,又可以用频率估计获得的是( )
A、某运动员在某种条件下“射中9环以上”的概率
B、某种幼苗在一定条件下的移植存活率
C、某种柑橘在某运输过程中的损坏率
D、投掷一枚均匀的骰子,朝上一面点数为奇数的概率。
小测试
(2)估计移植成活率
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n)
成活数(m)
10
8
成活的频率
0.8
( )
50
47
270
235
0.870
400
369
750
662
1500
1335
0.890
3500
3203
0.915
7000
6335
9000
8073
14000
12628
0.902
0.94
0.923
0.883
0.905
0.897
(3) 一个不透明口袋里装有除颜色外都相同的5个白球和若干个红球,小亮现将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球,因此小亮估计口袋中的红球大约有( )个。
A.45 B.48 C.50 D.55
小结
用频率估计概率的方法:
1、做大量重复实验
2、统计事件发生的频率
3、用频率估计事件发生的概率
优点:
适用范围更广,对不能用列举法求概率的随机事件,可以通过大量重复实验估计其概率。
《导学案》P121、P122
8.布置作业
同课章节目录
