人教版数学七年级下册 8.2.1代入消元法解二元一次方程组课件(共15张)
文档属性
| 名称 | 人教版数学七年级下册 8.2.1代入消元法解二元一次方程组课件(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 807.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




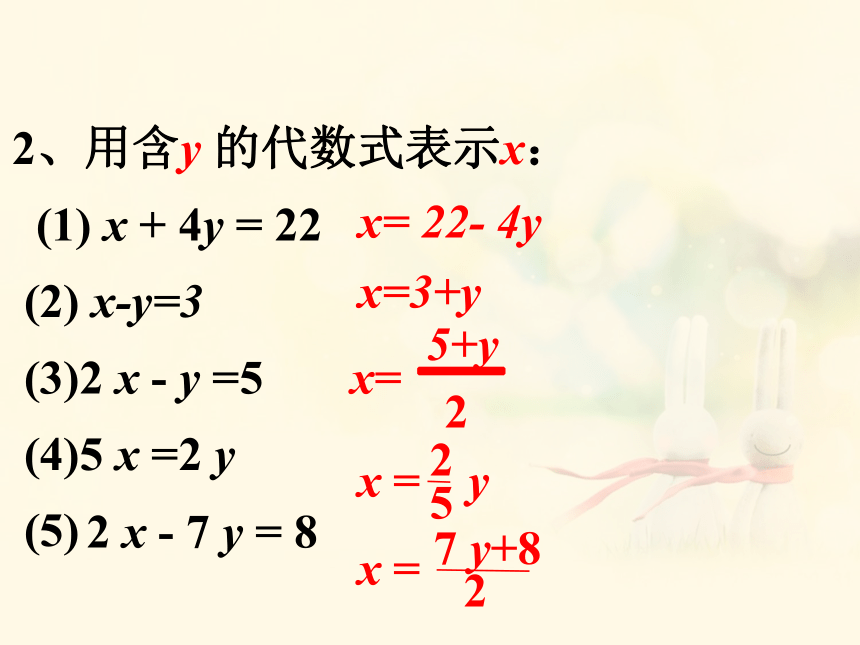


文档简介
七年级数学下册(人教版)
8.2.1 用代入消元法解二元一次方程组
学习目标 :
1、会用代入法解二元一次方程组。
2、感悟代入消元法所体现的化“未知 为已知”的转化思想,渗透 消元思想,掌握其解二元一次方程组的一般步骤。
3、经历探索代入消元法解方程组的过程,培养主动探索的精神。
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
名人语录
每日小题:
1、用含x的代数式表示y :
(1) 2x + y = 22
(2) x-y=3
(3)2 x - y =5
(4)5 x =2 y
(5)3x+2y=8
y= 22- 2x
y = x
2
5
y = 2 x -5
y=x-3
2
y=
-
8-3x
2、用含y 的代数式表示x:
(1) x + 4y = 22
(2) x-y=3
(3)2 x - y =5
(4)5 x =2 y
(5)
2 x - 7 y = 8
x= 22- 4y
x=3+y
x =
2
7 y+8
x=
2
-
5+y
x = y
5
2
我国明朝有一位著名数学家叫程大位,他的书中有一道名题,说的是:“100个和尚分100个馒头,大和尚每人吃三个,小和尚3人吃一个,问大、小和尚各多少?”
讲授新课
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一未知数.
这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
请同学们读一读:
例1 解方程组
①
②
x –y = 3
3x -8 y = 14
解1:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
9+3 y– 8 y = 14
– 5 y = 5
y = – 1
x=2
y = -1
∴这个方程组的解是
讲
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法
归 纳:
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴这个方程组的解是
x=5
y=2
由② 得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
练
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
由② 得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y = -10
y =2
把y=2代入③ ,得 x=5
议一议:用代入法解二元一次方程组的一般步骤
3、把这个未知数的值代入变形后的式子,求得另一个未知数的值;
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
4、写出方程组的解。
变
代
求
写
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
用代入法解下面方程组
限时比赛 看谁最快
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=3
y=0
你解对了吗?
1、用代入消元法解下列方程组
代
写
求
方程组
思想
转化
思想
消元
思想
二元 —— 一元
消
元
变
基本思路
数学思想
一般步骤
课堂小结
课本97页习题8.2
正式作业:第 1、2题
家庭作业:配套练习二
作 业
8.2.1 用代入消元法解二元一次方程组
学习目标 :
1、会用代入法解二元一次方程组。
2、感悟代入消元法所体现的化“未知 为已知”的转化思想,渗透 消元思想,掌握其解二元一次方程组的一般步骤。
3、经历探索代入消元法解方程组的过程,培养主动探索的精神。
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
名人语录
每日小题:
1、用含x的代数式表示y :
(1) 2x + y = 22
(2) x-y=3
(3)2 x - y =5
(4)5 x =2 y
(5)3x+2y=8
y= 22- 2x
y = x
2
5
y = 2 x -5
y=x-3
2
y=
-
8-3x
2、用含y 的代数式表示x:
(1) x + 4y = 22
(2) x-y=3
(3)2 x - y =5
(4)5 x =2 y
(5)
2 x - 7 y = 8
x= 22- 4y
x=3+y
x =
2
7 y+8
x=
2
-
5+y
x = y
5
2
我国明朝有一位著名数学家叫程大位,他的书中有一道名题,说的是:“100个和尚分100个馒头,大和尚每人吃三个,小和尚3人吃一个,问大、小和尚各多少?”
讲授新课
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一未知数.
这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
请同学们读一读:
例1 解方程组
①
②
x –y = 3
3x -8 y = 14
解1:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
9+3 y– 8 y = 14
– 5 y = 5
y = – 1
x=2
y = -1
∴这个方程组的解是
讲
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法
归 纳:
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴这个方程组的解是
x=5
y=2
由② 得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
练
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
由② 得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y = -10
y =2
把y=2代入③ ,得 x=5
议一议:用代入法解二元一次方程组的一般步骤
3、把这个未知数的值代入变形后的式子,求得另一个未知数的值;
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
4、写出方程组的解。
变
代
求
写
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
用代入法解下面方程组
限时比赛 看谁最快
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=3
y=0
你解对了吗?
1、用代入消元法解下列方程组
代
写
求
方程组
思想
转化
思想
消元
思想
二元 —— 一元
消
元
变
基本思路
数学思想
一般步骤
课堂小结
课本97页习题8.2
正式作业:第 1、2题
家庭作业:配套练习二
作 业
