湘教版(2012)初中数学七年级上册4.2 .1线段 射线 直线 课件(共27张)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册4.2 .1线段 射线 直线 课件(共27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 07:59:50 | ||
图片预览







文档简介
4.2 线段、射线、
直线
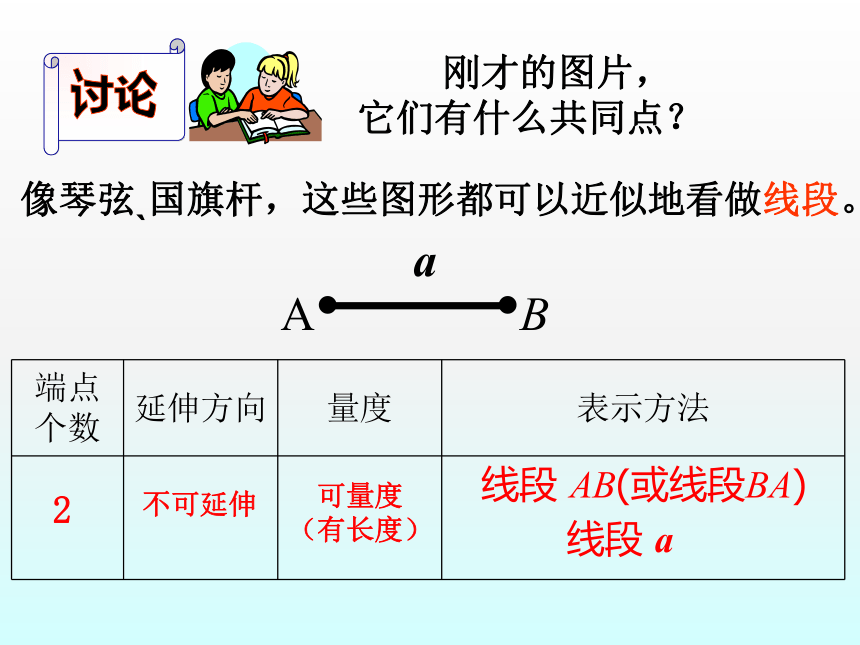
刚才的图片,它们有什么共同点?
像琴弦?国旗杆,这些图形都可以近似地看做线段。
A?
?B
a
讨论
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
线段 AB(或线段BA)
线段 a
2
不可延伸
可量度
(有长度)
除了以上这些可以
近似地看作线段,你还
能举出生活中的例子吗?
手电筒射出的光有什么特点?
可以近似地看作什么?
将线段向一个方向无限延长就得到了射线。
O
P
你知道吗?
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
1
向一方无限延伸
不可量度
(无长度)
①射线OP
O
P
②射线PO
①
②
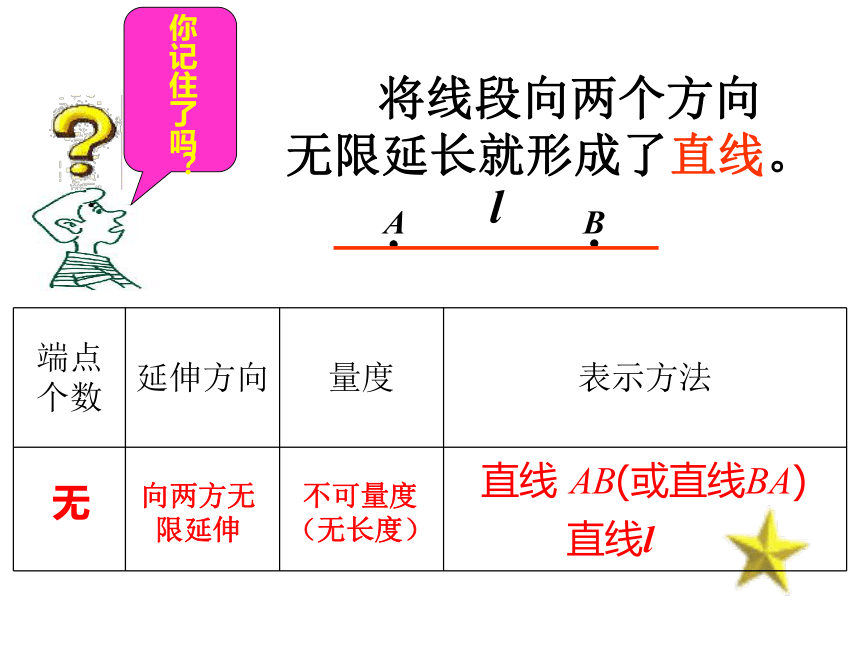
直线有什么特点?
将线段向两个方向无限延长就形成了直线。
A
B
l
你记住了吗?
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
无
向两方无限延伸
不可量度
(无长度)
直线 AB(或直线BA)
直线l
名称
线段
射线
直线
概念/定义
图形
端点
长度
表示方法
直线、射线、线段的区别:
连结两个端点之间的笔直的线
将线段向一个方向无限延长就得到了射线
将线段向两个方向无限延长就形成了直线
有两个端点
①线段 AB(BA)
②线段a
射线OP
①直线AB(BA)
②直线l
填一填
有
无
无
有一个端点
无端点
线段: ①用两个端点的字母来表示,无先后顺序.
②用一个小写字母表示.
射线: ① 用端点及射线上一点来表示,表示端 点 的字母要写在前面.
②用一个小写字母表示.
直线: ①?? 用直线上两个点来表示,无先后顺序.
②?? 用一个小写字母来表示.
归纳
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
P
记作:射线OP ( )
√
A
B
记作:线段BA ( )
√
请你来判断
5
画一条两厘米的直线。 ( )
×
O
1、用字母表示下面图形,图①记作________ ;图②记作 或 ;图③记作 ;
图④记作 或 。
① ② ③ ④
P
M N
O A
a
C D
m
点P
线段MN
线段a
射线OA
直线m
直线CD(DC)
考考你
已知线段AB,你能由线段AB得到射线AB和直线AB吗?
A
B
线段AB
直线AB
射线AB
① 线段向一端无限延长形成射线,向两端无限延长形成直 线;
② 射线向一端无限延长也能形成直线。
线段、射线、直线的联系
刚才我们了解了线段、射线、直线的特点,接下来 :
怎样画出线段、射线、直线?
如图,已知三点A、B、C
(1)画线段AB
(2)画射线AC
(3)画直线BC
A
B
C
? 画一画?
思考:
(1)点A与直线BC是怎样的位置关系?
(2)点B与直线BC呢?
现有一点O和一条直线a,你能画出他们的位置关系吗?
探究活动一
点与直线的位置关系
图形
几何语言
O
a
O
点O在直线a 上(直线a经过点O)
点O在直线a外(直线a不经过点O)
动手试一试
a
如图下列说法错误的是( )
A、点A在直线m上
B、点A在直线 l 上
C、点B在直线 l 上
D、直线m不经过B点
B
A
l
m
C
如图,尝试描述直线a直线b的位置关系
a
O
b
当两条不同的直线有一个公共点时,
我们就称这两条直线相交,这个公
共点叫做它们的交点
几何语言:
直线 a 和 b 相交于点O
交点
探究活动二
如图,点M在直线 上,
在直线 外;点O既在直线 上,也在直线 上;直线AB与直线CD相交于点
C
D
A
B
CD
AB
AB
CD
O
O
M
探究活动三
要在墙上固定一个衣架,并使它不能转动至少需要几个钉子?
·A
·A
·B
(1)过一点A可以画几条直线?
(2)过两点A、B可以画几条直线?
(1)
(2)
(无数条)
(一条)
试一试
直线的基本性质:
A
B
或简述为:
经过两点有一条直线,并且只有一条直线。
存在性
唯一性
两点确定一条直线
生活中的哪些实例, 应用了“两点确定一条直线” ?
议一议
两点确定一条直线的应用:
1、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
2、建筑工人在砌墙时,这样拉出的参照线就是直的(如图所示):
3、木工师傅用墨盒弹出的墨线也是直的:
谈谈本节课你有哪些收获?
3.知道了直线的基本性质:
两点确定一条直线。
2.掌握了直线、射线、线段的表示方法
1.理解了直线、射线、线段的特征及表示方法;
归纳 小结
课本第122页:
A组第1、2题
作业
直线
刚才的图片,它们有什么共同点?
像琴弦?国旗杆,这些图形都可以近似地看做线段。
A?
?B
a
讨论
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
线段 AB(或线段BA)
线段 a
2
不可延伸
可量度
(有长度)
除了以上这些可以
近似地看作线段,你还
能举出生活中的例子吗?
手电筒射出的光有什么特点?
可以近似地看作什么?
将线段向一个方向无限延长就得到了射线。
O
P
你知道吗?
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
1
向一方无限延伸
不可量度
(无长度)
①射线OP
O
P
②射线PO
①
②
直线有什么特点?
将线段向两个方向无限延长就形成了直线。
A
B
l
你记住了吗?
{5940675A-B579-460E-94D1-54222C63F5DA}端点个数
延伸方向
量度
表示方法
无
向两方无限延伸
不可量度
(无长度)
直线 AB(或直线BA)
直线l
名称
线段
射线
直线
概念/定义
图形
端点
长度
表示方法
直线、射线、线段的区别:
连结两个端点之间的笔直的线
将线段向一个方向无限延长就得到了射线
将线段向两个方向无限延长就形成了直线
有两个端点
①线段 AB(BA)
②线段a
射线OP
①直线AB(BA)
②直线l
填一填
有
无
无
有一个端点
无端点
线段: ①用两个端点的字母来表示,无先后顺序.
②用一个小写字母表示.
射线: ① 用端点及射线上一点来表示,表示端 点 的字母要写在前面.
②用一个小写字母表示.
直线: ①?? 用直线上两个点来表示,无先后顺序.
②?? 用一个小写字母来表示.
归纳
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
P
记作:射线OP ( )
√
A
B
记作:线段BA ( )
√
请你来判断
5
画一条两厘米的直线。 ( )
×
O
1、用字母表示下面图形,图①记作________ ;图②记作 或 ;图③记作 ;
图④记作 或 。
① ② ③ ④
P
M N
O A
a
C D
m
点P
线段MN
线段a
射线OA
直线m
直线CD(DC)
考考你
已知线段AB,你能由线段AB得到射线AB和直线AB吗?
A
B
线段AB
直线AB
射线AB
① 线段向一端无限延长形成射线,向两端无限延长形成直 线;
② 射线向一端无限延长也能形成直线。
线段、射线、直线的联系
刚才我们了解了线段、射线、直线的特点,接下来 :
怎样画出线段、射线、直线?
如图,已知三点A、B、C
(1)画线段AB
(2)画射线AC
(3)画直线BC
A
B
C
? 画一画?
思考:
(1)点A与直线BC是怎样的位置关系?
(2)点B与直线BC呢?
现有一点O和一条直线a,你能画出他们的位置关系吗?
探究活动一
点与直线的位置关系
图形
几何语言
O
a
O
点O在直线a 上(直线a经过点O)
点O在直线a外(直线a不经过点O)
动手试一试
a
如图下列说法错误的是( )
A、点A在直线m上
B、点A在直线 l 上
C、点B在直线 l 上
D、直线m不经过B点
B
A
l
m
C
如图,尝试描述直线a直线b的位置关系
a
O
b
当两条不同的直线有一个公共点时,
我们就称这两条直线相交,这个公
共点叫做它们的交点
几何语言:
直线 a 和 b 相交于点O
交点
探究活动二
如图,点M在直线 上,
在直线 外;点O既在直线 上,也在直线 上;直线AB与直线CD相交于点
C
D
A
B
CD
AB
AB
CD
O
O
M
探究活动三
要在墙上固定一个衣架,并使它不能转动至少需要几个钉子?
·A
·A
·B
(1)过一点A可以画几条直线?
(2)过两点A、B可以画几条直线?
(1)
(2)
(无数条)
(一条)
试一试
直线的基本性质:
A
B
或简述为:
经过两点有一条直线,并且只有一条直线。
存在性
唯一性
两点确定一条直线
生活中的哪些实例, 应用了“两点确定一条直线” ?
议一议
两点确定一条直线的应用:
1、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
2、建筑工人在砌墙时,这样拉出的参照线就是直的(如图所示):
3、木工师傅用墨盒弹出的墨线也是直的:
谈谈本节课你有哪些收获?
3.知道了直线的基本性质:
两点确定一条直线。
2.掌握了直线、射线、线段的表示方法
1.理解了直线、射线、线段的特征及表示方法;
归纳 小结
课本第122页:
A组第1、2题
作业
同课章节目录
