湘教版(2012)初中数学七年级上册4.2.1 线段 射线 直线 课件(共26张)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册4.2.1 线段 射线 直线 课件(共26张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
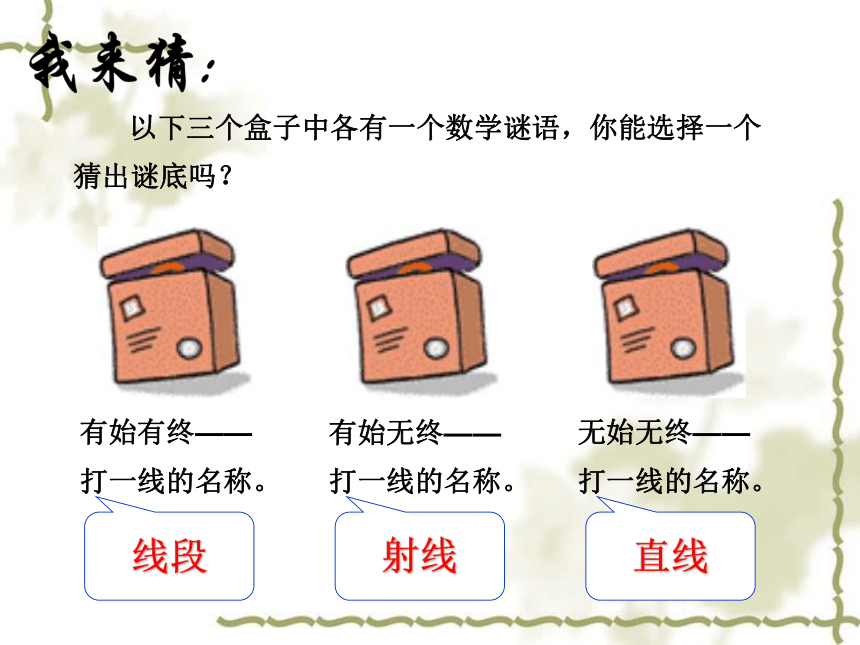
以下三个盒子中各有一个数学谜语,你能选择一个
猜出谜底吗?
有始有终——
打一线的名称。
有始无终——
打一线的名称。
无始无终——
打一线的名称。
线段
射线
直线
4.2.1 线段、射线、直线
生活中有哪些物体可以近似地看成线段、射线、直线?
笔直的马路给我们直线的形象
手电筒的光柱近似射线
旗杆看成线段
探究活动一:
认识线段、射线、直线
认识线段
问题1、谁能上黑板画一条线段?
问题2、要想知道这条线段有多长,我们该怎么办?
谁来量一量?
问题4、自己动手画一条4cm长的线段
问题5、线段的表示方法
(两个端点)
问题3、线段有哪些特征?
认识射线
问题1、如果将线段的一个端点去掉,使它能向一个方向无限延长,这样得到的是什么图形?
问题2、生活中哪些现象类似于射线?射线有什么特征?
问题3、请你从A点出发画一条射线。
问题4、射线的表示方法
还能画吗?能画多少条?
认识直线
问题1、如果将线段的两个端点都去掉,使它向两个方向无限延长,这样得到的是什么图形?
问题2、直线有什么特征?
问题3、直线的表示方法
类型
图形
表示 端点数
延伸情况
可否度量
区
别
直线
射线
线段
联
系
0个
1个
2个
不可度量
不可度量
可度量
向两个方向
无限延伸
向一个方向
无限延伸
1、线段向一端无限延伸形成射线,向两端无限延伸形成直
线;射线向一端无限延伸形成直线。
2、线段是射线的一部分,射线、线段都是直线的一部分。
不向任何
一方延伸
O
A
A
B
m
a
A
B
直线、射线、线段的区别和联系:
线段 AB(线段BA)
直线AB(直线BA)
线段 m
射线 OA
直线 a
表示方法:两大一小
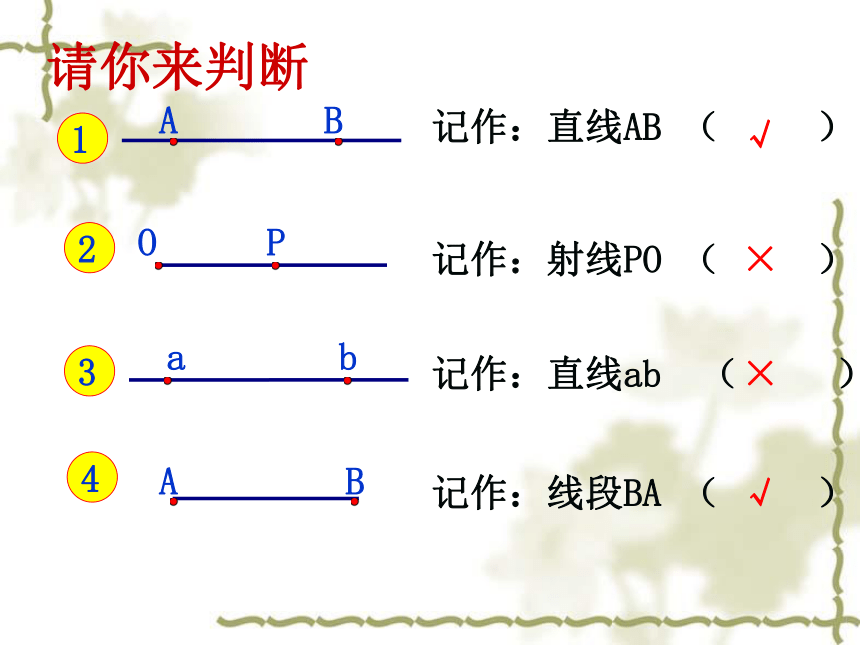
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
请你来判断
判断两条射线是否为同一条射线,应注意:
一看两条射线的 端点是否相同;
二看两条射线的 方向是否相同;
若两者都相同,则为同一条射线。
若有一方面不满足,则不是同一条射线。
如图:判断下面两条射线是否是同一射线:
A
B
C
(1)射线AB和射线AC ( )
(2)射线BA和射线BC ( )
(3)射线AC和射线BC ( )
√
×
×
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
针对训练
√
√
√
×
×
×
现有一点P和一条直线a,你能画出他们的位置关系吗?
探究活动二
图形
几何语言
P
a
P
点P在直线a 上(直线a经过点P)
点P在直线a外(直线a不经过点P)
动手试一试
a
点与直线的位置关系
a
b
O
当两条不同的直线有
一个公共点时,我们
就称这两条直线相交,
这个公共点叫做它们
的交点。
直线 a 和 b 相交于点O
交点
探究活动三
同一平面内直线与直线的位置关系
a
b
a(b)
当两条不同的直线
没有公共点时,我
们就称这两条直线
平行。
当两条不同的直线
有无数个公共点时
,我们就称这两条
直线重合
直线 a ∥ b
直线 a 和 b 重合
如图下列说法错误的是( )
A、点A在直线m上
B、点A在直线 l 上
C、点B在直线 l 上
D、直线m不经过B点
B
A
l
m
答案:C
针对训练
⑴ 过一点O 可以画几条直线?
⑵过两点A、B 可以画几条直线?
O
A
B
探究活动四:
基本事实
要在墙上固定一个衣架,并使它不能转动至少需要几个钉子?
这告诉我们一个什么道理?
想一想:
基本事实:
A
B
或简述为:
经过两点有一条直线,并且只有一条直线。
存在性
唯一性
两点确定一条直线。
生活中的哪些实例, 是用“两点确定一条直线” 来说明的?
针对训练
木匠师傅据木料时,一般先在木板上画两个点,然后过这两点弹出一条墨线,这是为什么?
植树时,要把一排树植整齐,要怎么办?
只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
1、下列说法正确的是( )
A、三点确定一条直线
B、延长直线AB到C
C、直线A与直线B相交于点M。
D、过一点可以作无数条直线
答案:D
巩固提高
一星题
2、如图所示的直线、射线、线段能相交的是( )
A
B
B
A
A
A
C
B
B
C
D
C
C
D
D
D
答案:C
(A)
(B)
(C)
(D)
二星题
巩固提高
A
B
D
C
1、说出下图中的直线、射线、线段。
2、在下面图中,过任意两点共能画几条直线?
巩固提高
三星题
二条直线相交有_ 个交点,三条直线相交最多有_ 个交点,四条直线相交最多有_ 个交点,n条直线相交最多有_ 个交点,最少有几个交点呢?
巩固提高
四星题
回顾一下,我想说…
? 直线、射线、线段的联系与区别.
? 直线 、射线 、线段的表示方法.
? 基本事实:两点确定一条直线.
课堂小结
? 点与直线的关系
? 直线与直线的关系
1.必做题:
课本134页习题3第4题.
2.挑战题:
⑴已知平面内的四个点A、B、C、D,过其中任意两个点可以作一条直线,则可以画出几条直线?若平面内有n个点呢?
⑵一条直线上有三个点,它们能组成多少条线段?四个点呢?试想有n个点,则能组成多少条线段?
⑶平面内有n条直线,最多能将平面分成多少个部分?
课后作业
感谢聆听
请各位老师批评指正!
猜出谜底吗?
有始有终——
打一线的名称。
有始无终——
打一线的名称。
无始无终——
打一线的名称。
线段
射线
直线
4.2.1 线段、射线、直线
生活中有哪些物体可以近似地看成线段、射线、直线?
笔直的马路给我们直线的形象
手电筒的光柱近似射线
旗杆看成线段
探究活动一:
认识线段、射线、直线
认识线段
问题1、谁能上黑板画一条线段?
问题2、要想知道这条线段有多长,我们该怎么办?
谁来量一量?
问题4、自己动手画一条4cm长的线段
问题5、线段的表示方法
(两个端点)
问题3、线段有哪些特征?
认识射线
问题1、如果将线段的一个端点去掉,使它能向一个方向无限延长,这样得到的是什么图形?
问题2、生活中哪些现象类似于射线?射线有什么特征?
问题3、请你从A点出发画一条射线。
问题4、射线的表示方法
还能画吗?能画多少条?
认识直线
问题1、如果将线段的两个端点都去掉,使它向两个方向无限延长,这样得到的是什么图形?
问题2、直线有什么特征?
问题3、直线的表示方法
类型
图形
表示 端点数
延伸情况
可否度量
区
别
直线
射线
线段
联
系
0个
1个
2个
不可度量
不可度量
可度量
向两个方向
无限延伸
向一个方向
无限延伸
1、线段向一端无限延伸形成射线,向两端无限延伸形成直
线;射线向一端无限延伸形成直线。
2、线段是射线的一部分,射线、线段都是直线的一部分。
不向任何
一方延伸
O
A
A
B
m
a
A
B
直线、射线、线段的区别和联系:
线段 AB(线段BA)
直线AB(直线BA)
线段 m
射线 OA
直线 a
表示方法:两大一小
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
请你来判断
判断两条射线是否为同一条射线,应注意:
一看两条射线的 端点是否相同;
二看两条射线的 方向是否相同;
若两者都相同,则为同一条射线。
若有一方面不满足,则不是同一条射线。
如图:判断下面两条射线是否是同一射线:
A
B
C
(1)射线AB和射线AC ( )
(2)射线BA和射线BC ( )
(3)射线AC和射线BC ( )
√
×
×
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
针对训练
√
√
√
×
×
×
现有一点P和一条直线a,你能画出他们的位置关系吗?
探究活动二
图形
几何语言
P
a
P
点P在直线a 上(直线a经过点P)
点P在直线a外(直线a不经过点P)
动手试一试
a
点与直线的位置关系
a
b
O
当两条不同的直线有
一个公共点时,我们
就称这两条直线相交,
这个公共点叫做它们
的交点。
直线 a 和 b 相交于点O
交点
探究活动三
同一平面内直线与直线的位置关系
a
b
a(b)
当两条不同的直线
没有公共点时,我
们就称这两条直线
平行。
当两条不同的直线
有无数个公共点时
,我们就称这两条
直线重合
直线 a ∥ b
直线 a 和 b 重合
如图下列说法错误的是( )
A、点A在直线m上
B、点A在直线 l 上
C、点B在直线 l 上
D、直线m不经过B点
B
A
l
m
答案:C
针对训练
⑴ 过一点O 可以画几条直线?
⑵过两点A、B 可以画几条直线?
O
A
B
探究活动四:
基本事实
要在墙上固定一个衣架,并使它不能转动至少需要几个钉子?
这告诉我们一个什么道理?
想一想:
基本事实:
A
B
或简述为:
经过两点有一条直线,并且只有一条直线。
存在性
唯一性
两点确定一条直线。
生活中的哪些实例, 是用“两点确定一条直线” 来说明的?
针对训练
木匠师傅据木料时,一般先在木板上画两个点,然后过这两点弹出一条墨线,这是为什么?
植树时,要把一排树植整齐,要怎么办?
只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
1、下列说法正确的是( )
A、三点确定一条直线
B、延长直线AB到C
C、直线A与直线B相交于点M。
D、过一点可以作无数条直线
答案:D
巩固提高
一星题
2、如图所示的直线、射线、线段能相交的是( )
A
B
B
A
A
A
C
B
B
C
D
C
C
D
D
D
答案:C
(A)
(B)
(C)
(D)
二星题
巩固提高
A
B
D
C
1、说出下图中的直线、射线、线段。
2、在下面图中,过任意两点共能画几条直线?
巩固提高
三星题
二条直线相交有_ 个交点,三条直线相交最多有_ 个交点,四条直线相交最多有_ 个交点,n条直线相交最多有_ 个交点,最少有几个交点呢?
巩固提高
四星题
回顾一下,我想说…
? 直线、射线、线段的联系与区别.
? 直线 、射线 、线段的表示方法.
? 基本事实:两点确定一条直线.
课堂小结
? 点与直线的关系
? 直线与直线的关系
1.必做题:
课本134页习题3第4题.
2.挑战题:
⑴已知平面内的四个点A、B、C、D,过其中任意两个点可以作一条直线,则可以画出几条直线?若平面内有n个点呢?
⑵一条直线上有三个点,它们能组成多少条线段?四个点呢?试想有n个点,则能组成多少条线段?
⑶平面内有n条直线,最多能将平面分成多少个部分?
课后作业
感谢聆听
请各位老师批评指正!
同课章节目录
