湘教版七年级上册第四章图形的认识复习与小结课件(共29张)
文档属性
| 名称 | 湘教版七年级上册第四章图形的认识复习与小结课件(共29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 680.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
图形的认识
小结与复习
[ 教学课件]
课程导入
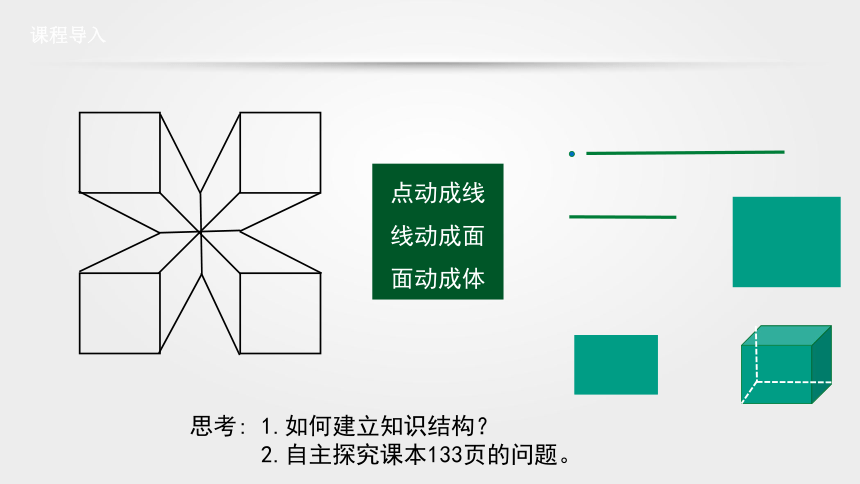
点动成线
线动成面
面动成体
思考: 1.如何建立知识结构?
2.自主探究课本133页的问题。
课程导入
1.直线、射线、线段有什么区别与联系?怎样比较线段的长短 ?
直线没有端点;射线只有一个端点;线段有两个端点。
度量比较法,叠合比较法。
2.什么样的图形是角?
具有公共端点的两条射线组成的图形叫做角
3.角的大小用什么单位表示 怎样比较两个角的大小
角度的单位就是度(°)、分(')、秒(")。度量比较法,叠合比较法。
4.同角成等角的余角有什么关系 同角成等角的补角有什么关系
同角(或等角)的余角相等,同角(或等角)的补角相等
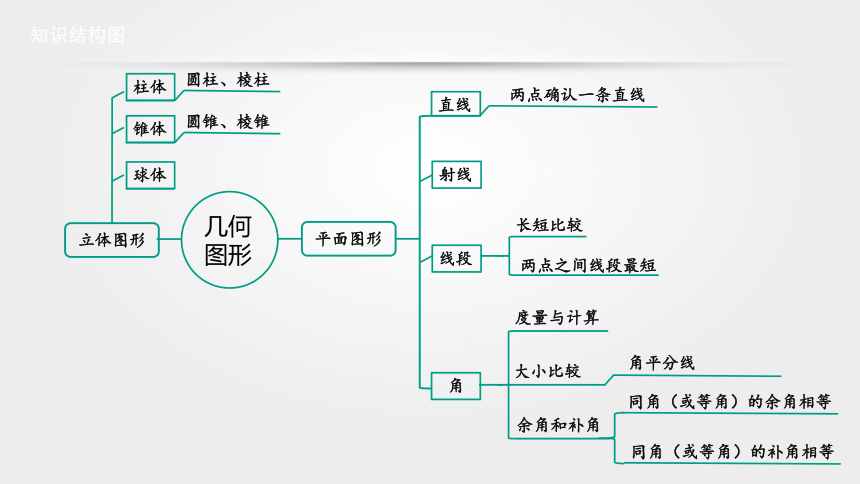
知识结构图
立体图形
平面图形
直线
射线
线段
角
两点确认一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角和补角
同角(或等角)的余角相等
同角(或等角)的补角相等
角平分线
几何
图形
柱体
圆柱、棱柱
锥体
圆锥、棱锥
球体
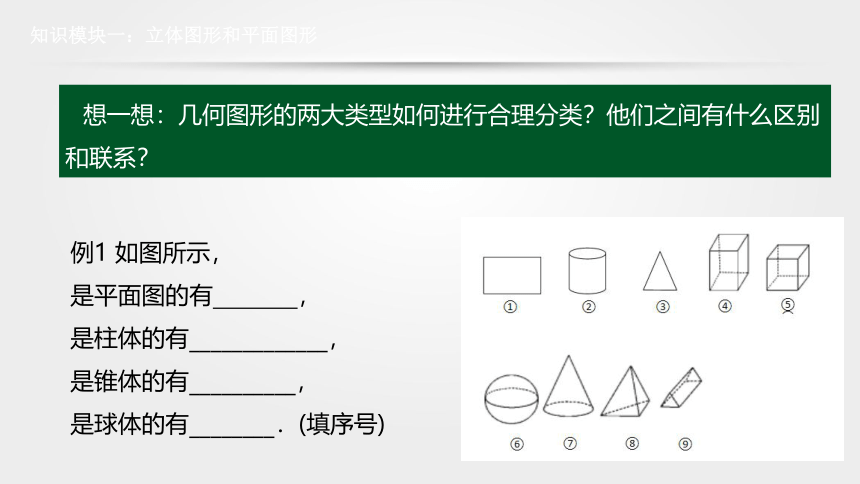
想一想:几何图形的两大类型如何进行合理分类?他们之间有什么区别和联系?
例1 如图所示,
是平面图的有 ,
是柱体的有_____________,
是锥体的有__________,
是球体的有________.(填序号)
知识模块一:立体图形和平面图形
知识模块一:立体图形和平面图形
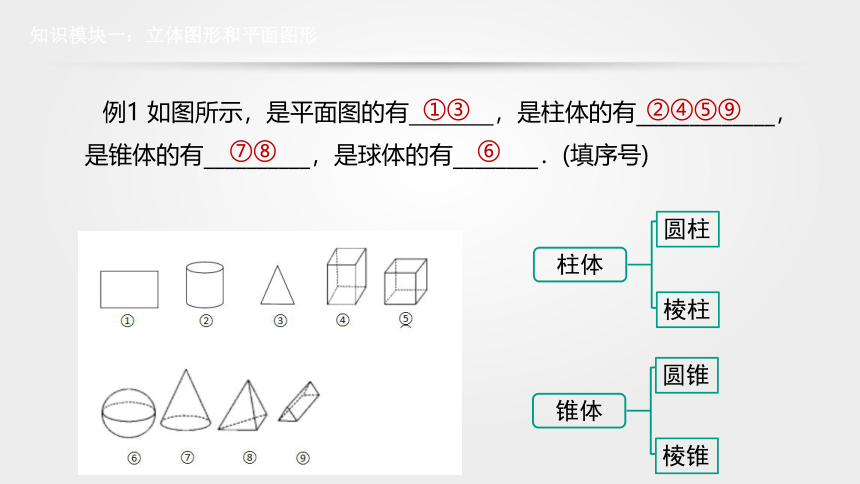
例1 如图所示,是平面图的有 ,是柱体的有_____________,是锥体的有__________,是球体的有________.(填序号)
①③
②④⑤⑨
⑦⑧
⑥
柱体
圆柱
棱柱
锥体
圆锥
棱锥
例2:如图是正方体的表面展开图,则与“前”相对的字是 ( )
A.认
B.真
C.复
D.习
B
知识模块一:立体图形和平面图形
知识模块一:立体图形和平面图形
想一想:立体图形和平面图形有什么联系,他们是否可以相互转换?
立体图形
展开或从不同方向看
面动成体
平面图形
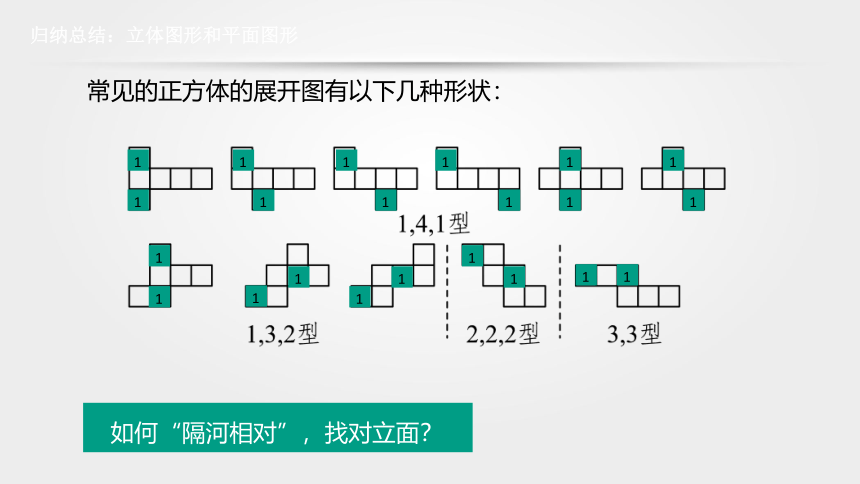
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
如何“隔河相对”,找对立面?
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
“隔河相对”,找对立面。
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
“隔河相对”,找对立面。
知识模块二:线段、直线、射线
图形 表示方法 端点数 延伸性 能否度量
线段
射线
直线
A
B
a
A
O
线段、直线、射线有什么区别呢?
知识模块二:线段、直线、射线
图形 表示方法 端点数 延伸性 能否度量
线段 2个 不能延伸 可度量
射线 1个 可向一个方向无限延伸 不可度量
直线 0个 可向两个方向无限延伸 不可度量
A
B
a
A
O
线段AB(或BA)
线段a
射线OA
直线AB (或BA)
直线
端点字母在前面
知识模块二:线段、直线、射线
知识回顾
1. 两直线相交只有 交点。2. 直线的基本性质:过两点 一条直线。(简称:两点确定一条直线) 3. 线段的基本性质:两点之间, 最短. 。4. 连接两点间的线段的 ,叫做这两点的距离。5. 线段中点:线段上的一点把一条线段分成 ,这一点叫这条线段的中点。
1个
有且只有
线段
端点
相等的两条线段
1.如图,C,D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
A.2cm B.3cm C.4cm D.6cm
例题3:线段的计算
B
想一想:如何判断一个点是线段的中点?如何从图形和数量上理解线段的和、差?
线段的计算是线段长度的的计算,可以像有理数一样进行和差运算
如下图,已知C为AB上一点,AB=12 cm,CB= AC,D,E分别为AC,AB的中点,求DE的长.
例题4:线段的计算
解:∵CB= AC,AB=12 cm,
∴AC+CB=AC+ AC=12 cm,
解得AC= cm.
∵D,E分别为AC,AB的中点,
∴AD= AC= cm,AE= AB=6 cm,
∴DE=AE-AD=6- = (cm).
12cm
1.方程思想在线段计算中的应用:
归纳总结:线段的计算
2.线段的中点的特征:
①中点在线段上;
②中点具有唯一性;
③中点把线段分成两条相等的线段.
若AC=BC,则点C不一定是线段AB的中点,因为点C不一定在线段AB上.
C
A
B
等腰三角形
知识模块三:角度的有关计算
知识回顾
1.角的定义:有公共端点的两条射线形成的图形。
2.角的分类:锐角、直角、钝角、平角、周角
3.角大小比较:叠合法、度量法
4.角的度量单位是度、分、秒,换算方法是: 1°=60',1'=60″,1'=( )°,1″=( )'
5.角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角。
6.余角:如果两角的和等于 90°(直角),就说这两个角互为余角,也就是说,其中一个角是另一个角的余角
互补角:如果两个角的和等于 180°(平角),就说这两个角互为补角,也就是说其中一个角是另一个角的补角。
7.角的性质:同角(或等角)的余角相等。同角(或等角)的补角相等。
例5:角度的有关计算
如果一个角的补角是它的余角的3倍,那么这个角的度数是( )
A.60° B.45° C.30° D.15°
想一想:如何从图形和数量上理解角的和、差关系?互余、互补是指角之间的位置关系还是数量关系?如何求已知角的余角或补角?
如果一个角的补角是它的余角的3倍,那么这个角的度数是( )
A.60° B.45° C.30° D.15°
解:设这个角为x°
那么它的补角是180°-x°,余角是90°-x°,
180°-x°=3(90°-x°)
所以180°-x°=270°-3x°,所以x°=45°.
B
例6:角度的有关计算
如图所示,已知∠AOB=120°,OC,OD分别为∠AOE,∠BOE的平分线.求∠COD的度数.
此题欲求∠COD的度数,可将∠COD转化为∠COE与∠DOE的和,然后再用角平分线的定义,将∠COE与∠DOE转化为∠AOE与∠BOE,而∠AOE与∠BOE之和恰好等于∠AOB,从而使问题得解.
例6:角度的有关计算
求∠COD的度数?
解:
因为OC,OD分别为∠AOE,∠BOE的平分线,
所以∠COE= ∠AOE,∠DOE= ∠BOE,
所以∠COD=∠COE+∠DOE= ∠AOE + ∠BOE
= (∠AOE+∠BOE)
= ∠AOB=×120°=60°.
故∠COD=60°.
例7:与线段、角有关的计数问题
(1)如下图,线段有________条;射线有________条;直线有________条.
(2)如下图,图中共有________个角.
6
8
1
6
例7:与线段、角有关的计数问题
探究四:一条直线上有多个不同的点时,如何计数出这些点组成多少条线段?由同一个点引出几条射线,如何计数出这些射线组成多少个小于平角的角?角的计数与线段的计数问题有什么区别吗?你能总结归纳出一般结论吗?
从左边开始,先将第一个点作为起点,与它右边的每一个点(作为终点)组成线段;再以第二个点为起点,与它右边的每一个点(作为终点)组成线段……依此类推,所得的线段条数之和为线段总条数.
图形计数
技巧
1
2
n(n-1)
2
例7:与线段、角有关的计数问题
直线上共有n个点,这n个点组成的线段有 条
平面内n条直线相交,最多共有 个交点
过平面内n个点(其中任意三点不在同一直线上)中的两个点可作 条直线.
从一点引出n条射线,可以组成 个角.
随堂测试
1.下列图形中是柱体的是( )
A. (2)(4) B. (1)(2) C.(5)(6) D.(3)(6)
练习2. 下列说法中,正确的有( )
(1)过两点有且只有一条线段; (2)连结两点的线段叫做两点的距离;
(3)两点之间,线段最短; (4)AB=BC,则点B是线段AC的中点;
(5) 射线比直线短.
A.1个 B.2个 C.3个 D.4个
练习3. 如图所示,OC平分∠AOD,OD平分∠BOC,
下列等式不成立的是( )
A. ∠AOC =∠BOD B. 2∠DOC =∠BOA
C. ∠AOC = ∠AOD D. ∠BOC =2∠BOD
随堂测试
练习4. 已知线段AB,延长AB至C,使BC=AB,D是AC的中点,如果DC=2cm,求AB的长.
练习5. 直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
随堂测试
汇报人:
感谢聆听
The teacher speaking lesson PPT
图形的认识
小结与复习
[ 教学课件]
课程导入
点动成线
线动成面
面动成体
思考: 1.如何建立知识结构?
2.自主探究课本133页的问题。
课程导入
1.直线、射线、线段有什么区别与联系?怎样比较线段的长短 ?
直线没有端点;射线只有一个端点;线段有两个端点。
度量比较法,叠合比较法。
2.什么样的图形是角?
具有公共端点的两条射线组成的图形叫做角
3.角的大小用什么单位表示 怎样比较两个角的大小
角度的单位就是度(°)、分(')、秒(")。度量比较法,叠合比较法。
4.同角成等角的余角有什么关系 同角成等角的补角有什么关系
同角(或等角)的余角相等,同角(或等角)的补角相等
知识结构图
立体图形
平面图形
直线
射线
线段
角
两点确认一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角和补角
同角(或等角)的余角相等
同角(或等角)的补角相等
角平分线
几何
图形
柱体
圆柱、棱柱
锥体
圆锥、棱锥
球体
想一想:几何图形的两大类型如何进行合理分类?他们之间有什么区别和联系?
例1 如图所示,
是平面图的有 ,
是柱体的有_____________,
是锥体的有__________,
是球体的有________.(填序号)
知识模块一:立体图形和平面图形
知识模块一:立体图形和平面图形
例1 如图所示,是平面图的有 ,是柱体的有_____________,是锥体的有__________,是球体的有________.(填序号)
①③
②④⑤⑨
⑦⑧
⑥
柱体
圆柱
棱柱
锥体
圆锥
棱锥
例2:如图是正方体的表面展开图,则与“前”相对的字是 ( )
A.认
B.真
C.复
D.习
B
知识模块一:立体图形和平面图形
知识模块一:立体图形和平面图形
想一想:立体图形和平面图形有什么联系,他们是否可以相互转换?
立体图形
展开或从不同方向看
面动成体
平面图形
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
如何“隔河相对”,找对立面?
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
“隔河相对”,找对立面。
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
归纳总结:立体图形和平面图形
常见的正方体的展开图有以下几种形状:
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
“隔河相对”,找对立面。
知识模块二:线段、直线、射线
图形 表示方法 端点数 延伸性 能否度量
线段
射线
直线
A
B
a
A
O
线段、直线、射线有什么区别呢?
知识模块二:线段、直线、射线
图形 表示方法 端点数 延伸性 能否度量
线段 2个 不能延伸 可度量
射线 1个 可向一个方向无限延伸 不可度量
直线 0个 可向两个方向无限延伸 不可度量
A
B
a
A
O
线段AB(或BA)
线段a
射线OA
直线AB (或BA)
直线
端点字母在前面
知识模块二:线段、直线、射线
知识回顾
1. 两直线相交只有 交点。2. 直线的基本性质:过两点 一条直线。(简称:两点确定一条直线) 3. 线段的基本性质:两点之间, 最短. 。4. 连接两点间的线段的 ,叫做这两点的距离。5. 线段中点:线段上的一点把一条线段分成 ,这一点叫这条线段的中点。
1个
有且只有
线段
端点
相等的两条线段
1.如图,C,D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
A.2cm B.3cm C.4cm D.6cm
例题3:线段的计算
B
想一想:如何判断一个点是线段的中点?如何从图形和数量上理解线段的和、差?
线段的计算是线段长度的的计算,可以像有理数一样进行和差运算
如下图,已知C为AB上一点,AB=12 cm,CB= AC,D,E分别为AC,AB的中点,求DE的长.
例题4:线段的计算
解:∵CB= AC,AB=12 cm,
∴AC+CB=AC+ AC=12 cm,
解得AC= cm.
∵D,E分别为AC,AB的中点,
∴AD= AC= cm,AE= AB=6 cm,
∴DE=AE-AD=6- = (cm).
12cm
1.方程思想在线段计算中的应用:
归纳总结:线段的计算
2.线段的中点的特征:
①中点在线段上;
②中点具有唯一性;
③中点把线段分成两条相等的线段.
若AC=BC,则点C不一定是线段AB的中点,因为点C不一定在线段AB上.
C
A
B
等腰三角形
知识模块三:角度的有关计算
知识回顾
1.角的定义:有公共端点的两条射线形成的图形。
2.角的分类:锐角、直角、钝角、平角、周角
3.角大小比较:叠合法、度量法
4.角的度量单位是度、分、秒,换算方法是: 1°=60',1'=60″,1'=( )°,1″=( )'
5.角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角。
6.余角:如果两角的和等于 90°(直角),就说这两个角互为余角,也就是说,其中一个角是另一个角的余角
互补角:如果两个角的和等于 180°(平角),就说这两个角互为补角,也就是说其中一个角是另一个角的补角。
7.角的性质:同角(或等角)的余角相等。同角(或等角)的补角相等。
例5:角度的有关计算
如果一个角的补角是它的余角的3倍,那么这个角的度数是( )
A.60° B.45° C.30° D.15°
想一想:如何从图形和数量上理解角的和、差关系?互余、互补是指角之间的位置关系还是数量关系?如何求已知角的余角或补角?
如果一个角的补角是它的余角的3倍,那么这个角的度数是( )
A.60° B.45° C.30° D.15°
解:设这个角为x°
那么它的补角是180°-x°,余角是90°-x°,
180°-x°=3(90°-x°)
所以180°-x°=270°-3x°,所以x°=45°.
B
例6:角度的有关计算
如图所示,已知∠AOB=120°,OC,OD分别为∠AOE,∠BOE的平分线.求∠COD的度数.
此题欲求∠COD的度数,可将∠COD转化为∠COE与∠DOE的和,然后再用角平分线的定义,将∠COE与∠DOE转化为∠AOE与∠BOE,而∠AOE与∠BOE之和恰好等于∠AOB,从而使问题得解.
例6:角度的有关计算
求∠COD的度数?
解:
因为OC,OD分别为∠AOE,∠BOE的平分线,
所以∠COE= ∠AOE,∠DOE= ∠BOE,
所以∠COD=∠COE+∠DOE= ∠AOE + ∠BOE
= (∠AOE+∠BOE)
= ∠AOB=×120°=60°.
故∠COD=60°.
例7:与线段、角有关的计数问题
(1)如下图,线段有________条;射线有________条;直线有________条.
(2)如下图,图中共有________个角.
6
8
1
6
例7:与线段、角有关的计数问题
探究四:一条直线上有多个不同的点时,如何计数出这些点组成多少条线段?由同一个点引出几条射线,如何计数出这些射线组成多少个小于平角的角?角的计数与线段的计数问题有什么区别吗?你能总结归纳出一般结论吗?
从左边开始,先将第一个点作为起点,与它右边的每一个点(作为终点)组成线段;再以第二个点为起点,与它右边的每一个点(作为终点)组成线段……依此类推,所得的线段条数之和为线段总条数.
图形计数
技巧
1
2
n(n-1)
2
例7:与线段、角有关的计数问题
直线上共有n个点,这n个点组成的线段有 条
平面内n条直线相交,最多共有 个交点
过平面内n个点(其中任意三点不在同一直线上)中的两个点可作 条直线.
从一点引出n条射线,可以组成 个角.
随堂测试
1.下列图形中是柱体的是( )
A. (2)(4) B. (1)(2) C.(5)(6) D.(3)(6)
练习2. 下列说法中,正确的有( )
(1)过两点有且只有一条线段; (2)连结两点的线段叫做两点的距离;
(3)两点之间,线段最短; (4)AB=BC,则点B是线段AC的中点;
(5) 射线比直线短.
A.1个 B.2个 C.3个 D.4个
练习3. 如图所示,OC平分∠AOD,OD平分∠BOC,
下列等式不成立的是( )
A. ∠AOC =∠BOD B. 2∠DOC =∠BOA
C. ∠AOC = ∠AOD D. ∠BOC =2∠BOD
随堂测试
练习4. 已知线段AB,延长AB至C,使BC=AB,D是AC的中点,如果DC=2cm,求AB的长.
练习5. 直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
随堂测试
汇报人:
感谢聆听
The teacher speaking lesson PPT
同课章节目录
