新湘教版年级九上册数学2.5一元二次方程的应用(1)课件(共24张PPT)
文档属性
| 名称 | 新湘教版年级九上册数学2.5一元二次方程的应用(1)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
湘教版·九年级上册
2.5 一元二次方程的应用
一元二次方程的应用(1)
1.某工厂一月份生产零件1000个,二月份生产零件
1200个,那么二月份比一月份增产______个,增长
率是多少 。
200
20%
2.某产品,原来每件的进价是500元,若每件售价625元,则每件利润是 每件利润率是 .
125元
25%
4.康佳生产彩电,第一个月生产了5000台,第二个月增产了50%,则:第二个月比第一个月增加了___________台,第二个月生产了_____________台;
5000×50%
5000(1+50%)
5.某农户第一年的粮食产量为100吨,平均每年的增长率为x,则第二年的产量为__________吨,第三年产量为________________吨,第四年的产量为___________吨,照这样计算,第n年的产量为 吨。
100(1+x)
100(1+x)(1+x)
100(1+x)2
100(1+x)3
100(1+x)n-1
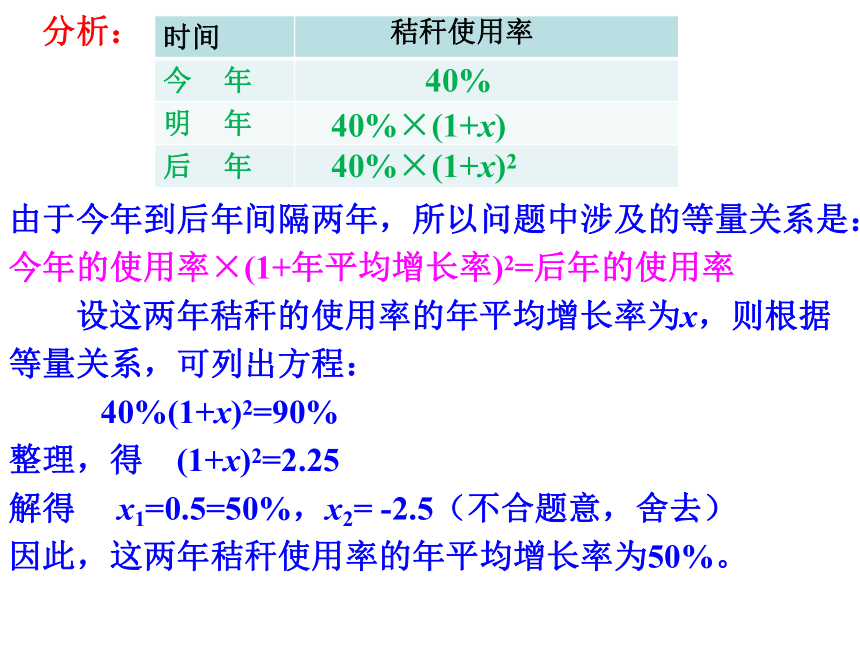
某省农作物秸秆资源巨大,但合理使用量十分有限,因此该省准备引进适用的新技术来提高秸秆的合理使用率,若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸秆使用率的年平均增长率(假定该省每年产生的秸秆总量不变)。
动脑筋
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率
设这两年秸秆的使用率的年平均增长率为x,则根据
等量关系,可列出方程:
40%(1+x)2=90%
整理,得 (1+x)2=2.25
解得 x1=0.5=50%,x2= -2.5(不合题意,舍去)
因此,这两年秸秆使用率的年平均增长率为50%。
分析:
时间
今 年
明 年
后 年
40%
40%×(1+x)
秸秆使用率
40%×(1+x)2
例1 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,求平均每次降价的百分率。
问题中涉及的等量关系是:
原价×(1-平均每次降价的百分率)2=现行售价
举
例
分析:
时 间
药品的价格
原 来
第一次
第二次
100元
100×(1-x)元
100×(1-x)2元
解:设平均每次降价的百分率为x,则根据等量
关系得:
100(1-x)2=81
整理,得 (1-x)2=0.81
解得 x1=0.1=10%,x2=1.9(不合题意,舍去)
答:平均每次降价的百分率为10%。
原价×(1-平均每次降价的百分率)2=现行售价
为什么x=1.9不合题意呢?
结论
增长率(或降低率)问题:
(1)原有量×(1+平均增长率)增长次数 = 现有量;
(2)原有量×(1-平均降低率)降低次数 = 现有量;
注意:
增长率(或降低率)问题一般用直接开平方法求解:
随堂练习
3
4
补充例题 某班有若干人,新年晚会上互相握手问候,若全班共握手820次,则这个班共有多少人?
解:设这个班共有x人,依题意可列方程:
答:这个班共有41人.
结论
循环问题:
注意:
单循环要除以2,双循环不要除以2.
练习:一个小组有若干人,新年互送贺卡,若全组共送贺卡72张,则这个小组共有多少人?
(握手,互送礼物,比赛等)
例2 某商店从厂家以每件21元的价格购进一批商品,若每件商品的售价为x元,则可卖出(350-10x)件,但物价局限定每件商品的售价不能超过进价的120%,若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
分析:本问题中涉及的等量关系是:
单件商品的利润×销售量=总利润。
解:根据等量关系得: (x-21)(350-10x)=400
整理,得 x2-56x+775=0
解得 x1=25,x2=31
又因为21×120%=25.2,即售价不能超过25.2元,
所以x=31不合题意,应当舍去,
故x=25,从而卖出350-10x=350-10×25=100(件)
答:该商店需要卖出100件商品,且每件商品的售价是25元。
( 售价 - 进价 )
补例 某商场礼品柜台春节期间购进大量贺年岁片,一种贺岁片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施.调查表明:当销售价每降价0.1元时,其销售量就将多售出100张.商场要想平均每天盈利达到120元,每张贺岁片应降价多少元?
本题涉及的等量关系为:
单件产品利润×销售量=总利润
结论
销售问题:
单件产品的利润×销售量=总利润
运用一元二次方程模型解决实际问题的步骤有哪些?
实际问题
建立一元二
次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
议一议
议一议
议一议
议一议
议一议
议一议
1.坐石中心学校图书馆的藏书在两年内从5万册增加到7.2万册,平均每年增长的百分率是多少?
练习
2.新东方服装专营店平均每天可销售该品牌服装20件,每件可盈利44元.若每件降价1元,则每天可多售出5件.若要平均每天盈利1600元,则应降价多少元?
1.娄底市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?
提高练习
解:设平均年增长率应为
,依题意,得
,
,
答:这两年中财政净收入的平均年增长率约为41.4%
2
3
4
谈谈今天的收获
一元二次方程的应用 ;
列方程解应用题的一般步骤;
具体问题中如何设未知数;
列方程解应用题应注意的问题;
如何寻找等量关系。
2.5 一元二次方程的应用
一元二次方程的应用(1)
1.某工厂一月份生产零件1000个,二月份生产零件
1200个,那么二月份比一月份增产______个,增长
率是多少 。
200
20%
2.某产品,原来每件的进价是500元,若每件售价625元,则每件利润是 每件利润率是 .
125元
25%
4.康佳生产彩电,第一个月生产了5000台,第二个月增产了50%,则:第二个月比第一个月增加了___________台,第二个月生产了_____________台;
5000×50%
5000(1+50%)
5.某农户第一年的粮食产量为100吨,平均每年的增长率为x,则第二年的产量为__________吨,第三年产量为________________吨,第四年的产量为___________吨,照这样计算,第n年的产量为 吨。
100(1+x)
100(1+x)(1+x)
100(1+x)2
100(1+x)3
100(1+x)n-1
某省农作物秸秆资源巨大,但合理使用量十分有限,因此该省准备引进适用的新技术来提高秸秆的合理使用率,若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸秆使用率的年平均增长率(假定该省每年产生的秸秆总量不变)。
动脑筋
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率
设这两年秸秆的使用率的年平均增长率为x,则根据
等量关系,可列出方程:
40%(1+x)2=90%
整理,得 (1+x)2=2.25
解得 x1=0.5=50%,x2= -2.5(不合题意,舍去)
因此,这两年秸秆使用率的年平均增长率为50%。
分析:
时间
今 年
明 年
后 年
40%
40%×(1+x)
秸秆使用率
40%×(1+x)2
例1 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,求平均每次降价的百分率。
问题中涉及的等量关系是:
原价×(1-平均每次降价的百分率)2=现行售价
举
例
分析:
时 间
药品的价格
原 来
第一次
第二次
100元
100×(1-x)元
100×(1-x)2元
解:设平均每次降价的百分率为x,则根据等量
关系得:
100(1-x)2=81
整理,得 (1-x)2=0.81
解得 x1=0.1=10%,x2=1.9(不合题意,舍去)
答:平均每次降价的百分率为10%。
原价×(1-平均每次降价的百分率)2=现行售价
为什么x=1.9不合题意呢?
结论
增长率(或降低率)问题:
(1)原有量×(1+平均增长率)增长次数 = 现有量;
(2)原有量×(1-平均降低率)降低次数 = 现有量;
注意:
增长率(或降低率)问题一般用直接开平方法求解:
随堂练习
3
4
补充例题 某班有若干人,新年晚会上互相握手问候,若全班共握手820次,则这个班共有多少人?
解:设这个班共有x人,依题意可列方程:
答:这个班共有41人.
结论
循环问题:
注意:
单循环要除以2,双循环不要除以2.
练习:一个小组有若干人,新年互送贺卡,若全组共送贺卡72张,则这个小组共有多少人?
(握手,互送礼物,比赛等)
例2 某商店从厂家以每件21元的价格购进一批商品,若每件商品的售价为x元,则可卖出(350-10x)件,但物价局限定每件商品的售价不能超过进价的120%,若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
分析:本问题中涉及的等量关系是:
单件商品的利润×销售量=总利润。
解:根据等量关系得: (x-21)(350-10x)=400
整理,得 x2-56x+775=0
解得 x1=25,x2=31
又因为21×120%=25.2,即售价不能超过25.2元,
所以x=31不合题意,应当舍去,
故x=25,从而卖出350-10x=350-10×25=100(件)
答:该商店需要卖出100件商品,且每件商品的售价是25元。
( 售价 - 进价 )
补例 某商场礼品柜台春节期间购进大量贺年岁片,一种贺岁片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施.调查表明:当销售价每降价0.1元时,其销售量就将多售出100张.商场要想平均每天盈利达到120元,每张贺岁片应降价多少元?
本题涉及的等量关系为:
单件产品利润×销售量=总利润
结论
销售问题:
单件产品的利润×销售量=总利润
运用一元二次方程模型解决实际问题的步骤有哪些?
实际问题
建立一元二
次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
议一议
议一议
议一议
议一议
议一议
议一议
1.坐石中心学校图书馆的藏书在两年内从5万册增加到7.2万册,平均每年增长的百分率是多少?
练习
2.新东方服装专营店平均每天可销售该品牌服装20件,每件可盈利44元.若每件降价1元,则每天可多售出5件.若要平均每天盈利1600元,则应降价多少元?
1.娄底市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?
提高练习
解:设平均年增长率应为
,依题意,得
,
,
答:这两年中财政净收入的平均年增长率约为41.4%
2
3
4
谈谈今天的收获
一元二次方程的应用 ;
列方程解应用题的一般步骤;
具体问题中如何设未知数;
列方程解应用题应注意的问题;
如何寻找等量关系。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
