必修5 第1章解三角综合测试题-2020-2021学年高二数学(理)上学期期末复习(人教B版)Word含解析
文档属性
| 名称 | 必修5 第1章解三角综合测试题-2020-2021学年高二数学(理)上学期期末复习(人教B版)Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




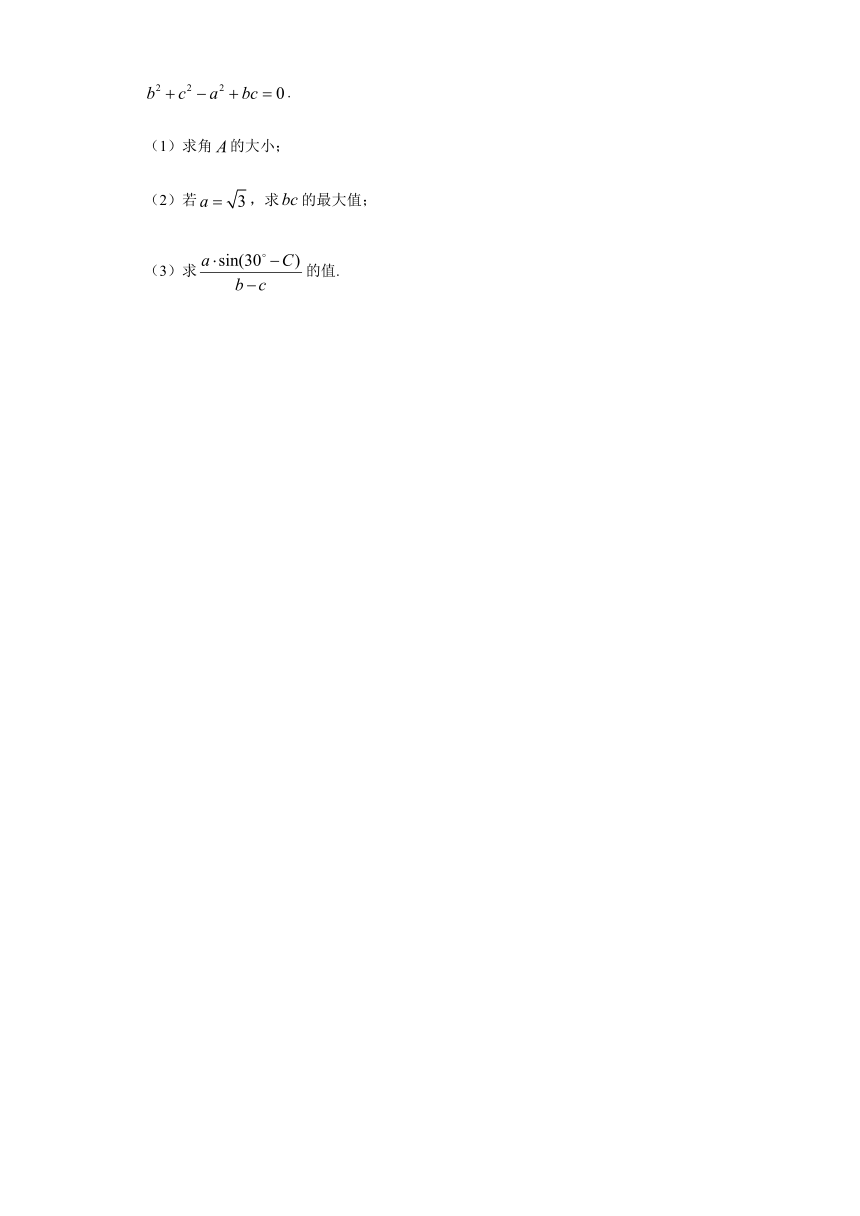
文档简介
人教B版必修5第一章解三角综合测试题
一、单选题
1.在中,、、分别为的内角、、的对边,、、,则( )
A.
B.
C.
D.
2.在中,已知,则( ).
A.2 B. C. D.
3.若点在点的北偏西,则点在点的( )
A.北偏西 B.北偏西
C.南偏东 D.东偏南
4.在中,角A,B,C所对的边分别为a,b,c,已知a,b,c成等比数列,且,则A等于( )
A. B. C. D.
5.已知中,,,,则其面积等于( )
A.或 B. C.或 D.
6.在中,,,,则( )
A. B. C. D.
7.在中,,,的面积为,则外接圆面积为( )
A. B. C. D.
8.在中,,,分别是角,,的对边,若,则( )
A. B. C. D.
9.设为的内心,延长线段交线段于点,若,则( )
A. B.
C. D.
10.在中,,若三角形有两解,则x的取值范围为( )
A. B. C. D.
11.中角A,B,C所对的边分别为a,b,c,若,则( )
A.1 B.-1 C. D.
12.在中,角,,所对的边分别为,,,已知,且,则周长的取值范围是( )
A. B. C. D.
二、填空题
13.在中,角所对的边为,若,则角的大小为__________.
14.在中,三个内角的对边分别为.若,,则____________.
15.已知的内角的对边分别为,若的面积为,则_____.
16.如图,在平面四边形中,,,,,则的最小值为_______.
三、解答题
17.
设的内角所对的边分别为.已知,,.
(Ⅰ)求的周长;
(Ⅱ)求的值.
18.已知中,角的对边分别为,且的面积,
(1)求的取值范围;
(2)求函数的最值.
19.在中,角,,所对的边分别为,,,,,.
(1)求的值;
(2)若为锐角三角形,求的面积.
20.如图,已知平面四边形中,为正三角形,,,记四边形的面积为.
(1)将表示为的函数;
(2)求的最大值及相应的值.
21.已知中,a,b,c分别为角A,B,C的对边,且
(1)求角C;
(2)若,求的最大值.
22.中,、、分别为的内角、、的对边,且.
(1)求角的大小;
(2)若,求的最大值;
(3)求的值.
参考答案
1.D
【分析】
根据题中条件,由正弦定理,得到,进而可得.
【详解】
由正弦定理得:,∴,
∵,∴,故角为锐角,
∴.
故选:D.
2.A
【分析】
根据正弦定理,得到,即可求解.
【详解】
由题意知,可得
根据正弦定理,可得,
所以.
故选:A.
3.C
【分析】
先作图,观察方向角即得结果.
【详解】
如图,
点在点的南偏东,
故选:C.
4.A
【分析】
由题意,结合余弦定理求出即可得到的值.
【详解】
解:、、成等比数列,所以,因为,所以,由余弦定理可知,因为
所以
故选:A
5.C
【分析】
利用余弦定理可构造方程求得,代入三角形面积公式可求得结果.
【详解】
在中,由余弦定理得:,
解得:或,
当时,;
当时,;
综上所述:的面积为或.
故选:C.
6.C
【分析】
先根据余弦定理求,再根据余弦定理求,最后根据同角三角函数关系求
【详解】
设,
,
.
故选:C.
7.C
【分析】
先由三角形面积公式求出,再由弦定理求出,则可由求出,即可得外接圆面积.
【详解】
在中,
,则,
根据余弦定理:
,
则,外接圆直径
,则,
外接圆面积.
故选:C
8.C
【分析】
根据条件由正弦定理可得,再根据余弦定理可得得出答案.
【详解】
由,得,可得
所以,则
又,所以
故选:C
9.B
【分析】
由三角形的面积有,从而得出答案.
【详解】
由为的内心,则为的角平分线,即
由
所以
故选:B
10.C
【分析】
由正弦定理分析.
【详解】
三角形有两解.由正弦定理得,即,解得.
故选:C.
【点睛】
易错点睛:在用正弦定理和余弦定理解三角形时,只有已知两边和一边对角时可能会出现两解的情形.如已知时,如果,则三角形有两解,其他都只会有一解或无解.在记不住条件时,可以先计算,只有,三角形才有解,当时再判断和的关系,如果,则有两解,否则只有一解.
11.B
【分析】
由已知和正弦定理得到,再根据得到,结合余弦定理可得答案.
【详解】
由及正弦定理得,
三角形中,
所以,
因为,所以,由余弦定理得,
故选:B.
【点睛】
本题考查了正弦定理、余弦定理解三角形问题,在解决有关三角形的问题时,正、余弦定理是一个很重要的工具,它们可单独或者联合解决一些问题.
12.B
【分析】
把已知式中2换成后用正弦定理化边为角,由三角函数恒等变换可得,然后由正弦定理把用角表示,得周长的表达式,求出角范围后可得周长的范围,
【详解】
因为,,所以,
所以,
所以,则,即.
由正弦定理可得,
则,,
故的周长.
因为解得,则,故的周长.
故选:B.
【点睛】
关键点点睛:本题主要考查正弦定理,解题关键是把已知等式中的2用边替换,这样可用正弦定理进行边角转化,化边为角,从而求得,然后可得角范围,同时再用正弦定理求出边(表示为的函数),从而可求得周长的范围.
13.
【分析】
由正弦定理化简已知等式可得,结合,可得,结合范围,可得,可得,即可得解的值.
【详解】
解:,
由正弦定理可得:,
,
,
,,
,
.
故答案为:.
14.
【分析】
利用同角三角函数关系求得的值,再利用正弦定理先求出.
【详解】
由题意知,所以为锐角,且,
又,,
,
在中,由正弦定理得,
即,所以,
故答案为:.
【点睛】
本题考查正弦定理在解三角形中的应用,涉及同角三角函数的关系,难度较易.
(1)已知三角形的两角与其中一角的对边,解三角形时只需要求得两角的正弦值,然后代入正弦定理即可得解;
(2)已知三角形的两角及第三边时,要先利用两角和的三角函数公式求得另一角的正弦值,然后再利用正弦定理求解.
15.
【分析】
利用三角形面积公式和余弦定理可求得,由同角三角函数关系可求得结果.
【详解】
,,,
又,,,.
故答案为:.
16.
【分析】
设,在中,利用正弦定理得,由余弦定理得,然后在中,由余弦定理得(其中),从而可求出的最小值
【详解】
设,在中,由正弦定理得,即
整理得.
由余弦定理得,
因为,所以.
在中,
由余弦定理得
(其中),
所以当时,.
故答案为:
【点睛】
关键点点睛:此题考查正弦定理和余弦定理的应用,解题的关键是在中,求出和,其中,再在中,利用余弦定理表示出,从而可求得结果,考查计算能力,属于中档题
17.(Ⅰ)的周长为5;.
(Ⅱ)
.
【解析】
分析:(I)利用余弦定理表示出的平方,把的值代入求出的值,从而求出三角形的周长;
(II)根据的值,利用同角三角函数间的基本关系求出的值,利用正弦定理即可求出的值,根据大边对大角,可得为锐角,利用同角三角函数间的基本关系求出 的值,然后利用两角差的余弦函数公式化简所求的式子,把各自的值代入即可求出值.
详解:(I)
的周长为
(II) 由正弦定理
,故为锐角.则
.
点睛:本题主要考查三角函数的基本公式和解斜三角形的基础知识,同时考查学生的基本运算能力,是一道基础题.
18.(1);(2)无最小值,时取得最大值为
【分析】
(1)由三角形面积公式结合题中条件可求出的范围,进而可求出结果;
(2)先化简,再根据(1)的结果,结合正弦函数的性质即可求出结果.
【详解】
解:(1)由三角形面积公式可得,又
则,
;
(2)由题意,
无最小值,时取得最大值为.
【点睛】
本题主要考查三角函数的性质,熟记正弦函数的性质即可,属于常考题型.
19.(1);(2).
【分析】
(1)根据正弦定理,由题中条件,求出外接圆的半径,进而可求出;
(2)先由(1)求出,根据余弦定理,求出的值,并检验,再由三角形面积公式,即可得出结果.
【详解】
(1)根据正弦定理,由可化为(其中为外接圆半径),
因为,,所以,
则;
(2)因为为锐角三角形,所,
由余弦定理可得:,即,
解得或,
当时,,此时为钝角,舍去.
所以,则.
20.(1);(2)当时,的最大值为.
【分析】
(1)先由余弦定理得,再由三角形面积公式可得函数关系.
(2)由(1)所得函数关系,整理后得正弦型函数关系,可得最值.
【详解】
解:(1),
∴中,,
∵为正三角形
∴
∴四边形的面积为
,其中
(2)由(1)得,当时,
即时,的最大值为.
【点睛】
本题为三角应用题,考查余弦定理及面积公式,属于基础题.
21.(1);(2)最大值为4.
【分析】
(1)利用正弦定理和三角函数的和差公式可得答案;
(2)由可求出,然后,然后可得答案.
【详解】
(1)∵,
∴,
∴,
∵,∴,
∴,∴.
(2)设的外接圆半径为R,∵,
∴,
∴
.
∵,∴,
当,即时,,即的最大值为4
22.(1);(2)1;(3).
【分析】
(1)根据,利用余弦定理求解.
(2)由,结合余弦定理得到,再利用基本不等式求解.
(3)由正弦定理,转化为,利用两角和与差的三角函数的三角函数求解.
【详解】
(1)∵中,,
∵,
∴由余弦定理得:,
∵,
∴;
(2)因为,由余弦定理得,
又∵(当且仅当时取等号),
∴,当且仅当时,取等号
所以取得最大值为;
(3)由正弦定理,得,
∴
,
∵
,
∴
【点睛】
方法点睛:在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息,一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到,解题中注意三角形内角和定理的应用及角的范围限制.
一、单选题
1.在中,、、分别为的内角、、的对边,、、,则( )
A.
B.
C.
D.
2.在中,已知,则( ).
A.2 B. C. D.
3.若点在点的北偏西,则点在点的( )
A.北偏西 B.北偏西
C.南偏东 D.东偏南
4.在中,角A,B,C所对的边分别为a,b,c,已知a,b,c成等比数列,且,则A等于( )
A. B. C. D.
5.已知中,,,,则其面积等于( )
A.或 B. C.或 D.
6.在中,,,,则( )
A. B. C. D.
7.在中,,,的面积为,则外接圆面积为( )
A. B. C. D.
8.在中,,,分别是角,,的对边,若,则( )
A. B. C. D.
9.设为的内心,延长线段交线段于点,若,则( )
A. B.
C. D.
10.在中,,若三角形有两解,则x的取值范围为( )
A. B. C. D.
11.中角A,B,C所对的边分别为a,b,c,若,则( )
A.1 B.-1 C. D.
12.在中,角,,所对的边分别为,,,已知,且,则周长的取值范围是( )
A. B. C. D.
二、填空题
13.在中,角所对的边为,若,则角的大小为__________.
14.在中,三个内角的对边分别为.若,,则____________.
15.已知的内角的对边分别为,若的面积为,则_____.
16.如图,在平面四边形中,,,,,则的最小值为_______.
三、解答题
17.
设的内角所对的边分别为.已知,,.
(Ⅰ)求的周长;
(Ⅱ)求的值.
18.已知中,角的对边分别为,且的面积,
(1)求的取值范围;
(2)求函数的最值.
19.在中,角,,所对的边分别为,,,,,.
(1)求的值;
(2)若为锐角三角形,求的面积.
20.如图,已知平面四边形中,为正三角形,,,记四边形的面积为.
(1)将表示为的函数;
(2)求的最大值及相应的值.
21.已知中,a,b,c分别为角A,B,C的对边,且
(1)求角C;
(2)若,求的最大值.
22.中,、、分别为的内角、、的对边,且.
(1)求角的大小;
(2)若,求的最大值;
(3)求的值.
参考答案
1.D
【分析】
根据题中条件,由正弦定理,得到,进而可得.
【详解】
由正弦定理得:,∴,
∵,∴,故角为锐角,
∴.
故选:D.
2.A
【分析】
根据正弦定理,得到,即可求解.
【详解】
由题意知,可得
根据正弦定理,可得,
所以.
故选:A.
3.C
【分析】
先作图,观察方向角即得结果.
【详解】
如图,
点在点的南偏东,
故选:C.
4.A
【分析】
由题意,结合余弦定理求出即可得到的值.
【详解】
解:、、成等比数列,所以,因为,所以,由余弦定理可知,因为
所以
故选:A
5.C
【分析】
利用余弦定理可构造方程求得,代入三角形面积公式可求得结果.
【详解】
在中,由余弦定理得:,
解得:或,
当时,;
当时,;
综上所述:的面积为或.
故选:C.
6.C
【分析】
先根据余弦定理求,再根据余弦定理求,最后根据同角三角函数关系求
【详解】
设,
,
.
故选:C.
7.C
【分析】
先由三角形面积公式求出,再由弦定理求出,则可由求出,即可得外接圆面积.
【详解】
在中,
,则,
根据余弦定理:
,
则,外接圆直径
,则,
外接圆面积.
故选:C
8.C
【分析】
根据条件由正弦定理可得,再根据余弦定理可得得出答案.
【详解】
由,得,可得
所以,则
又,所以
故选:C
9.B
【分析】
由三角形的面积有,从而得出答案.
【详解】
由为的内心,则为的角平分线,即
由
所以
故选:B
10.C
【分析】
由正弦定理分析.
【详解】
三角形有两解.由正弦定理得,即,解得.
故选:C.
【点睛】
易错点睛:在用正弦定理和余弦定理解三角形时,只有已知两边和一边对角时可能会出现两解的情形.如已知时,如果,则三角形有两解,其他都只会有一解或无解.在记不住条件时,可以先计算,只有,三角形才有解,当时再判断和的关系,如果,则有两解,否则只有一解.
11.B
【分析】
由已知和正弦定理得到,再根据得到,结合余弦定理可得答案.
【详解】
由及正弦定理得,
三角形中,
所以,
因为,所以,由余弦定理得,
故选:B.
【点睛】
本题考查了正弦定理、余弦定理解三角形问题,在解决有关三角形的问题时,正、余弦定理是一个很重要的工具,它们可单独或者联合解决一些问题.
12.B
【分析】
把已知式中2换成后用正弦定理化边为角,由三角函数恒等变换可得,然后由正弦定理把用角表示,得周长的表达式,求出角范围后可得周长的范围,
【详解】
因为,,所以,
所以,
所以,则,即.
由正弦定理可得,
则,,
故的周长.
因为解得,则,故的周长.
故选:B.
【点睛】
关键点点睛:本题主要考查正弦定理,解题关键是把已知等式中的2用边替换,这样可用正弦定理进行边角转化,化边为角,从而求得,然后可得角范围,同时再用正弦定理求出边(表示为的函数),从而可求得周长的范围.
13.
【分析】
由正弦定理化简已知等式可得,结合,可得,结合范围,可得,可得,即可得解的值.
【详解】
解:,
由正弦定理可得:,
,
,
,,
,
.
故答案为:.
14.
【分析】
利用同角三角函数关系求得的值,再利用正弦定理先求出.
【详解】
由题意知,所以为锐角,且,
又,,
,
在中,由正弦定理得,
即,所以,
故答案为:.
【点睛】
本题考查正弦定理在解三角形中的应用,涉及同角三角函数的关系,难度较易.
(1)已知三角形的两角与其中一角的对边,解三角形时只需要求得两角的正弦值,然后代入正弦定理即可得解;
(2)已知三角形的两角及第三边时,要先利用两角和的三角函数公式求得另一角的正弦值,然后再利用正弦定理求解.
15.
【分析】
利用三角形面积公式和余弦定理可求得,由同角三角函数关系可求得结果.
【详解】
,,,
又,,,.
故答案为:.
16.
【分析】
设,在中,利用正弦定理得,由余弦定理得,然后在中,由余弦定理得(其中),从而可求出的最小值
【详解】
设,在中,由正弦定理得,即
整理得.
由余弦定理得,
因为,所以.
在中,
由余弦定理得
(其中),
所以当时,.
故答案为:
【点睛】
关键点点睛:此题考查正弦定理和余弦定理的应用,解题的关键是在中,求出和,其中,再在中,利用余弦定理表示出,从而可求得结果,考查计算能力,属于中档题
17.(Ⅰ)的周长为5;.
(Ⅱ)
.
【解析】
分析:(I)利用余弦定理表示出的平方,把的值代入求出的值,从而求出三角形的周长;
(II)根据的值,利用同角三角函数间的基本关系求出的值,利用正弦定理即可求出的值,根据大边对大角,可得为锐角,利用同角三角函数间的基本关系求出 的值,然后利用两角差的余弦函数公式化简所求的式子,把各自的值代入即可求出值.
详解:(I)
的周长为
(II) 由正弦定理
,故为锐角.则
.
点睛:本题主要考查三角函数的基本公式和解斜三角形的基础知识,同时考查学生的基本运算能力,是一道基础题.
18.(1);(2)无最小值,时取得最大值为
【分析】
(1)由三角形面积公式结合题中条件可求出的范围,进而可求出结果;
(2)先化简,再根据(1)的结果,结合正弦函数的性质即可求出结果.
【详解】
解:(1)由三角形面积公式可得,又
则,
;
(2)由题意,
无最小值,时取得最大值为.
【点睛】
本题主要考查三角函数的性质,熟记正弦函数的性质即可,属于常考题型.
19.(1);(2).
【分析】
(1)根据正弦定理,由题中条件,求出外接圆的半径,进而可求出;
(2)先由(1)求出,根据余弦定理,求出的值,并检验,再由三角形面积公式,即可得出结果.
【详解】
(1)根据正弦定理,由可化为(其中为外接圆半径),
因为,,所以,
则;
(2)因为为锐角三角形,所,
由余弦定理可得:,即,
解得或,
当时,,此时为钝角,舍去.
所以,则.
20.(1);(2)当时,的最大值为.
【分析】
(1)先由余弦定理得,再由三角形面积公式可得函数关系.
(2)由(1)所得函数关系,整理后得正弦型函数关系,可得最值.
【详解】
解:(1),
∴中,,
∵为正三角形
∴
∴四边形的面积为
,其中
(2)由(1)得,当时,
即时,的最大值为.
【点睛】
本题为三角应用题,考查余弦定理及面积公式,属于基础题.
21.(1);(2)最大值为4.
【分析】
(1)利用正弦定理和三角函数的和差公式可得答案;
(2)由可求出,然后,然后可得答案.
【详解】
(1)∵,
∴,
∴,
∵,∴,
∴,∴.
(2)设的外接圆半径为R,∵,
∴,
∴
.
∵,∴,
当,即时,,即的最大值为4
22.(1);(2)1;(3).
【分析】
(1)根据,利用余弦定理求解.
(2)由,结合余弦定理得到,再利用基本不等式求解.
(3)由正弦定理,转化为,利用两角和与差的三角函数的三角函数求解.
【详解】
(1)∵中,,
∵,
∴由余弦定理得:,
∵,
∴;
(2)因为,由余弦定理得,
又∵(当且仅当时取等号),
∴,当且仅当时,取等号
所以取得最大值为;
(3)由正弦定理,得,
∴
,
∵
,
∴
【点睛】
方法点睛:在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息,一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到,解题中注意三角形内角和定理的应用及角的范围限制.
