沪科版(2012)初中数学九年级上册 21.1 专题四 二次函数综合问题 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级上册 21.1 专题四 二次函数综合问题 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 13:46:27 | ||
图片预览

文档简介
专题四 二次函数综合问题
教学目标:
知识与技能:
1、掌握用待定系数法求二次函数解析式。
2、掌握二次函数的图像与性质的应用。
3、掌握二次函数与几何图形的综合应用。
4、掌握二次函数的实际应用,能熟练求某一变量的值或最值问题。
过程与方法:通过教学思考探究掌握二次函数与几何图形的综合应用。
情感态度与价值观:在二次函数实际应用中,知道生活中处处有数学知识。
教学重难点:
重点:二次函数的图像与性质的应用,二次函数的实际应用,能熟练求某一变量的值或最值问题。
难点:掌握二次函数与几何图形的综合应用。
教学方法:引导交流,合作探究。
教学时间:1课时
教学过程:
一.导入新课
近五年来,二次函数问题是安徽中考的必考考点之一,多数以解答题的形式出现,有时也出现在选择题中.类型主要涉及二次函数的实际应用、二次函数与几何图形的综合,或较简单的直接利用二次函数图象与性质进行求解的解答题.
探究新知:
(一)、二次函数的图象与性质的直接应用
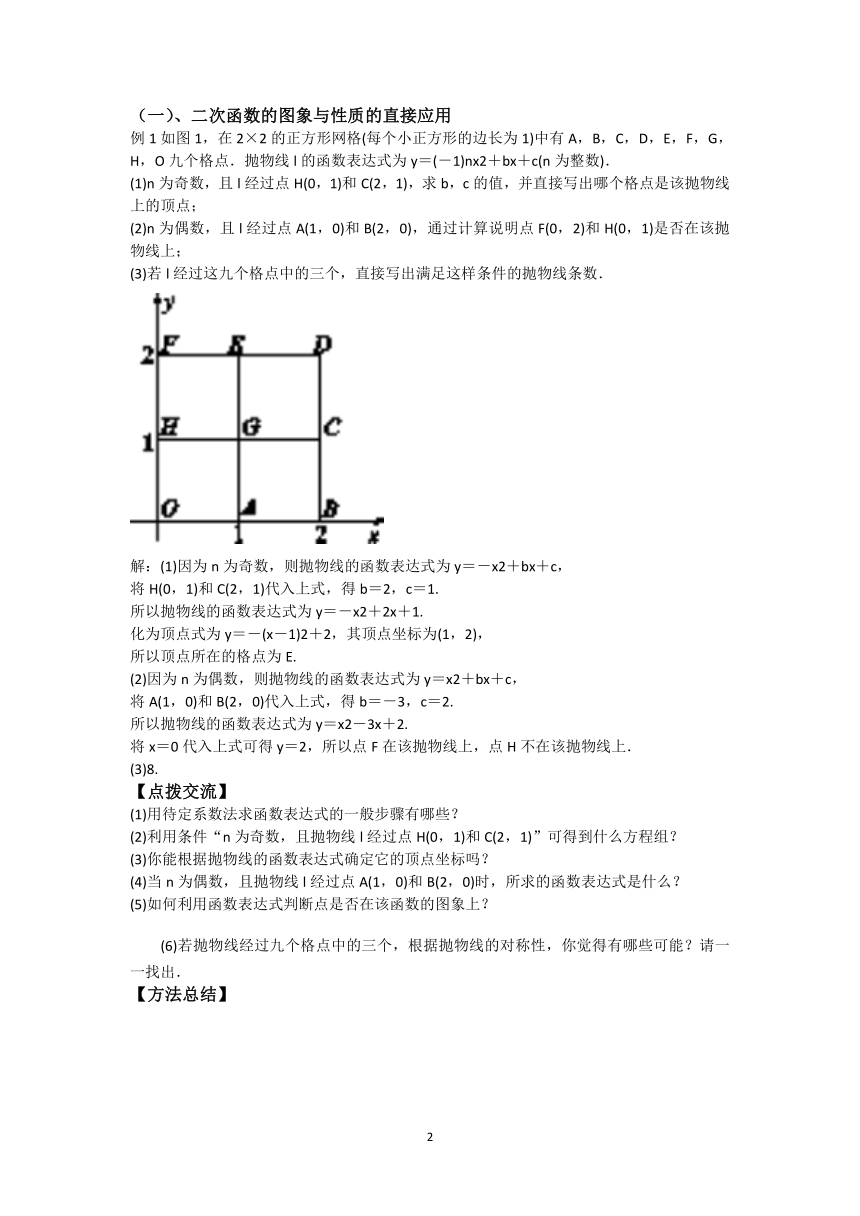
例1如图1,在2×2的正方形网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的函数表达式为y=(-1)nx2+bx+c(n为整数).
(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1,0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在该抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
解:(1)因为n为奇数,则抛物线的函数表达式为y=-x2+bx+c,
将H(0,1)和C(2,1)代入上式,得b=2,c=1.
所以抛物线的函数表达式为y=-x2+2x+1.
化为顶点式为y=-(x-1)2+2,其顶点坐标为(1,2),
所以顶点所在的格点为E.
(2)因为n为偶数,则抛物线的函数表达式为y=x2+bx+c,
将A(1,0)和B(2,0)代入上式,得b=-3,c=2.
所以抛物线的函数表达式为y=x2-3x+2.
将x=0代入上式可得y=2,所以点F在该抛物线上,点H不在该抛物线上.
(3)8.
【点拨交流】
(1)用待定系数法求函数表达式的一般步骤有哪些?
(2)利用条件“n为奇数,且抛物线l经过点H(0,1)和C(2,1)”可得到什么方程组?
(3)你能根据抛物线的函数表达式确定它的顶点坐标吗?
(4)当n为偶数,且抛物线l经过点A(1,0)和B(2,0)时,所求的函数表达式是什么?
(5)如何利用函数表达式判断点是否在该函数的图象上?
(6)若抛物线经过九个格点中的三个,根据抛物线的对称性,你觉得有哪些可能?请一一找出.
【方法总结】
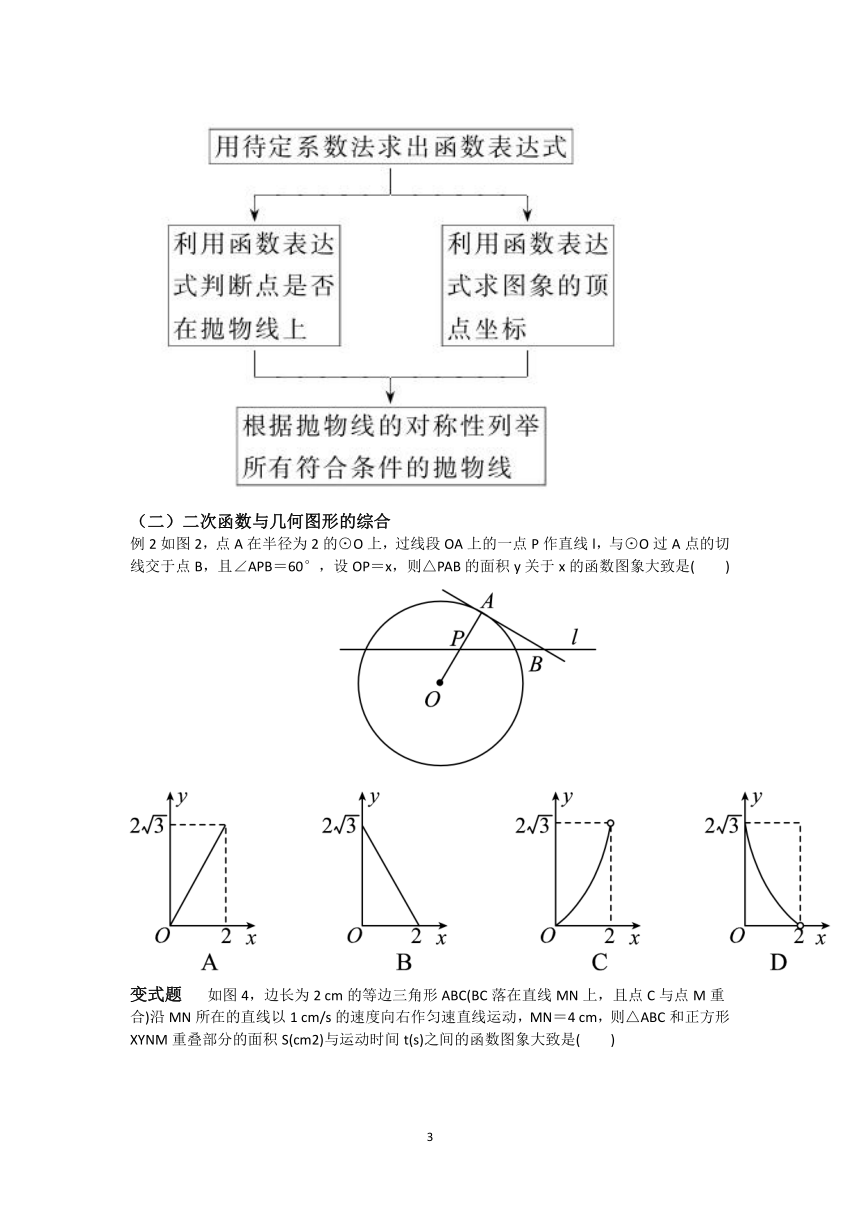
(二)二次函数与几何图形的综合
例2如图2,点A在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
变式题
如图4,边长为2
cm的等边三角形ABC(BC落在直线MN上,且点C与点M重合)沿MN所在的直线以1
cm/s的速度向右作匀速直线运动,MN=4
cm,则△ABC和正方形XYNM重叠部分的面积S(cm2)与运动时间t(s)之间的函数图象大致是( )
【点拨交流】
(1)圆的切线有什么性质?由AB是⊙O的切线可得到什么结论?
(2)已知⊙O的半径为2,设OP=x,则AP如何用含x的代数式来表示?
(3)如何利用∠APB=60°这个条件用含x的代数式表示线段AB的长?
(4)你能利用三角形面积公式得到y关于x的函数表达式吗?
(5)你能根据函数表达式知道函数的图象和性质并选择出正确的图象吗?
【方法总结】
(三)二次函数的实际应用
例3
某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数表达式;
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
【点拨交流】
(1)第(1)问涉及哪几个变量?它们之间有什么函数关系?其中哪个量是已知的?将已知量代入后得到了什么?
(2)利润和哪些量有关?它们的基本数量关系是什么?你能根据这几个量之间的数量关系列出函数表达式吗?
(3)如何根据所求得的函数表达式,利用函数的增减性求出最大利润?
【方法总结】
布置作业
系统总复习相关习题
四、板书设计
专题四
二次函数综合问题
例1、-------------------
例2.-------------------------
例3.------------------------
总结:--------------------
教学反思:
近五年来,二次函数问题是安徽中考的必考考点之一,多数以解答题的形式出现,有时也出现在选择题中.类型主要涉及二次函数的实际应用、二次函数与几何图形的综合,或较简单的直接利用二次函数图象与性质进行求解的解答题.通过这节课的教学,同学们更好地掌握二次函数的图像、性质、实际应用及二次函数与几何图形的综合应用。通过习题反馈,本节课教学效果很好。
教学目标:
知识与技能:
1、掌握用待定系数法求二次函数解析式。
2、掌握二次函数的图像与性质的应用。
3、掌握二次函数与几何图形的综合应用。
4、掌握二次函数的实际应用,能熟练求某一变量的值或最值问题。
过程与方法:通过教学思考探究掌握二次函数与几何图形的综合应用。
情感态度与价值观:在二次函数实际应用中,知道生活中处处有数学知识。
教学重难点:
重点:二次函数的图像与性质的应用,二次函数的实际应用,能熟练求某一变量的值或最值问题。
难点:掌握二次函数与几何图形的综合应用。
教学方法:引导交流,合作探究。
教学时间:1课时
教学过程:
一.导入新课
近五年来,二次函数问题是安徽中考的必考考点之一,多数以解答题的形式出现,有时也出现在选择题中.类型主要涉及二次函数的实际应用、二次函数与几何图形的综合,或较简单的直接利用二次函数图象与性质进行求解的解答题.
探究新知:
(一)、二次函数的图象与性质的直接应用
例1如图1,在2×2的正方形网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的函数表达式为y=(-1)nx2+bx+c(n为整数).
(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1,0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在该抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
解:(1)因为n为奇数,则抛物线的函数表达式为y=-x2+bx+c,
将H(0,1)和C(2,1)代入上式,得b=2,c=1.
所以抛物线的函数表达式为y=-x2+2x+1.
化为顶点式为y=-(x-1)2+2,其顶点坐标为(1,2),
所以顶点所在的格点为E.
(2)因为n为偶数,则抛物线的函数表达式为y=x2+bx+c,
将A(1,0)和B(2,0)代入上式,得b=-3,c=2.
所以抛物线的函数表达式为y=x2-3x+2.
将x=0代入上式可得y=2,所以点F在该抛物线上,点H不在该抛物线上.
(3)8.
【点拨交流】
(1)用待定系数法求函数表达式的一般步骤有哪些?
(2)利用条件“n为奇数,且抛物线l经过点H(0,1)和C(2,1)”可得到什么方程组?
(3)你能根据抛物线的函数表达式确定它的顶点坐标吗?
(4)当n为偶数,且抛物线l经过点A(1,0)和B(2,0)时,所求的函数表达式是什么?
(5)如何利用函数表达式判断点是否在该函数的图象上?
(6)若抛物线经过九个格点中的三个,根据抛物线的对称性,你觉得有哪些可能?请一一找出.
【方法总结】
(二)二次函数与几何图形的综合
例2如图2,点A在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
变式题
如图4,边长为2
cm的等边三角形ABC(BC落在直线MN上,且点C与点M重合)沿MN所在的直线以1
cm/s的速度向右作匀速直线运动,MN=4
cm,则△ABC和正方形XYNM重叠部分的面积S(cm2)与运动时间t(s)之间的函数图象大致是( )
【点拨交流】
(1)圆的切线有什么性质?由AB是⊙O的切线可得到什么结论?
(2)已知⊙O的半径为2,设OP=x,则AP如何用含x的代数式来表示?
(3)如何利用∠APB=60°这个条件用含x的代数式表示线段AB的长?
(4)你能利用三角形面积公式得到y关于x的函数表达式吗?
(5)你能根据函数表达式知道函数的图象和性质并选择出正确的图象吗?
【方法总结】
(三)二次函数的实际应用
例3
某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数表达式;
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
【点拨交流】
(1)第(1)问涉及哪几个变量?它们之间有什么函数关系?其中哪个量是已知的?将已知量代入后得到了什么?
(2)利润和哪些量有关?它们的基本数量关系是什么?你能根据这几个量之间的数量关系列出函数表达式吗?
(3)如何根据所求得的函数表达式,利用函数的增减性求出最大利润?
【方法总结】
布置作业
系统总复习相关习题
四、板书设计
专题四
二次函数综合问题
例1、-------------------
例2.-------------------------
例3.------------------------
总结:--------------------
教学反思:
近五年来,二次函数问题是安徽中考的必考考点之一,多数以解答题的形式出现,有时也出现在选择题中.类型主要涉及二次函数的实际应用、二次函数与几何图形的综合,或较简单的直接利用二次函数图象与性质进行求解的解答题.通过这节课的教学,同学们更好地掌握二次函数的图像、性质、实际应用及二次函数与几何图形的综合应用。通过习题反馈,本节课教学效果很好。
