沪科版(2012)初中数学九年级上册 21.4.1 二次函数的最值问题教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级上册 21.4.1 二次函数的最值问题教案 |  | |
| 格式 | zip | ||
| 文件大小 | 254.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 13:50:16 | ||
图片预览

文档简介
《二次函数的最值问题》教案设计
教学目标
会结合图像与函数的知识进行分类讨论,求解一元二次函数的最值问题,提高学生的综合能力,培养学生良好的思维习惯,加深对数形结合、分类讨论等数学思想的认识。
2、了解图像与函数的关系,进一步感受数形结合的基本思想。
3、经历从“定轴定区间”到“定轴动区间”到“动轴定区间”的类比推理,培养学生类比推理能力;使学生养成积极思考,独立思考的好习惯,并且同时培养学生的团队合作精神。
4、通过将“二次函数的最值”的知识灵活运用于实际,让学生体会到学习数学的价值,从而提高学生学习数学的兴趣。
二、教学重难点
教学重点:区间范围内二次函数的最值问题的解决方法,实际问题中的函数最值问题分析;
教学难点:“动轴定区间”、“动轴定区间”的最值问题的解题分析
三、教学方法
类比推理、讲授发现
教学过程
(一)复习旧知
提问:九年级数学中经常会遇到求函数最值的问题,尤其是二次函数的最值问题最为突出。在学习过程中你遇到过哪些与二次函数最值有关的题型呢?
学生可能会回答:实际问题中的二次函数最值、纯函数最值......
(二)揭示课题
1、提问:那么在求函数最值的过程中,我们最应该关注的是什么因素?
引导学生回答“自变量的具体取值范围”
那我们一起来看看自变量不同取值范围内的函数最值问题,从而自然引出课题《二次函数的最值问题》
2、例1:二次函数y=(x^2)+2x-3当-4≤
x
≤0时的最大值及最小值分别是多少?
分析:例1是最基本的题型,学生可以自己完成。对于定轴定区间类的函数最值问题,我们只需要根据函数性质,结合函数图像,分析在区间内的函数图像的最高点和最低点,代入相应坐标,即可求出。
变式一:二次函数y=(x^2)-2ax-3当-4≤
x
≤0时的最小值是多少?
分析:变式1是难度较大的题型涉及到分类讨论以及字母的推理运算。教师要借助几何画板引导学生观察出函数对称轴在变化,二次函数在定区间-4≤
x
≤0上的图像也随着变化,从而影响到最值.教师注意和学生互动讨论.学生对于是关于参数的函数较难理解,教师要注意用函数概念加以说明,此处也是让学生对函数概念螺旋式上升理解的一个具体例子.
学生讨论归纳变式1的解题方法和规律时教师要引导学生注意分类讨论思想的应用.
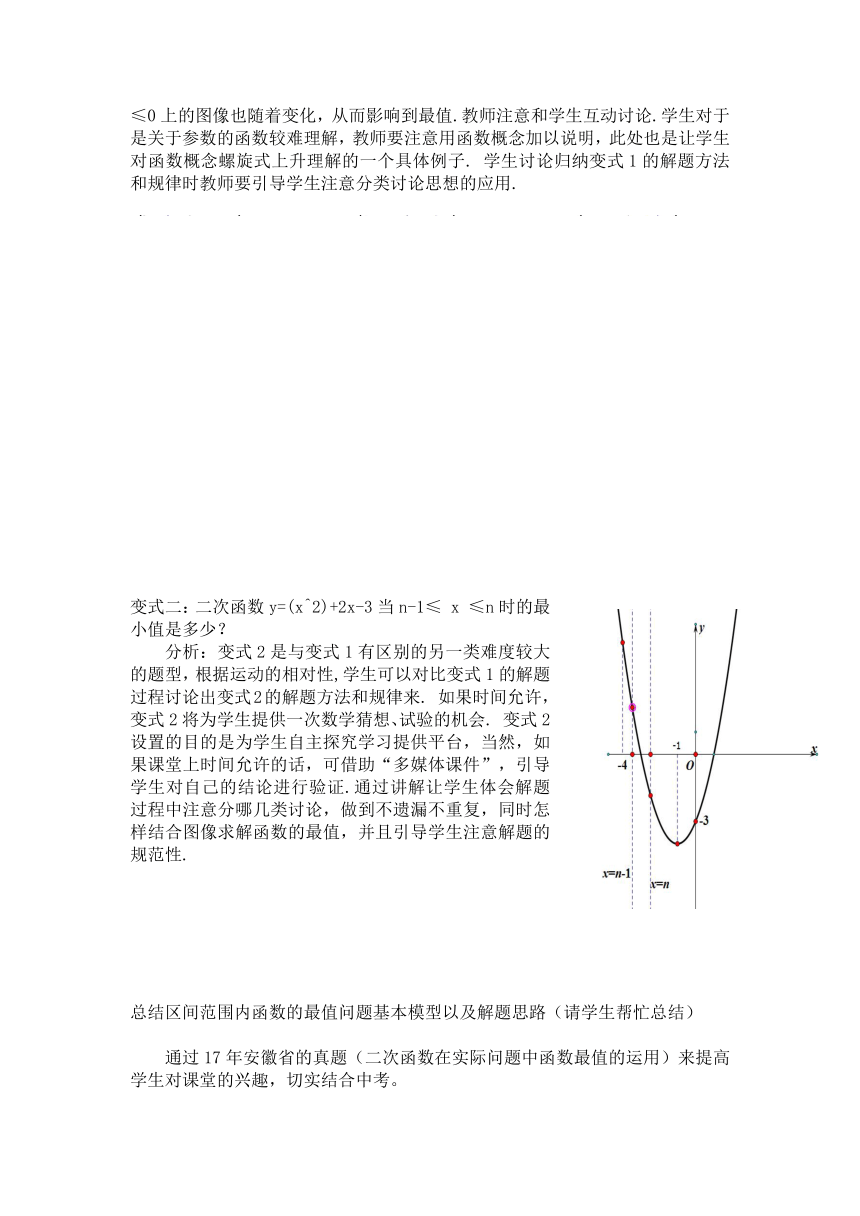
变式二:二次函数y=(x^2)+2x-3当n-1≤
x
≤n时的最小值是多少?
分析:变式2是与变式1有区别的另一类难度较大的题型,根据运动的相对性,学生可以对比变式1的解题过程讨论出变式2的解题方法和规律来.
如果时间允许,变式2将为学生提供一次数学猜想、试验的机会.
变式2设置的目的是为学生自主探究学习提供平台,当然,如果课堂上时间允许的话,可借助“多媒体课件”,引导学生对自己的结论进行验证.通过讲解让学生体会解题过程中注意分哪几类讨论,做到不遗漏不重复,同时怎样结合图像求解函数的最值,并且引导学生注意解题的规范性.
总结区间范围内函数的最值问题基本模型以及解题思路(请学生帮忙总结)
通过17年安徽省的真题(二次函数在实际问题中函数最值的运用)来提高学生对课堂的兴趣,切实结合中考。
例二:某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与售价x(元/千克)满足一次函数关系,部分数据如下表:
售价x(元/每千克)
50
60
70
销售量y(千克)
100
80
60
求y与x之间的函数表达式;
分析:审清题目,明确函数解析式的类型,合理的设一般式,规范解题过程,时间足够的情况下可以请学生上台板演。
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式;(利润=收入
—
成本);
分析:根据已给的利润计算方式,建立合适的函数模型,在此问解答时要注意是否写上自变量的取值范围,解析式是否要化简。
(3)试说明(2)中总利润W随售价x的变化而变化情况,并指出售价为多少时获得最大利润,最大利润时多少?
分析:审清题意是解答的第一步,提问中共有几个小问题?我们需要分别怎样作答?那么结合第(2)问,对于实际问题中的二次函数模型最值,我们在求解的过程中要注意什么?怎样求最方便?结合函数图像和取值范围快速的判断,图像可以画简图。
(三)链接中考
小结作业
通过本节课的学习,你有哪些收获?
学生总结,教师补充
板书设计
二次函数的最值问题
区间范围内的最值问题
定轴定区间
动轴定区间
例题
定轴动区间
学生练习
分类:对称轴与区间位置关系
实际问题中的二次函数最值
(注意自变量的取值范围、取整)
七、教学反思
教学目标
会结合图像与函数的知识进行分类讨论,求解一元二次函数的最值问题,提高学生的综合能力,培养学生良好的思维习惯,加深对数形结合、分类讨论等数学思想的认识。
2、了解图像与函数的关系,进一步感受数形结合的基本思想。
3、经历从“定轴定区间”到“定轴动区间”到“动轴定区间”的类比推理,培养学生类比推理能力;使学生养成积极思考,独立思考的好习惯,并且同时培养学生的团队合作精神。
4、通过将“二次函数的最值”的知识灵活运用于实际,让学生体会到学习数学的价值,从而提高学生学习数学的兴趣。
二、教学重难点
教学重点:区间范围内二次函数的最值问题的解决方法,实际问题中的函数最值问题分析;
教学难点:“动轴定区间”、“动轴定区间”的最值问题的解题分析
三、教学方法
类比推理、讲授发现
教学过程
(一)复习旧知
提问:九年级数学中经常会遇到求函数最值的问题,尤其是二次函数的最值问题最为突出。在学习过程中你遇到过哪些与二次函数最值有关的题型呢?
学生可能会回答:实际问题中的二次函数最值、纯函数最值......
(二)揭示课题
1、提问:那么在求函数最值的过程中,我们最应该关注的是什么因素?
引导学生回答“自变量的具体取值范围”
那我们一起来看看自变量不同取值范围内的函数最值问题,从而自然引出课题《二次函数的最值问题》
2、例1:二次函数y=(x^2)+2x-3当-4≤
x
≤0时的最大值及最小值分别是多少?
分析:例1是最基本的题型,学生可以自己完成。对于定轴定区间类的函数最值问题,我们只需要根据函数性质,结合函数图像,分析在区间内的函数图像的最高点和最低点,代入相应坐标,即可求出。
变式一:二次函数y=(x^2)-2ax-3当-4≤
x
≤0时的最小值是多少?
分析:变式1是难度较大的题型涉及到分类讨论以及字母的推理运算。教师要借助几何画板引导学生观察出函数对称轴在变化,二次函数在定区间-4≤
x
≤0上的图像也随着变化,从而影响到最值.教师注意和学生互动讨论.学生对于是关于参数的函数较难理解,教师要注意用函数概念加以说明,此处也是让学生对函数概念螺旋式上升理解的一个具体例子.
学生讨论归纳变式1的解题方法和规律时教师要引导学生注意分类讨论思想的应用.
变式二:二次函数y=(x^2)+2x-3当n-1≤
x
≤n时的最小值是多少?
分析:变式2是与变式1有区别的另一类难度较大的题型,根据运动的相对性,学生可以对比变式1的解题过程讨论出变式2的解题方法和规律来.
如果时间允许,变式2将为学生提供一次数学猜想、试验的机会.
变式2设置的目的是为学生自主探究学习提供平台,当然,如果课堂上时间允许的话,可借助“多媒体课件”,引导学生对自己的结论进行验证.通过讲解让学生体会解题过程中注意分哪几类讨论,做到不遗漏不重复,同时怎样结合图像求解函数的最值,并且引导学生注意解题的规范性.
总结区间范围内函数的最值问题基本模型以及解题思路(请学生帮忙总结)
通过17年安徽省的真题(二次函数在实际问题中函数最值的运用)来提高学生对课堂的兴趣,切实结合中考。
例二:某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与售价x(元/千克)满足一次函数关系,部分数据如下表:
售价x(元/每千克)
50
60
70
销售量y(千克)
100
80
60
求y与x之间的函数表达式;
分析:审清题目,明确函数解析式的类型,合理的设一般式,规范解题过程,时间足够的情况下可以请学生上台板演。
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式;(利润=收入
—
成本);
分析:根据已给的利润计算方式,建立合适的函数模型,在此问解答时要注意是否写上自变量的取值范围,解析式是否要化简。
(3)试说明(2)中总利润W随售价x的变化而变化情况,并指出售价为多少时获得最大利润,最大利润时多少?
分析:审清题意是解答的第一步,提问中共有几个小问题?我们需要分别怎样作答?那么结合第(2)问,对于实际问题中的二次函数模型最值,我们在求解的过程中要注意什么?怎样求最方便?结合函数图像和取值范围快速的判断,图像可以画简图。
(三)链接中考
小结作业
通过本节课的学习,你有哪些收获?
学生总结,教师补充
板书设计
二次函数的最值问题
区间范围内的最值问题
定轴定区间
动轴定区间
例题
定轴动区间
学生练习
分类:对称轴与区间位置关系
实际问题中的二次函数最值
(注意自变量的取值范围、取整)
七、教学反思
