沪教版(上海)九年级数学上册第26章二次函数单元同步重难点复习卷(word版含答案)
文档属性
| 名称 | 沪教版(上海)九年级数学上册第26章二次函数单元同步重难点复习卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 354.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 13:10:50 | ||
图片预览


文档简介
沪教版(上海)九年级数学上册第26章二次函数单元同步重难点复习卷
一、单选题
1.如果函数是二次函数,则的取值范围是(
)
A.
B.
C.=﹣2
D.为全体实数
2.将抛物线按以下方法平移可以得到抛物线的是(
)
A.向左平移2个单位,向下平移3个单位
B.向左平移3个单位,向上平移2个单位
C.向右平移3个单位,向上平移2个单位
D.向右平移3个单位,向下平移2个单位
3.设函数,,若当时,,则(
)
A.当时,
B.当时,
C.当时,
D.当时,
4.抛物线与x轴的交点坐标为,则代数式的值为(
)
A.2033
B.2012
C.2026
D.2005
5.若二次函数y=﹣x2+x+c的图象与x轴没有交点,则二次函数y=﹣x2+x+c的图象与反比例函数y=的图象的交点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),下列四个结论:①如果点(,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④;其中正确的有( )
A.4个
B.3个
C.2个
D.1个
7.某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是(
)
A.14元
B.15元
C.16元
D.18元
8.如图,抛物线与轴交于点,对称轴为,则下列结论中正确的是(
)
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
9.如图是抛物线y=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,4),与x轴的一个交点是B(3,0),下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=4有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣2.0);⑤x(ax+b)≤a+b,其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
10.如图,已知二次函数的图象如图所示,有下列5个结论 ;;;;的实数其中正确结论的有
A.
B.
C.
D.
11.抛物线y=ax?+bx+c(a>0)与直线y=bx+c在同一坐标系中的大致图像可能为(
)
A.
B.
C.
D.
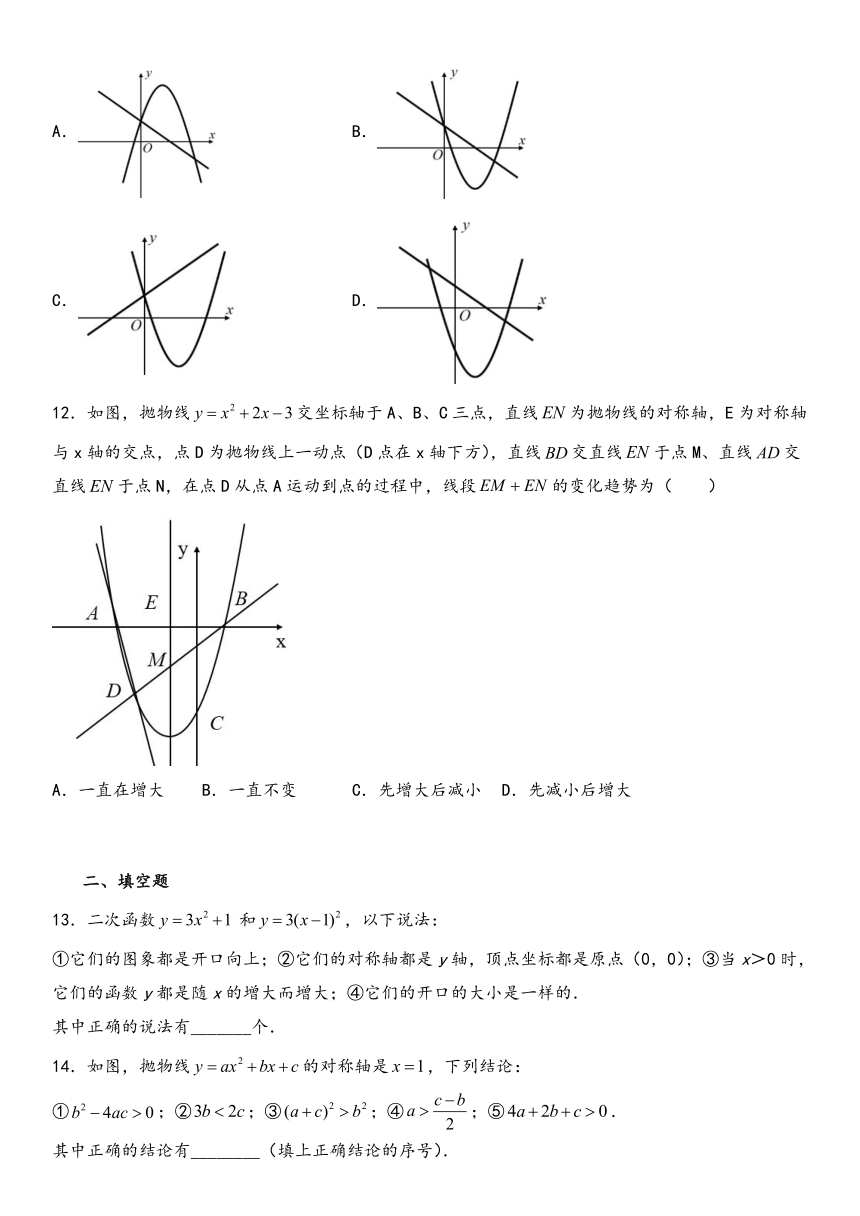
12.如图,抛物线交坐标轴于A、B、C三点,直线为抛物线的对称轴,E为对称轴与x轴的交点,点D为抛物线上一动点(D点在x轴下方),直线交直线于点M、直线交直线于点N,在点D从点A运动到点的过程中,线段的变化趋势为(
)
A.一直在增大
B.一直不变
C.先增大后减小
D.先减小后增大
二、填空题
13.二次函数?和,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
14.如图,抛物线的对称轴是,下列结论:
①;②;③;④;⑤.
其中正确的结论有________(填上正确结论的序号).
15.二次函数y=2x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.
16.(2017届河南省周口市西华县中招第二次模拟考试数学试卷)已知y=?x2?3x+4(?10≤x≤0)的图象上有一动点P,点P的纵坐标为整数值时,记为“好点”,则“好点”的个数为__________.
17.甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为,羽毛球飞行的水平距离(米)与其距地面高度(米)之间的关系式为,如图,已知球网距原点米,乙(用线段表示)扣球的最大高度为米,设乙的起跳点的横坐标为,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则的取值范围是__________.
三、解答题
18.抛物线y=ax2与直线y=2x-3交于点A(1,b).
(1)求a,b的值;
(2)求抛物线y=ax2与直线y=-2的两个交点B,C的坐标(B点在C点右侧);
(3)求△OBC的面积.
19.某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.
已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴,
AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.
20.如图,抛物线与轴交于、两点,与轴交于点,且,.
(1)求抛物线的解析式;
(2)已知抛物线上点的横坐标为,在抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
21.如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
22.定义:在平面直角坐标系xOy中,直线y=a(x﹣m)+k称为抛物线y=a(x﹣m)2+k的关联直线.
(1)求抛物线y=x2+6x﹣1的关联直线;
(2)已知抛物线y=ax2+bx+c与它的关联直线y=2x+3都经过y轴上同一点,求这条抛物线的表达式;
(3)如图,顶点在第一象限的抛物线y=﹣a(x﹣1)2+4a与它的关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,连结AC、BC.当△ABC为直角三角形时,求a的值.
23.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)、B(4,0)两点,与y轴交于点C,且OC=3OA.点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
(1)求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,求过点P作PF⊥BC于点F,试问△PDF的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四边形CDPQ是否成为菱形?如果能,请求出此时点P的坐标,如果不能,请说明理由.
试卷第1页,总3页
参考答案
1.C2.C3.D4.D5.D6.A7.C8.D9.B10.B11.B12.B13.2
14.①②④
15.
16.14
17.
18.(1)a=
-1
b=
-1
(2)
B(-2)
C(
--2)
(3)面积是2
19.(1)y=x2+8(-16≤x≤16);(2)20;(3)①3.5米;②在离桥的一端4米处,抛物线型桥墩高3.5米;
圆弧型桥墩高4米.
20.(1);(2)存在,点.
21.(1)
y=x2-3x
;(2)m=4,D(2,-2).
22.(1)y=x+3﹣10=x﹣7;(2)y=2x2+3或y=2(x+1)2+1;(3)a=1或a=.
23.(1)
y=﹣+x+3;(2)
有最大值,;(3)
存在这样的Q点,使得四边形CDPQ是菱形,此时点P的坐标为(,)或(,﹣).
一、单选题
1.如果函数是二次函数,则的取值范围是(
)
A.
B.
C.=﹣2
D.为全体实数
2.将抛物线按以下方法平移可以得到抛物线的是(
)
A.向左平移2个单位,向下平移3个单位
B.向左平移3个单位,向上平移2个单位
C.向右平移3个单位,向上平移2个单位
D.向右平移3个单位,向下平移2个单位
3.设函数,,若当时,,则(
)
A.当时,
B.当时,
C.当时,
D.当时,
4.抛物线与x轴的交点坐标为,则代数式的值为(
)
A.2033
B.2012
C.2026
D.2005
5.若二次函数y=﹣x2+x+c的图象与x轴没有交点,则二次函数y=﹣x2+x+c的图象与反比例函数y=的图象的交点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),下列四个结论:①如果点(,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④;其中正确的有( )
A.4个
B.3个
C.2个
D.1个
7.某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是(
)
A.14元
B.15元
C.16元
D.18元
8.如图,抛物线与轴交于点,对称轴为,则下列结论中正确的是(
)
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
9.如图是抛物线y=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,4),与x轴的一个交点是B(3,0),下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=4有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣2.0);⑤x(ax+b)≤a+b,其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
10.如图,已知二次函数的图象如图所示,有下列5个结论 ;;;;的实数其中正确结论的有
A.
B.
C.
D.
11.抛物线y=ax?+bx+c(a>0)与直线y=bx+c在同一坐标系中的大致图像可能为(
)
A.
B.
C.
D.
12.如图,抛物线交坐标轴于A、B、C三点,直线为抛物线的对称轴,E为对称轴与x轴的交点,点D为抛物线上一动点(D点在x轴下方),直线交直线于点M、直线交直线于点N,在点D从点A运动到点的过程中,线段的变化趋势为(
)
A.一直在增大
B.一直不变
C.先增大后减小
D.先减小后增大
二、填空题
13.二次函数?和,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
14.如图,抛物线的对称轴是,下列结论:
①;②;③;④;⑤.
其中正确的结论有________(填上正确结论的序号).
15.二次函数y=2x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.
16.(2017届河南省周口市西华县中招第二次模拟考试数学试卷)已知y=?x2?3x+4(?10≤x≤0)的图象上有一动点P,点P的纵坐标为整数值时,记为“好点”,则“好点”的个数为__________.
17.甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为,羽毛球飞行的水平距离(米)与其距地面高度(米)之间的关系式为,如图,已知球网距原点米,乙(用线段表示)扣球的最大高度为米,设乙的起跳点的横坐标为,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则的取值范围是__________.
三、解答题
18.抛物线y=ax2与直线y=2x-3交于点A(1,b).
(1)求a,b的值;
(2)求抛物线y=ax2与直线y=-2的两个交点B,C的坐标(B点在C点右侧);
(3)求△OBC的面积.
19.某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.
已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴,
AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.
20.如图,抛物线与轴交于、两点,与轴交于点,且,.
(1)求抛物线的解析式;
(2)已知抛物线上点的横坐标为,在抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
21.如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
22.定义:在平面直角坐标系xOy中,直线y=a(x﹣m)+k称为抛物线y=a(x﹣m)2+k的关联直线.
(1)求抛物线y=x2+6x﹣1的关联直线;
(2)已知抛物线y=ax2+bx+c与它的关联直线y=2x+3都经过y轴上同一点,求这条抛物线的表达式;
(3)如图,顶点在第一象限的抛物线y=﹣a(x﹣1)2+4a与它的关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,连结AC、BC.当△ABC为直角三角形时,求a的值.
23.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)、B(4,0)两点,与y轴交于点C,且OC=3OA.点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
(1)求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,求过点P作PF⊥BC于点F,试问△PDF的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四边形CDPQ是否成为菱形?如果能,请求出此时点P的坐标,如果不能,请说明理由.
试卷第1页,总3页
参考答案
1.C2.C3.D4.D5.D6.A7.C8.D9.B10.B11.B12.B13.2
14.①②④
15.
16.14
17.
18.(1)a=
-1
b=
-1
(2)
B(-2)
C(
--2)
(3)面积是2
19.(1)y=x2+8(-16≤x≤16);(2)20;(3)①3.5米;②在离桥的一端4米处,抛物线型桥墩高3.5米;
圆弧型桥墩高4米.
20.(1);(2)存在,点.
21.(1)
y=x2-3x
;(2)m=4,D(2,-2).
22.(1)y=x+3﹣10=x﹣7;(2)y=2x2+3或y=2(x+1)2+1;(3)a=1或a=.
23.(1)
y=﹣+x+3;(2)
有最大值,;(3)
存在这样的Q点,使得四边形CDPQ是菱形,此时点P的坐标为(,)或(,﹣).
