沪科版(2012)初中数学七年级下册 10.4 平移 教案
文档属性
| 名称 | 沪科版(2012)初中数学七年级下册 10.4 平移 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览


文档简介
10.4
平移
教学目标
1、知识与技能
理解平移变换的基本特征:对应点连线平行且相等。
2、过程与方法
经历观察、分析、操作、概括等过程,进而认识平移的性质。
3、情感、态度与价值观
进一步发展空间观念,增强审美意识。
教学重难点
重点
平移的概念及其性质。
难点
探索平移的性质。
教学过程
一、平移的概念
问题1:如何在一张半透明的纸上,画出一排形状和大小如图的胡巴呢?
“胡巴”的形状、大小、位置在运动前后是否发生了变化?
生:形状不变,大小不变,位置改变。
平移概念:在平面内,将一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
平移时,原图形上的所有点都沿同一个方向移动相同的距离。如下图,原图形上一点A平移后成为点D,这样的两点叫做对应点。
练一练:
判断下面几组图形变换是不是平移?
思考:图形平移的方向一定是水平方向吗?
生:图形平移的方向不一定是水平方向。
师;是的,图形平移的方向不一定是水平方向,如下图;
问题2:观察以下几种生活现象,想一想平移是由什么决定的?
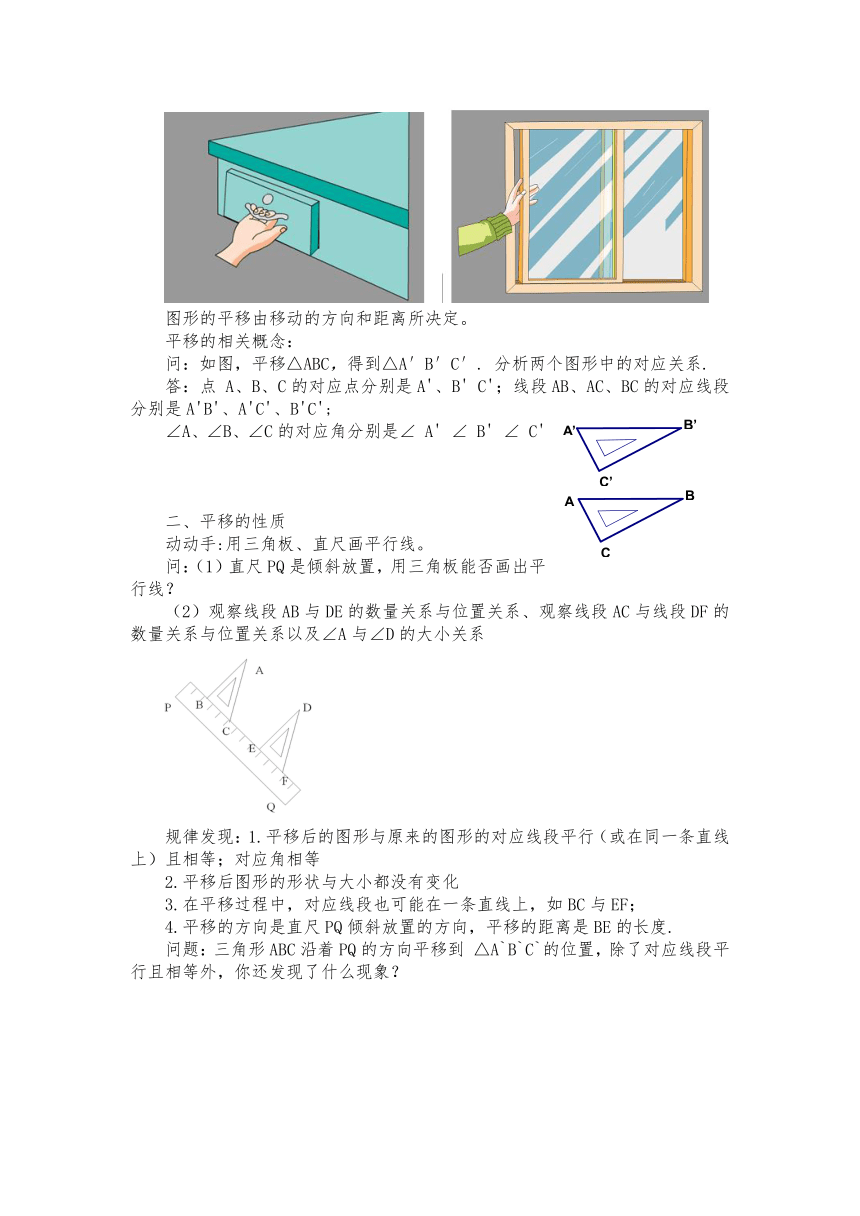
图形的平移由移动的方向和距离所决定。
平移的相关概念:
问:如图,平移△ABC,得到△A′B′C′.
分析两个图形中的对应关系.
答:点
A、B、C的对应点分别是A'、B'
C';线段AB、AC、BC的对应线段分别是A'B'、A'C'、B'C';
∠A、∠B、∠C的对应角分别是∠
A'
∠
B'
∠
C'
二、平移的性质
动动手:用三角板、直尺画平行线。
问:(1)直尺PQ是倾斜放置,用三角板能否画出平行线?
(2)观察线段AB与DE的数量关系与位置关系、观察线段AC与线段DF的数量关系与位置关系以及∠A与∠D的大小关系
规律发现:1.平移后的图形与原来的图形的对应线段平行(或在同一条直线上)且相等;对应角相等
2.平移后图形的形状与大小都没有变化
3.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
问题:三角形ABC沿着PQ的方向平移到
△A`B`C`的位置,除了对应线段平行且相等外,你还发现了什么现象?
图形平移的基本性质:
①平移只改变图形的位置,不改变图形的形状和大小
②对应线段平行(或在同一直线上)且相等;对应角相等
③连接各组对应点的线段互相平行(或在同一条直线上)且相等。
几何符号语言:
如图,∵
△
ABC平移得到△
DEF
∴
②
AB∥DE,AC∥DF,
BC∥EF(或共线),
AB=DE,AC=DF,BC=EF
∠A=
∠D,
∠B=
∠E,
∠C=
∠F
③AD
∥BE
∥CF且AD=BE=CF
三、例题讲解
例1
如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.,并指出平移的方向和距离.
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'
为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
例2:如图是一块长方形的草地,
长为21米.宽为15米
在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
思路点拨:两种平移方式
变式:如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
思路点拨:平移构成规则图形
四、巩固练习
1.
在图形平移中,下面说法中错误的是(
)
A.
图形上任意点移动的方向相同
B.
图形上任意点移动的距离相等
C.
图形上任意两点的连线的长度不变
D.
图形上可能存在不动点
2.如图所示,图中小正方形的边长为a,则阴影部分的面积是:________
3.平移改变的是图形的(
)
A
、位置
B
、大小
C、
形状
D
、位置、大小和形状
4.经过平移,对应点所连的线段(
)
A
、平行
B
、相等
C
、平行且相等
D、
既不平行,又不相等
5.下面
2,3,4,5
幅图中哪幅图是由1平移得到的?
6.经过平移,图形上每个点都沿同一个方向移动了一段距离.下面说法正确的是(
)
A
、不同的点移动的距离不同
B、
既可能相同也可能不同
C
、不同的点移动的距离相同
D
、无法确定
五、课堂小结
本节课的主要内容是什么?你有哪些收获?
六、作业
同步练习册10.4节
平移
教学目标
1、知识与技能
理解平移变换的基本特征:对应点连线平行且相等。
2、过程与方法
经历观察、分析、操作、概括等过程,进而认识平移的性质。
3、情感、态度与价值观
进一步发展空间观念,增强审美意识。
教学重难点
重点
平移的概念及其性质。
难点
探索平移的性质。
教学过程
一、平移的概念
问题1:如何在一张半透明的纸上,画出一排形状和大小如图的胡巴呢?
“胡巴”的形状、大小、位置在运动前后是否发生了变化?
生:形状不变,大小不变,位置改变。
平移概念:在平面内,将一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
平移时,原图形上的所有点都沿同一个方向移动相同的距离。如下图,原图形上一点A平移后成为点D,这样的两点叫做对应点。
练一练:
判断下面几组图形变换是不是平移?
思考:图形平移的方向一定是水平方向吗?
生:图形平移的方向不一定是水平方向。
师;是的,图形平移的方向不一定是水平方向,如下图;
问题2:观察以下几种生活现象,想一想平移是由什么决定的?
图形的平移由移动的方向和距离所决定。
平移的相关概念:
问:如图,平移△ABC,得到△A′B′C′.
分析两个图形中的对应关系.
答:点
A、B、C的对应点分别是A'、B'
C';线段AB、AC、BC的对应线段分别是A'B'、A'C'、B'C';
∠A、∠B、∠C的对应角分别是∠
A'
∠
B'
∠
C'
二、平移的性质
动动手:用三角板、直尺画平行线。
问:(1)直尺PQ是倾斜放置,用三角板能否画出平行线?
(2)观察线段AB与DE的数量关系与位置关系、观察线段AC与线段DF的数量关系与位置关系以及∠A与∠D的大小关系
规律发现:1.平移后的图形与原来的图形的对应线段平行(或在同一条直线上)且相等;对应角相等
2.平移后图形的形状与大小都没有变化
3.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
问题:三角形ABC沿着PQ的方向平移到
△A`B`C`的位置,除了对应线段平行且相等外,你还发现了什么现象?
图形平移的基本性质:
①平移只改变图形的位置,不改变图形的形状和大小
②对应线段平行(或在同一直线上)且相等;对应角相等
③连接各组对应点的线段互相平行(或在同一条直线上)且相等。
几何符号语言:
如图,∵
△
ABC平移得到△
DEF
∴
②
AB∥DE,AC∥DF,
BC∥EF(或共线),
AB=DE,AC=DF,BC=EF
∠A=
∠D,
∠B=
∠E,
∠C=
∠F
③AD
∥BE
∥CF且AD=BE=CF
三、例题讲解
例1
如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.,并指出平移的方向和距离.
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'
为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
例2:如图是一块长方形的草地,
长为21米.宽为15米
在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
思路点拨:两种平移方式
变式:如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
思路点拨:平移构成规则图形
四、巩固练习
1.
在图形平移中,下面说法中错误的是(
)
A.
图形上任意点移动的方向相同
B.
图形上任意点移动的距离相等
C.
图形上任意两点的连线的长度不变
D.
图形上可能存在不动点
2.如图所示,图中小正方形的边长为a,则阴影部分的面积是:________
3.平移改变的是图形的(
)
A
、位置
B
、大小
C、
形状
D
、位置、大小和形状
4.经过平移,对应点所连的线段(
)
A
、平行
B
、相等
C
、平行且相等
D、
既不平行,又不相等
5.下面
2,3,4,5
幅图中哪幅图是由1平移得到的?
6.经过平移,图形上每个点都沿同一个方向移动了一段距离.下面说法正确的是(
)
A
、不同的点移动的距离不同
B、
既可能相同也可能不同
C
、不同的点移动的距离相同
D
、无法确定
五、课堂小结
本节课的主要内容是什么?你有哪些收获?
六、作业
同步练习册10.4节
