人教版 八年级数学 下册第18章 平行四边形 综合训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学 下册第18章 平行四边形 综合训练(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 13:26:10 | ||
图片预览


文档简介
人教版
八年级数学
第18章
平行四边形
综合训练
一、选择题
1.
矩形具有而平行四边形不具有的性质为(
)
A.对角线相等
B.对角相等
C.对角线互相平分
D.对边相等
2.
如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A.
1 B.
2 C.
3 D.
4
3.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
4.
(2020·襄阳)已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是(
)
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
5.
(2020·贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是( )
A.5
B.20
C.24
D.32
6.
(2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72
B.24
C.48
D.96
7.
(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
8.
(3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
二、填空题
9.
如图,在平行四边中,,则
.
10.
已知正方形的边长是正方形的对角线,则
11.
如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是________.
12.
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
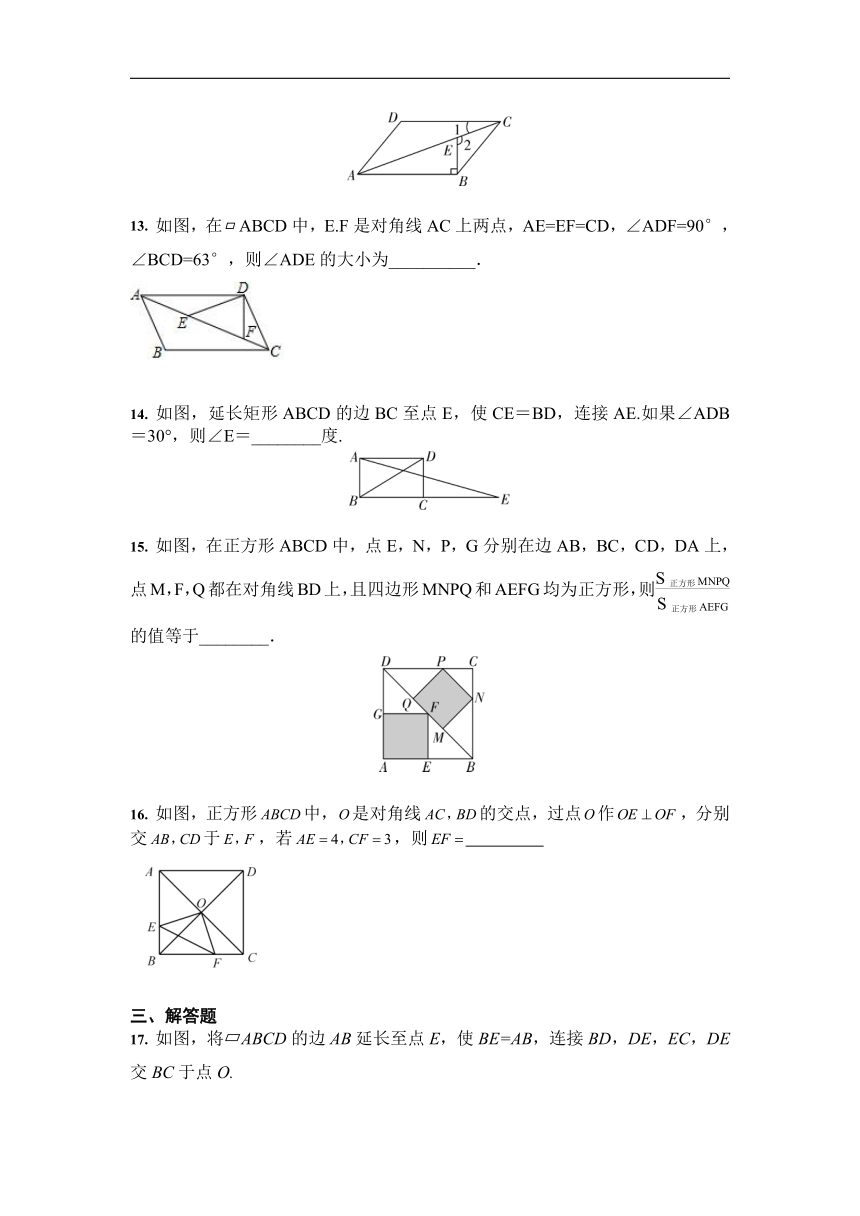
13.
如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
14.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=________度.
15.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于________.
16.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
三、解答题
17.
如图,将?ABCD的边AB延长至点E,使BE=AB,连接BD,DE,EC,DE交BC于点O.
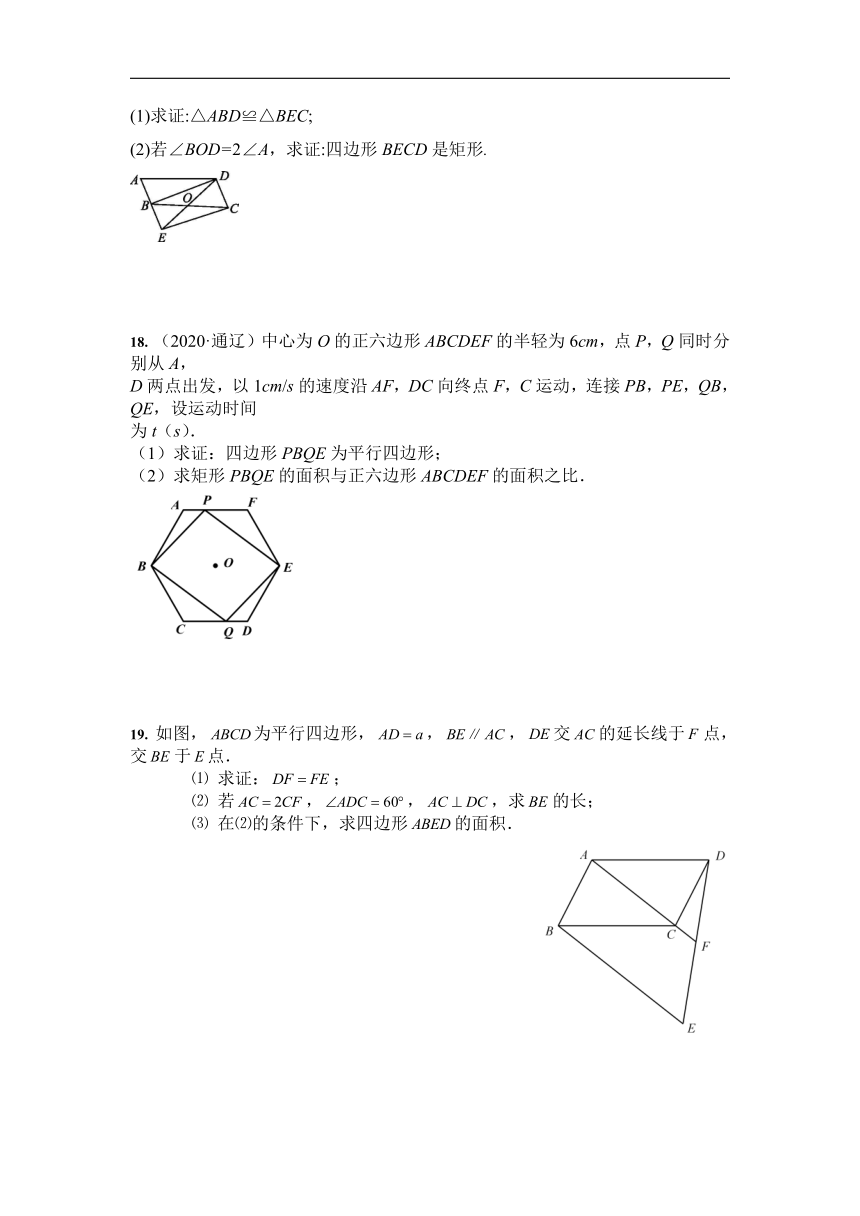
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
18.
(2020·通辽)中心为O的正六边形ABCDEF的半轻为6cm,点P,Q同时分别从A,
D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间
为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
19.
如图,为平行四边形,,,交的延长线于点,交于点.
⑴
求证:;
⑵
若,,,求的长;
⑶
在⑵的条件下,求四边形的面积.
人教版
八年级数学
第18章
平行四边形
综合训练-答案
一、选择题
1.
【答案】A
2.
【答案】C
3.
【答案】C
4.
【答案】B
5.
【答案】
B.
6.
【答案】
C
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
7.
【答案】B
8.
【答案】B
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
二、填空题
9.
【答案】
10.
【答案】
11.
【答案】24 解图
12.
【答案】110°
13.
【答案】21°
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
14.
【答案】15 解图
15.
【答案】
16.
【答案】
三、解答题
17.
【答案】
证明:(1)在?ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵BE=AB,∴BE=DC,
∴四边形BECD是平行四边形,
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知四边形BECD是平行四边形,
则OD=OE,OC=OB.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴BC=ED,
∴平行四边形BECD是矩形.
18.
【答案】
证明:(1)在正六边形ABCDEF中,AB=AF=FE=ED=DC=BC=6,∠A=∠F=∠D=∠C=120°,
∵VP=VQ=1cm/s,∴AP=DQ=t,
∵PF=AF-AP=6-t,CQ=CD-DQ=6-t,
∴PF=CQ=6-t,
在△ABP和△DQE中,
AP=DQ=t,∠A
=∠D
=120°,AB=DE=6,
∴△ABP≌△DQE,∴BP=EQ,
同理可证△PEF≌△QBC,∴PE=QB,
∴四边形PBQE为平行四边形.
(2)连结BE,CO,DO,作CG⊥BE于点G,QH⊥BE于点H.
∵四边形PBQE是矩形,∴∠BQE=90°,
∴BE是正六边形ABCDEF的外接圆直径,
即BE过点O,且BE=12,
∵ED=DC=BC=6,
∴∠EOD=∠COD=∠BOC
=60°,
又∵OE=OD=OC=OB,
∴△EOD,△COD,△BOC是全等的等边三角形,
∴CG=CO·sin∠BOC=CO·sin60°=6×=,
∴S△DOE=
S△COD=
S△BOC=BO·CG=×6×=,
∵∠BCD+∠CBO=180°,∴CD∥BE,
∵CG⊥BE,QH⊥BE,
∴QH=CG=,
∴S△BEQ=BE·QH=×12×=,
∵正六边形ABCDEF是以直线BE为对称轴的轴对称图形,矩形PBQE关于点O成中心对称,
∴===.
19.
【答案】
⑴
证明:延长交于点
∵,
∴四边形是平行四边形
∴,为的中点,,∴.
⑵
由⑴得是的中位线
故
又∵,四边形是平行四边形
∴
又∵
∴在中利用勾股定理得
∴.
⑶
可将四边形的面积分为两部分,梯形和三角形,在中利用勾股定理得,由是的中位线得,四边形是平行四边形得,,
∴梯形面积为:;
由和可证得三角形是直角三角形,
其面积为:,
∴四边形的面积为.
八年级数学
第18章
平行四边形
综合训练
一、选择题
1.
矩形具有而平行四边形不具有的性质为(
)
A.对角线相等
B.对角相等
C.对角线互相平分
D.对边相等
2.
如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A.
1 B.
2 C.
3 D.
4
3.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
4.
(2020·襄阳)已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是(
)
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
5.
(2020·贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是( )
A.5
B.20
C.24
D.32
6.
(2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72
B.24
C.48
D.96
7.
(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
8.
(3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
二、填空题
9.
如图,在平行四边中,,则
.
10.
已知正方形的边长是正方形的对角线,则
11.
如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是________.
12.
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
13.
如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
14.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=________度.
15.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于________.
16.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
三、解答题
17.
如图,将?ABCD的边AB延长至点E,使BE=AB,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
18.
(2020·通辽)中心为O的正六边形ABCDEF的半轻为6cm,点P,Q同时分别从A,
D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间
为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
19.
如图,为平行四边形,,,交的延长线于点,交于点.
⑴
求证:;
⑵
若,,,求的长;
⑶
在⑵的条件下,求四边形的面积.
人教版
八年级数学
第18章
平行四边形
综合训练-答案
一、选择题
1.
【答案】A
2.
【答案】C
3.
【答案】C
4.
【答案】B
5.
【答案】
B.
6.
【答案】
C
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
7.
【答案】B
8.
【答案】B
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
二、填空题
9.
【答案】
10.
【答案】
11.
【答案】24 解图
12.
【答案】110°
13.
【答案】21°
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
14.
【答案】15 解图
15.
【答案】
16.
【答案】
三、解答题
17.
【答案】
证明:(1)在?ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵BE=AB,∴BE=DC,
∴四边形BECD是平行四边形,
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知四边形BECD是平行四边形,
则OD=OE,OC=OB.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴BC=ED,
∴平行四边形BECD是矩形.
18.
【答案】
证明:(1)在正六边形ABCDEF中,AB=AF=FE=ED=DC=BC=6,∠A=∠F=∠D=∠C=120°,
∵VP=VQ=1cm/s,∴AP=DQ=t,
∵PF=AF-AP=6-t,CQ=CD-DQ=6-t,
∴PF=CQ=6-t,
在△ABP和△DQE中,
AP=DQ=t,∠A
=∠D
=120°,AB=DE=6,
∴△ABP≌△DQE,∴BP=EQ,
同理可证△PEF≌△QBC,∴PE=QB,
∴四边形PBQE为平行四边形.
(2)连结BE,CO,DO,作CG⊥BE于点G,QH⊥BE于点H.
∵四边形PBQE是矩形,∴∠BQE=90°,
∴BE是正六边形ABCDEF的外接圆直径,
即BE过点O,且BE=12,
∵ED=DC=BC=6,
∴∠EOD=∠COD=∠BOC
=60°,
又∵OE=OD=OC=OB,
∴△EOD,△COD,△BOC是全等的等边三角形,
∴CG=CO·sin∠BOC=CO·sin60°=6×=,
∴S△DOE=
S△COD=
S△BOC=BO·CG=×6×=,
∵∠BCD+∠CBO=180°,∴CD∥BE,
∵CG⊥BE,QH⊥BE,
∴QH=CG=,
∴S△BEQ=BE·QH=×12×=,
∵正六边形ABCDEF是以直线BE为对称轴的轴对称图形,矩形PBQE关于点O成中心对称,
∴===.
19.
【答案】
⑴
证明:延长交于点
∵,
∴四边形是平行四边形
∴,为的中点,,∴.
⑵
由⑴得是的中位线
故
又∵,四边形是平行四边形
∴
又∵
∴在中利用勾股定理得
∴.
⑶
可将四边形的面积分为两部分,梯形和三角形,在中利用勾股定理得,由是的中位线得,四边形是平行四边形得,,
∴梯形面积为:;
由和可证得三角形是直角三角形,
其面积为:,
∴四边形的面积为.
