人教版九年级数学上册24.2.2直线和圆的位置关系学案 (word版 无答案)
文档属性
| 名称 | 人教版九年级数学上册24.2.2直线和圆的位置关系学案 (word版 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 90.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 14:59:53 | ||
图片预览

文档简介
九年级数学导学案
课题:24.2.2直线和圆的位置关系(2)
NO.
主备人:
备课时间:
学科领导签字:
知识点
关键点
易错点
学习目标:1.
理解切线的判定定理和性质,会准确过圆上一点画圆的切线;
2.
经历探索切线判定方法的过程,学会用圆的判定定理进行简单的证明的方法.
3.
养成严谨的学习态度。
重
点:切线的判定和性质
难点预设:应用切线的判定定理解题
一、我学习
我收获
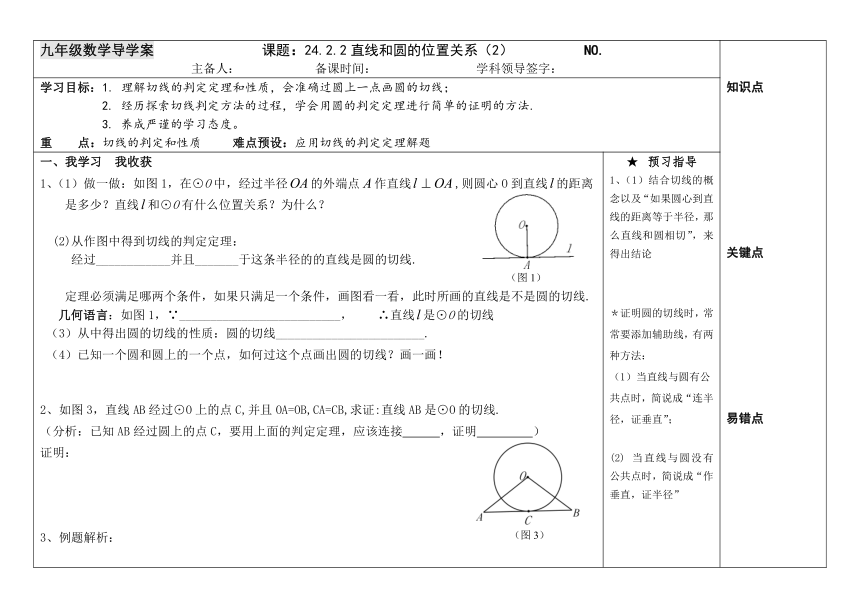
1、(1)做一做:如图1,在⊙O中,经过半径的外端点作直线,则圆心O到直线的距离是多少?直线和⊙O有什么位置关系?为什么?
(2)从作图中得到切线的判定定理:
经过____________并且_______于这条半径的的直线是圆的切线.
定理必须满足哪两个条件,如果只满足一个条件,画图看一看,此时所画的直线是不是圆的切线.
几何语言:如图1,∵__________________________,
∴直线是⊙O的切线
(3)从中得出圆的切线的性质:圆的切线________________________.
(4)已知一个圆和圆上的一个点,如何过这个点画出圆的切线?画一画!
2、如图3,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
(分析:已知AB经过圆上的点C,要用上面的判定定理,应该连接
,证明
)
证明:
3、例题解析:
4、总结:切线的判定方法:(1)________________________;(2)_________________________。
(3)_________________________。
切线的性质:__________________________________。
预习指导
1、(1)结合切线的概念以及“如果圆心到直线的距离等于半径,那么直线和圆相切”,来得出结论
*证明圆的切线时,常常要添加辅助线,有两种方法:
(1)当直线与圆有公共点时,简说成“连半径,证垂直”;
(2)
当直线与圆没有公共点时,简说成“作垂直,证半径”
二、我展示
我精彩(没有完美的个人,只有完美的团队。)
【合作交流】
切线的判定方法的探究
【精讲预设】
切线判定的应用(规律方法总结)
我存在的问题:
预习疑问:
课后疑问:
规律、方法总结
流程安排:
流程一:自主学习(3′)流程二:合作交流(2′)流程三:汇报展示(27′)
流程四:总结升华(3′)流程五:课堂反馈(10′)
三、我检测
我进步
1、下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线.B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
2、已知:如图5,是⊙O外一点,的延长线交⊙O于点,点
在圆上,且,.求证:直线是⊙O的切线.
3、已知:如图4,P是∠AOB的角平分线OC上一点.PE⊥OA于E.以P点为圆心,PE长为半径作⊙P.
求证:⊙P与OB相切.
思路引领
2、直线与圆有公共点,
“连半径,证垂直”;
3、直线与圆没有公共点,
“作垂直,证半径”
四、小结(反思提升)
课题:24.2.2直线和圆的位置关系(2)
NO.
主备人:
备课时间:
学科领导签字:
知识点
关键点
易错点
学习目标:1.
理解切线的判定定理和性质,会准确过圆上一点画圆的切线;
2.
经历探索切线判定方法的过程,学会用圆的判定定理进行简单的证明的方法.
3.
养成严谨的学习态度。
重
点:切线的判定和性质
难点预设:应用切线的判定定理解题
一、我学习
我收获
1、(1)做一做:如图1,在⊙O中,经过半径的外端点作直线,则圆心O到直线的距离是多少?直线和⊙O有什么位置关系?为什么?
(2)从作图中得到切线的判定定理:
经过____________并且_______于这条半径的的直线是圆的切线.
定理必须满足哪两个条件,如果只满足一个条件,画图看一看,此时所画的直线是不是圆的切线.
几何语言:如图1,∵__________________________,
∴直线是⊙O的切线
(3)从中得出圆的切线的性质:圆的切线________________________.
(4)已知一个圆和圆上的一个点,如何过这个点画出圆的切线?画一画!
2、如图3,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
(分析:已知AB经过圆上的点C,要用上面的判定定理,应该连接
,证明
)
证明:
3、例题解析:
4、总结:切线的判定方法:(1)________________________;(2)_________________________。
(3)_________________________。
切线的性质:__________________________________。
预习指导
1、(1)结合切线的概念以及“如果圆心到直线的距离等于半径,那么直线和圆相切”,来得出结论
*证明圆的切线时,常常要添加辅助线,有两种方法:
(1)当直线与圆有公共点时,简说成“连半径,证垂直”;
(2)
当直线与圆没有公共点时,简说成“作垂直,证半径”
二、我展示
我精彩(没有完美的个人,只有完美的团队。)
【合作交流】
切线的判定方法的探究
【精讲预设】
切线判定的应用(规律方法总结)
我存在的问题:
预习疑问:
课后疑问:
规律、方法总结
流程安排:
流程一:自主学习(3′)流程二:合作交流(2′)流程三:汇报展示(27′)
流程四:总结升华(3′)流程五:课堂反馈(10′)
三、我检测
我进步
1、下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线.B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
2、已知:如图5,是⊙O外一点,的延长线交⊙O于点,点
在圆上,且,.求证:直线是⊙O的切线.
3、已知:如图4,P是∠AOB的角平分线OC上一点.PE⊥OA于E.以P点为圆心,PE长为半径作⊙P.
求证:⊙P与OB相切.
思路引领
2、直线与圆有公共点,
“连半径,证垂直”;
3、直线与圆没有公共点,
“作垂直,证半径”
四、小结(反思提升)
同课章节目录
