苏科版八年级上册第3章勾股定理综合练习(word版无答案)
文档属性
| 名称 | 苏科版八年级上册第3章勾股定理综合练习(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 15:28:09 | ||
图片预览

文档简介
勾股定理综合
知识点归纳与总结
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
常见勾股数:3,4,5;?6,8,10;
9,12,15;?5,12,13。?
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。?????
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
二、例题解析与考点突破
例:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7
cm,正方形A、B、C的面积分别是8
cm2、10
cm2、14
cm2,则正方形D的面积是_______cm2.
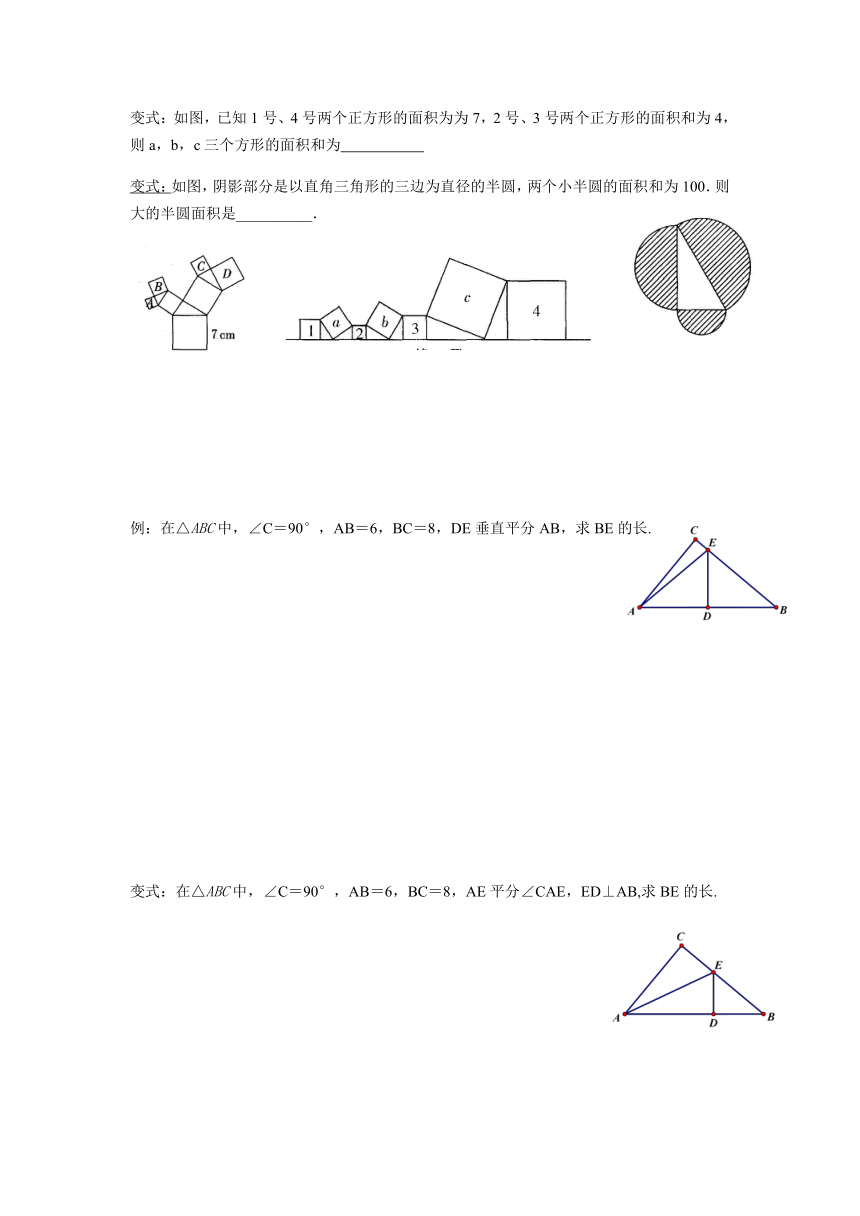
变式:如图,已知1号、4号两个正方形的面积为为7,2号、3号两个正方形的面积和为4,则a,b,c三个方形的面积和为
变式:如图,阴影部分是以直角三角形的三边为直径的半圆,两个小半圆的面积和为100.则大的半圆面积是__________.
例:在△ABC中,∠C=90°,AB=6,BC=8,DE垂直平分AB,求BE的长.
变式:在△ABC中,∠C=90°,AB=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.
变式:如图,折叠长方形纸片ABCD,是点D落在
边BC上的点F处,折痕为AE,AB=CD=6,
AD=BC=10,试求EC的长度.
例:一轮船以16
n
mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12
n
mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距
变式:一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5
m,消防车的云梯最大升长为13
m,则云梯可以达到该建筑物的最大高度是
变式:一棵树在离地面9m处断裂,树的顶部落在离底部12
m处,树折断之前有_______m.
例:如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否回受到噪声的影响?说明理由.如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
变式:如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1
km,BD=3
km,CD=3
km现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20
000元/千米,请你在河CD边上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用?
例:如图5所示,在△中,是边上的高,;在△中,是边上的高,.△的面积是35,求∠的度数.
变式:如图5,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。如果M为CD边的中点,求证:DE:DM:EM=3:4:5。
知识点归纳与总结
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
常见勾股数:3,4,5;?6,8,10;
9,12,15;?5,12,13。?
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。?????
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
二、例题解析与考点突破
例:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7
cm,正方形A、B、C的面积分别是8
cm2、10
cm2、14
cm2,则正方形D的面积是_______cm2.
变式:如图,已知1号、4号两个正方形的面积为为7,2号、3号两个正方形的面积和为4,则a,b,c三个方形的面积和为
变式:如图,阴影部分是以直角三角形的三边为直径的半圆,两个小半圆的面积和为100.则大的半圆面积是__________.
例:在△ABC中,∠C=90°,AB=6,BC=8,DE垂直平分AB,求BE的长.
变式:在△ABC中,∠C=90°,AB=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.
变式:如图,折叠长方形纸片ABCD,是点D落在
边BC上的点F处,折痕为AE,AB=CD=6,
AD=BC=10,试求EC的长度.
例:一轮船以16
n
mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12
n
mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距
变式:一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5
m,消防车的云梯最大升长为13
m,则云梯可以达到该建筑物的最大高度是
变式:一棵树在离地面9m处断裂,树的顶部落在离底部12
m处,树折断之前有_______m.
例:如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否回受到噪声的影响?说明理由.如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
变式:如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1
km,BD=3
km,CD=3
km现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20
000元/千米,请你在河CD边上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用?
例:如图5所示,在△中,是边上的高,;在△中,是边上的高,.△的面积是35,求∠的度数.
变式:如图5,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。如果M为CD边的中点,求证:DE:DM:EM=3:4:5。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
