人教版数学九年级下册第二十七章相似 全章基础同步测试题(word版含答案)
文档属性
| 名称 | 人教版数学九年级下册第二十七章相似 全章基础同步测试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 848.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览


文档简介
27.1图形的相似
一、请认真观察
下面各组中的两个图形,哪些是形状相同的图形,哪些是形状不同的图形.
二、仔细辨认哟!
观察下面图形,指出(1)~(9)中的图形有没有与给出的图形(a)、(b)、(c)形状相同的?
三、请你画一画,试着把下面的两个图形利用给出的格点放大
四、填空
1.放大镜下的图形和原来的图形(
)相似图形,哈哈镜中的图形和原来的图形(
)相似图形(填“是”或“不是”)
2.小颖的妈妈为小颖缝制了一个长50cm,宽30cm的矩形坐垫,又在坐垫的周围缝上一圈宽3cm的花边,妈妈说:“里外两个矩形是相似形”,小颖说:“这两个矩形不是相似形”,你认为谁说得对?并说明你的理由( )
3.如果两个相似多边形的最长边分别为35cm和14cm,那么最短边分别为5cm和( )cm
五、想一想
如图:已知A(0,-2),B(-2,1),C(3,2)
图4—3—1
(1)求线段AB、BC、AC的长.
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求
A′B′、B′C′、A′C′的长.
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
参考答案
一、(3)、(5)组中的图形形状相同
(1)、(2)、(4)、(6)组中的图形形状不同
二、图形(4)、(8)与图形(a)形状相同
图形(6)与图形(b)形状相同
图形(5)与图形(c)形状相同
三、略
四、1.是 不是 2.小颖说的对 3.2cm
五、解:如图(见原题图)A(0,-2),B(-2,1),C(3,2)
(1)由勾股定理得:
AB=
BC=
AC==5
(2)由已知得A′(0,-4),B′(-4,2),C′(6,4)
由勾股定理得:
A′B′=
B′C′=
A′C′==10
(3)∵
∴这六条线段成比例
(4)△ABC与△A′B′C′的形状相同.
人教版
九年级数学
27.2
相似三角形
一、选择题
1.
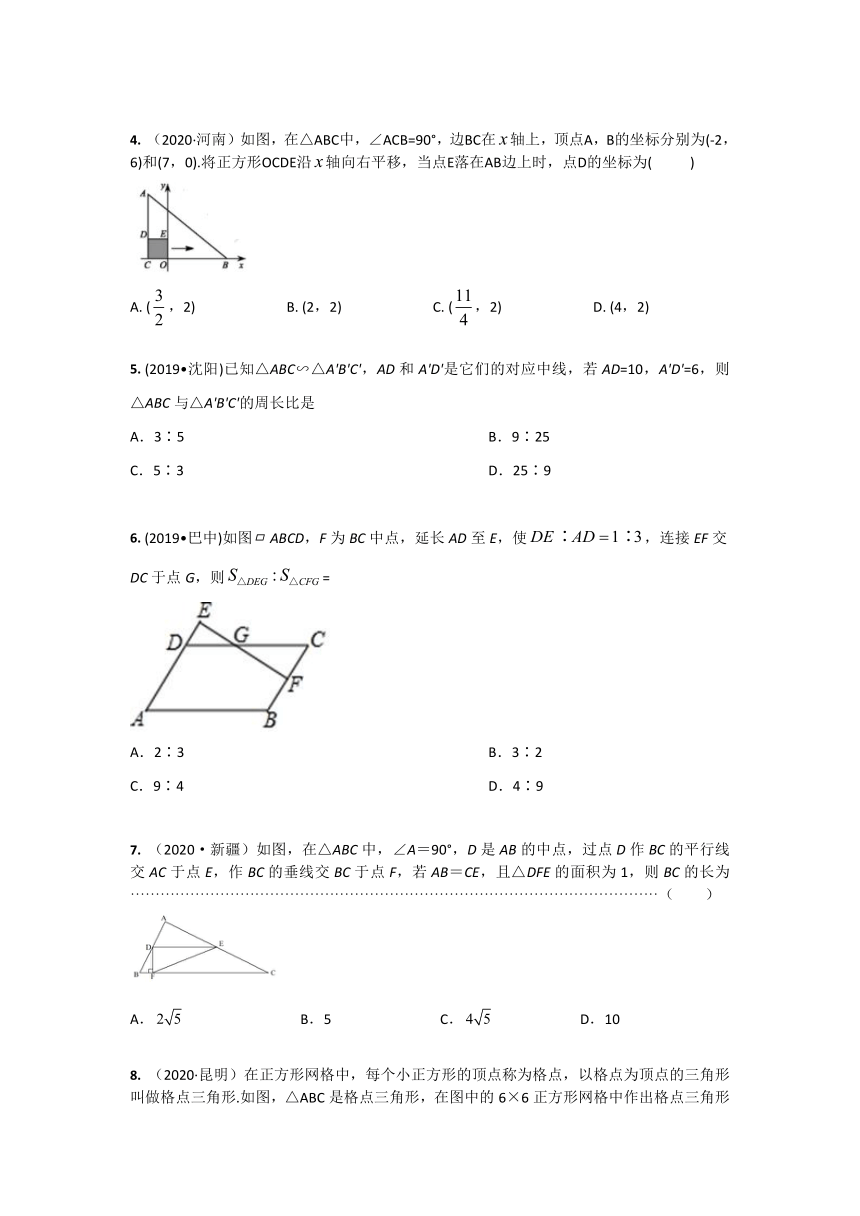
(2020·永州)如图,在中,,四边形的面积为21,则的面积是(
)
A.
B.
25
C.
35
D.
63
2.
(2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
3.
(2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是(
)
A.
B.
C.
D.
4.
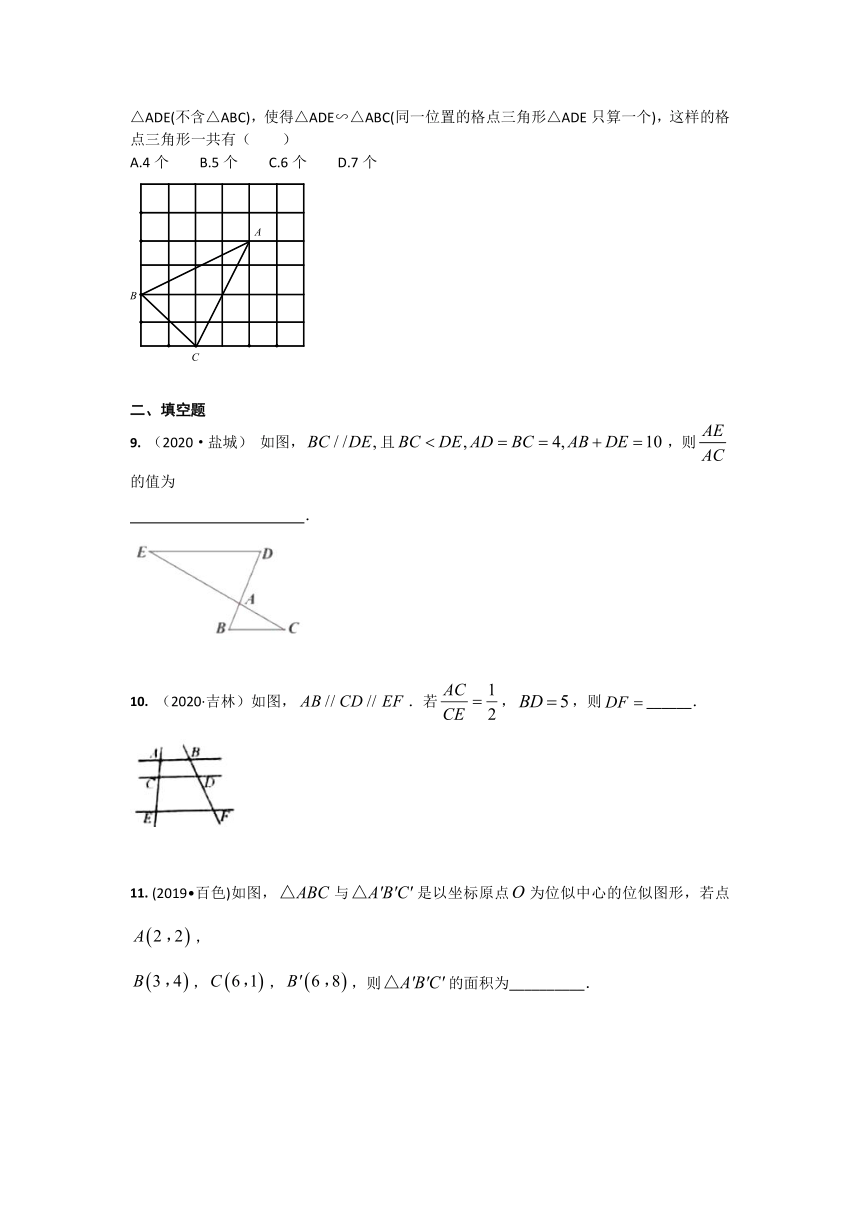
(2020·河南)如图,在△ABC中,∠ACB=90°,边BC在轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿轴向右平移,当点E落在AB边上时,点D的坐标为(
)
A.
(,2)
B.
(2,2)
C.
(,2)
D.
(4,2)
5.
(2019?沈阳)已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是
A.3∶5
B.9∶25
C.5∶3
D.25∶9
6.
(2019?巴中)如图ABCD,F为BC中点,延长AD至E,使,连接EF交DC于点G,则=
A.2∶3
B.3∶2
C.9∶4
D.4∶9
7.
(2020·新疆)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为
( )
A.
B.5
C.
D.10
8.
(2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有(
)
A.4个
B.5个
C.6个
D.7个
二、填空题
9.
(2020·盐城)
如图,且,则的值为
.
10.
(2020·吉林)如图,.若,,则______.
11.
(2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
12.
(2020·东营)如图,P为平行四边形ABCD边BC边上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为、、,若=2,则+=
.
13.
(2020·郴州)在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是
.
14.
(2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
15.
(2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
16.
(2020·杭州)如图是一张矩形纸片,点E在边上,把沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,,则______,______.
三、解答题
17.
(2020·达州)如图,在梯形中,,,,.为线段上的一动点,且和、不重合,连接,过点作交射线于点.
聪聪根据学习函数的经验,对这个问题进行了研究:
(1)通过推理,他发现△ABP∽△PCE,请你帮他完成证明.
(2)利用几何画板,他改变的长度,运动点,得到不同位置时,、的长度的对应值:
当时,得表1:
当时,得表2:
这说明,点在线段上运动时,要保证点总在线段上,的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在和的长度这两个变量中,______的长度为自变量,______的长度为因变量;
②设,当点在线段上运动时,点总在线段上,求的取值范围.
18.
(2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为
cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图①
图
②
图③
人教版
九年级数学
27.2
相似三角形
课时训练-答案
一、选择题
1.
【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
2.
【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
3.
【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
4.
【答案】B
【解析】∵点A,B的坐标分别为(-2,6)和(7,0),∴OC=2,AC=6,OB=7,
∴BC=9,正方形的边长为2.将正方形OCDE沿轴向右平移,当点E落在AB边上时,设正方形与轴的两个交点分别为G、F,∵EF⊥轴,EF=GF=DG=2,∴EF∥AC,D,E两点的纵坐标均为2,
∴,即,解得BF=3.∴OG=OB-BF-GF=7-3-2=2,∴
D点的横坐标为2,∴点D的坐标为
(2,2).
5.
【答案】C
【解析】∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD∶A′D′=10∶6=5∶3.故选C.
6.
【答案】D
【解析】设,∵,∴,
∵四边形ABCD是平行四边形,∴,,
∵点F是BC的中点,∴,
∵,∴,
∴,故选D.
7.
【答案】A
【解析】本题考查了相似三角形的判定与性质,三角形的中位线定理.如答图,过点E作EG⊥BC于G,过点A作AH⊥BC于H.
又因为DF⊥BC,所以DF∥AH∥EG,四边形DEGF是矩形.所以△BDF∽△BAH,DF=EG,所以=,因为D为AB中点,所以=,所以=.设DF=EG=x,则AH=2x.因为∠BAC=90°,所以∠B+∠C=90°,因为EG⊥BC,所以∠C+∠CEG=90°,所以∠B=∠CEG,又因为∠BHA=∠CGE=90°,AB=CE,所以△ABH≌△CEG,所以CG=AH=2x.同理可证△BDF∽△ECG,所以=,因为BD=AB=CE,所以=EG=x.在Rt△BDF中,由勾股定理得BD===x,所以AD=x,所以CE=AB=2AD=x.因为DE∥BC,所以==,所以AE=AC=CE=x.
在Rt△ADE中,由勾股定理得DE===x.因△DEF的面积为1,所以DE·DF=1,即×x·x=1,解得x=,所以DE=×=,因为AD=BD,AE=CE,所以BC=2DE=,因此本题选D.
8.
【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
9.
【答案】2
【解析】∵BC∥DE,∴△ADE∽△ABC,∴
,设DE=x,则AB=10-x∵AD=BC=4,∴,∴x1=8
,x2=2(舍去),
,此本题答案为2
.
10.
【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
11.
【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
12.
【答案】18
【解析】本题考查了相似三角形的判定、性质,三角形的面积,解题的关键是根据已知条件推出相似三角形,并由相似比得到面积比.
∵PA=3PE,PD=3PF,∠APD
=∠EPF,∴△PEF∽△PAD,相似比为1︰3,
∵△PEF的面积为=2,∴=9S=9×2=18,
∴+==18.
13.
【答案】(,2)
【解析】∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是:(×2,×3),即A1(,2).故答案为:(,2).
14.
【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
15.
【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
16.
【答案】2 -1
【解析】设BE=x,则AB=AE+BE=2+x.∵四边形ABCD是矩形,∴CD=AB=2+x,AB∥CD,∴∠DCE=∠BEC.由折叠得∠BEC=∠DEC,EF=BE=x,∴∠DCE=∠DEC.∴DE=CD=2+x.∵点D,F,E在同一条直线上,∴DF=DE-EF=2+x-x=2.∵AB∥CD,∴△DCF∽△EAF,∴=.∴=,解得x1=-1,x2=--1.经检验,x1=-1,x2=--1都是分式方程的根.∵x>0,∴x=-1,即BE=-1.
三、解答题
17.
【答案】
(1)∵AB∥CD,∠B=90°,∴∠C=90°,
∵PE⊥PA,∠B=90°,
∴∠APB+∠EPC=90°,∠APB+∠PAB=90°,∴∠PAB=∠EPC,
在△APB和△EPC中,∠PAB=∠EPC,∠B=∠C=90°,∴△APB∽△EPC.
(2)①BP;CE;
②∵△APB∽△EPC,∴,
∵CD=2,∴CE的最大值为2,,即BP·CP=12,
由表格可知:当BP=2时,CE=2,此时CP=6,BC=BP+CP=8,
∴BC的最大值为8,即0<m<8.
18.
【答案】
解:
(1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
27.3位似
一.选择题
1.在平面直角坐标系中,点A(2,2).B(3,﹣2),△AOB与△A'OB'是以原点O为位似中心的位似图形,且两个三角分别在y轴两侧,相似比为3:2.则点B'的坐标是( )
A.(2,﹣)
B.(,﹣3)
C.(﹣2,)
D.(﹣,3)
2.如图,△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,若A(2,1),则点C的坐标为( )
A.(1,2)
B.(2,1)
C.(2,4)
D.(4,2)
3.如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7)
B.(1,﹣7)
C.(4,﹣4)
D.(1,﹣4)
4.如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,则点A的对应点的坐标是( )
A.(,1)
B.(,﹣1)
C.(8,16)或(﹣16,﹣8)
D.(8,16)或(﹣8,﹣16)
5.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点O为位似中心,把这个三角形放大为原来的2倍,得到△CDO,则点A的对应点C的坐标为( )
A.(﹣4,8)
B.(4,﹣8)
C.(﹣4,8)或(4,﹣8)
D.(﹣1,2)或(1,﹣2)
6.已知△ABC与△A1B1C1是关于原点为中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(4,2)
B.(﹣4,﹣2)
C.(4,2)或(﹣4,﹣2)
D.(6,3)
7.如图,在平面直角坐标系xOy中,△ABC和△A'B'C′位似,位似中心为原点O,点A(﹣1,2)、点A'(2,﹣4),若△ABC的面积为4,则△A'B'C′的面积是( )
A.2
B.4
C.8
D.16
8.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )
A.1:2
B.1:3
C.1:4
D.1:9
9.如图,平面直角坐标系中,点A(﹣2,0),B(0,1),C(﹣3,2),以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,则点C的对应点C′的坐标为( )
A.(﹣1.5,1)
B.(﹣1.5,1)或(1.5,﹣1)
C.(﹣6,4)
D.(﹣6,4)或(6,﹣4)
10.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O
B.点P
C.点M
D.点N
二.填空题
11.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A'B'O.若点A的坐标是(1,2),则点A'的坐标是
.
12.如果两个三角形不仅是相似三角形,而且每组对应点的连线交于一点,那么这两个三角形叫做位似三角形,这个点叫做位似中心.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4.则A1B1的长为
.
13.如图,在平面直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且位似比为2:1,点A、B都在格点上,则点B′的坐标是
.
14.如图,已知矩形ABCD和矩形BEFG是位似图形,点O是位似中心,若点D的坐标为(1,2),点F的坐标为(4,4),则点G的坐标是
.
15.如图,四边形OABC的顶点O为坐标原点,以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,若A(6,0)的对应点为A1(4,0),四边形OABC的面积为27,则四边形OA1B1C1的面积为
.
三.解答题
16.如图,在正方形格中,每一个小正方形的边长都为1,△ABC的顶点分别为A(2,3),B(2,1),C(5,4).
(1)写出△ABC的外心P的坐标
.
(2)以(1)中的外心P为位似中心,按位似比2:1在位似中心的同侧将△ABC放大为△A′B′C′,放大后点A、B、C的对应点分别为A′、B′,C′,请在图中画出△ABC.
17.如图,在平面直角坐标系中.△ABC的三个顶点的坐标分别是A(1,3)、B(4,1)、C(1,1).
(1)在所给网格中画出△ABC以点O为位似中心的位似图形△A1B1C1.且△ABC与△A1B1C1的相似比为1:2.
(2)直线AA1所对应的函数表达式为
.
18.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣1,﹣1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点B2的坐标;
(3)把△ABC以点A为位似中心,在x轴下方放大,使放大前后对应边长的比为1:2,在方格纸中画出△AB3C3的图形.
参考答案
一.选择题
1.解:如图,∵△AOB∽△A′OB′,相似比为3:2,B(3,﹣2),
∴B′(2,),
故选:C.
2.解:∵△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,点A的坐标为(2,1),
∴点C的坐标为(2×2,1×2),即(4,2),
故选:D.
3.解:以C为坐标原点建立平面直角坐标系,则点A在新坐标系中的坐标为(﹣1,3),
∵△ABC与△A'B'C'以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',把△ABC的边长放大为原来的2倍,
∴点A'在新坐标系中的坐标为(1×2,﹣3×2),即(2,﹣6),
则点A'的坐标为(1,﹣7),
故选:B.
4.解:∵点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,
∴点A的对应点的坐标是:(8,16)或(﹣8,﹣16).
故选:D.
5.解:∵△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点为位似中心,将这个三角形放大为原来的2倍,得到△CDO,
∴点A的对应点C的坐标为:(﹣4,8)或(4,﹣8).
故选:C.
6.解:△ABC与△A1B1C1是关于原点为中心的位似图形,A(2,1),
△ABC与△A1B1C1的相似比为,
∴A的对应点A1的坐标是(2×2,1×2)或(﹣2×2,﹣1×2),即(4,2)或(﹣4,﹣2),
故选:C.
7.解:∵△ABC和△A'B'C′位似,位似中心为原点O,点A(﹣1,2)、点A'(2,﹣4),
∴△ABC和△A'B'C′的相似比为:1:2,
∵△ABC的面积为4,
∴△A'B'C′的面积是:16.
故选:D.
8.解:∵点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,OA:OA1=1:3,
∴五边形ABCDE和五边形A1B1C1D1E1的位似比为:1:3,
∴五边形ABCDE和五边形A1B1C1D1E1的面积比是:1:9.
故选:D.
9.解:以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,
∵点C的坐标为(﹣3,2),
∴点C的对应点C′的坐标为(﹣3×,2×)或(3×,﹣2×),即(﹣1.5,1)或(1.5,﹣1),
故选:B.
10.解:如图所示:两个三角形的位似中心是:点P.
故选:B.
二.填空题
11.解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点A的坐标是(1,2),则点A′的坐标是(﹣2,﹣4),
故答案为:(﹣2,﹣4).
12.解:∵△ABC和△A1B1C1是以点O为位似中心的位似三角形,
∴OC1:OC=OA1:OA=1:2,A1B1∥AB,
∴OA1:OA=A1B1:AB=1:2,
∴A1B1=AB=×4=2.
故答案为2.
13.解:△AOB与△A′OB′是以原点O为位似中心的位似图形,位似比为2:1,点B的坐标为(4,﹣4),
∴点B′的坐标为(4×,﹣4×)或(﹣4×,4×),即(2,﹣2)或(﹣2,2),
故答案为:(2,﹣2)或(﹣2,2).
14.解:∵矩形ABCD,点D的坐标为(1,2),
∴AD=BC=2,
∵矩形BEFG,点F的坐标为(4,4),
∴EF=BG=4,
∴===,
∴OB=2,
故点G的坐标是(2,4).
故答案为:(2,4).
15.解:∵以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,A(6,0)的对应点为A1(4,0),
∴四边形OA1B1C1与四边形OABC的位似比为:4:6=2:3,
∴四边形OA1B1C1与四边形OABC的面积比为:4:9,
∵四边形OABC的面积为27,
∴四边形OA1B1C1的面积为:27×=12.
故答案为:12.
三.解答题
16.解:(1)如图.P点坐标为(4,2);
故答案为(4,2);
(2)如图,△A′B′C′为所作.
17.解:(1)如图,△A1B1C1为所作;
(2)设直线AA1的解析式为y=kx+b,
把A(1,3),A1(﹣2,﹣6)代入得,解得,
所以直线AA1的解析式为y=3x.
故答案为y=3x.
18.解:(1)如图,△A1B1C1为所作,点B1的坐标为(﹣9,﹣1);
(2)如图,△A2B2C为所作,点B2的坐标为(5,5);
(3)如图,△AB3C3为所作.
一、请认真观察
下面各组中的两个图形,哪些是形状相同的图形,哪些是形状不同的图形.
二、仔细辨认哟!
观察下面图形,指出(1)~(9)中的图形有没有与给出的图形(a)、(b)、(c)形状相同的?
三、请你画一画,试着把下面的两个图形利用给出的格点放大
四、填空
1.放大镜下的图形和原来的图形(
)相似图形,哈哈镜中的图形和原来的图形(
)相似图形(填“是”或“不是”)
2.小颖的妈妈为小颖缝制了一个长50cm,宽30cm的矩形坐垫,又在坐垫的周围缝上一圈宽3cm的花边,妈妈说:“里外两个矩形是相似形”,小颖说:“这两个矩形不是相似形”,你认为谁说得对?并说明你的理由( )
3.如果两个相似多边形的最长边分别为35cm和14cm,那么最短边分别为5cm和( )cm
五、想一想
如图:已知A(0,-2),B(-2,1),C(3,2)
图4—3—1
(1)求线段AB、BC、AC的长.
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求
A′B′、B′C′、A′C′的长.
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
参考答案
一、(3)、(5)组中的图形形状相同
(1)、(2)、(4)、(6)组中的图形形状不同
二、图形(4)、(8)与图形(a)形状相同
图形(6)与图形(b)形状相同
图形(5)与图形(c)形状相同
三、略
四、1.是 不是 2.小颖说的对 3.2cm
五、解:如图(见原题图)A(0,-2),B(-2,1),C(3,2)
(1)由勾股定理得:
AB=
BC=
AC==5
(2)由已知得A′(0,-4),B′(-4,2),C′(6,4)
由勾股定理得:
A′B′=
B′C′=
A′C′==10
(3)∵
∴这六条线段成比例
(4)△ABC与△A′B′C′的形状相同.
人教版
九年级数学
27.2
相似三角形
一、选择题
1.
(2020·永州)如图,在中,,四边形的面积为21,则的面积是(
)
A.
B.
25
C.
35
D.
63
2.
(2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
3.
(2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是(
)
A.
B.
C.
D.
4.
(2020·河南)如图,在△ABC中,∠ACB=90°,边BC在轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿轴向右平移,当点E落在AB边上时,点D的坐标为(
)
A.
(,2)
B.
(2,2)
C.
(,2)
D.
(4,2)
5.
(2019?沈阳)已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是
A.3∶5
B.9∶25
C.5∶3
D.25∶9
6.
(2019?巴中)如图ABCD,F为BC中点,延长AD至E,使,连接EF交DC于点G,则=
A.2∶3
B.3∶2
C.9∶4
D.4∶9
7.
(2020·新疆)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为
( )
A.
B.5
C.
D.10
8.
(2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有(
)
A.4个
B.5个
C.6个
D.7个
二、填空题
9.
(2020·盐城)
如图,且,则的值为
.
10.
(2020·吉林)如图,.若,,则______.
11.
(2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
12.
(2020·东营)如图,P为平行四边形ABCD边BC边上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为、、,若=2,则+=
.
13.
(2020·郴州)在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是
.
14.
(2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
15.
(2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
16.
(2020·杭州)如图是一张矩形纸片,点E在边上,把沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,,则______,______.
三、解答题
17.
(2020·达州)如图,在梯形中,,,,.为线段上的一动点,且和、不重合,连接,过点作交射线于点.
聪聪根据学习函数的经验,对这个问题进行了研究:
(1)通过推理,他发现△ABP∽△PCE,请你帮他完成证明.
(2)利用几何画板,他改变的长度,运动点,得到不同位置时,、的长度的对应值:
当时,得表1:
当时,得表2:
这说明,点在线段上运动时,要保证点总在线段上,的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在和的长度这两个变量中,______的长度为自变量,______的长度为因变量;
②设,当点在线段上运动时,点总在线段上,求的取值范围.
18.
(2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为
cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图①
图
②
图③
人教版
九年级数学
27.2
相似三角形
课时训练-答案
一、选择题
1.
【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
2.
【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
3.
【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
4.
【答案】B
【解析】∵点A,B的坐标分别为(-2,6)和(7,0),∴OC=2,AC=6,OB=7,
∴BC=9,正方形的边长为2.将正方形OCDE沿轴向右平移,当点E落在AB边上时,设正方形与轴的两个交点分别为G、F,∵EF⊥轴,EF=GF=DG=2,∴EF∥AC,D,E两点的纵坐标均为2,
∴,即,解得BF=3.∴OG=OB-BF-GF=7-3-2=2,∴
D点的横坐标为2,∴点D的坐标为
(2,2).
5.
【答案】C
【解析】∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD∶A′D′=10∶6=5∶3.故选C.
6.
【答案】D
【解析】设,∵,∴,
∵四边形ABCD是平行四边形,∴,,
∵点F是BC的中点,∴,
∵,∴,
∴,故选D.
7.
【答案】A
【解析】本题考查了相似三角形的判定与性质,三角形的中位线定理.如答图,过点E作EG⊥BC于G,过点A作AH⊥BC于H.
又因为DF⊥BC,所以DF∥AH∥EG,四边形DEGF是矩形.所以△BDF∽△BAH,DF=EG,所以=,因为D为AB中点,所以=,所以=.设DF=EG=x,则AH=2x.因为∠BAC=90°,所以∠B+∠C=90°,因为EG⊥BC,所以∠C+∠CEG=90°,所以∠B=∠CEG,又因为∠BHA=∠CGE=90°,AB=CE,所以△ABH≌△CEG,所以CG=AH=2x.同理可证△BDF∽△ECG,所以=,因为BD=AB=CE,所以=EG=x.在Rt△BDF中,由勾股定理得BD===x,所以AD=x,所以CE=AB=2AD=x.因为DE∥BC,所以==,所以AE=AC=CE=x.
在Rt△ADE中,由勾股定理得DE===x.因△DEF的面积为1,所以DE·DF=1,即×x·x=1,解得x=,所以DE=×=,因为AD=BD,AE=CE,所以BC=2DE=,因此本题选D.
8.
【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
9.
【答案】2
【解析】∵BC∥DE,∴△ADE∽△ABC,∴
,设DE=x,则AB=10-x∵AD=BC=4,∴,∴x1=8
,x2=2(舍去),
,此本题答案为2
.
10.
【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
11.
【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
12.
【答案】18
【解析】本题考查了相似三角形的判定、性质,三角形的面积,解题的关键是根据已知条件推出相似三角形,并由相似比得到面积比.
∵PA=3PE,PD=3PF,∠APD
=∠EPF,∴△PEF∽△PAD,相似比为1︰3,
∵△PEF的面积为=2,∴=9S=9×2=18,
∴+==18.
13.
【答案】(,2)
【解析】∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是:(×2,×3),即A1(,2).故答案为:(,2).
14.
【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
15.
【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
16.
【答案】2 -1
【解析】设BE=x,则AB=AE+BE=2+x.∵四边形ABCD是矩形,∴CD=AB=2+x,AB∥CD,∴∠DCE=∠BEC.由折叠得∠BEC=∠DEC,EF=BE=x,∴∠DCE=∠DEC.∴DE=CD=2+x.∵点D,F,E在同一条直线上,∴DF=DE-EF=2+x-x=2.∵AB∥CD,∴△DCF∽△EAF,∴=.∴=,解得x1=-1,x2=--1.经检验,x1=-1,x2=--1都是分式方程的根.∵x>0,∴x=-1,即BE=-1.
三、解答题
17.
【答案】
(1)∵AB∥CD,∠B=90°,∴∠C=90°,
∵PE⊥PA,∠B=90°,
∴∠APB+∠EPC=90°,∠APB+∠PAB=90°,∴∠PAB=∠EPC,
在△APB和△EPC中,∠PAB=∠EPC,∠B=∠C=90°,∴△APB∽△EPC.
(2)①BP;CE;
②∵△APB∽△EPC,∴,
∵CD=2,∴CE的最大值为2,,即BP·CP=12,
由表格可知:当BP=2时,CE=2,此时CP=6,BC=BP+CP=8,
∴BC的最大值为8,即0<m<8.
18.
【答案】
解:
(1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
27.3位似
一.选择题
1.在平面直角坐标系中,点A(2,2).B(3,﹣2),△AOB与△A'OB'是以原点O为位似中心的位似图形,且两个三角分别在y轴两侧,相似比为3:2.则点B'的坐标是( )
A.(2,﹣)
B.(,﹣3)
C.(﹣2,)
D.(﹣,3)
2.如图,△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,若A(2,1),则点C的坐标为( )
A.(1,2)
B.(2,1)
C.(2,4)
D.(4,2)
3.如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7)
B.(1,﹣7)
C.(4,﹣4)
D.(1,﹣4)
4.如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,则点A的对应点的坐标是( )
A.(,1)
B.(,﹣1)
C.(8,16)或(﹣16,﹣8)
D.(8,16)或(﹣8,﹣16)
5.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点O为位似中心,把这个三角形放大为原来的2倍,得到△CDO,则点A的对应点C的坐标为( )
A.(﹣4,8)
B.(4,﹣8)
C.(﹣4,8)或(4,﹣8)
D.(﹣1,2)或(1,﹣2)
6.已知△ABC与△A1B1C1是关于原点为中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(4,2)
B.(﹣4,﹣2)
C.(4,2)或(﹣4,﹣2)
D.(6,3)
7.如图,在平面直角坐标系xOy中,△ABC和△A'B'C′位似,位似中心为原点O,点A(﹣1,2)、点A'(2,﹣4),若△ABC的面积为4,则△A'B'C′的面积是( )
A.2
B.4
C.8
D.16
8.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )
A.1:2
B.1:3
C.1:4
D.1:9
9.如图,平面直角坐标系中,点A(﹣2,0),B(0,1),C(﹣3,2),以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,则点C的对应点C′的坐标为( )
A.(﹣1.5,1)
B.(﹣1.5,1)或(1.5,﹣1)
C.(﹣6,4)
D.(﹣6,4)或(6,﹣4)
10.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O
B.点P
C.点M
D.点N
二.填空题
11.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A'B'O.若点A的坐标是(1,2),则点A'的坐标是
.
12.如果两个三角形不仅是相似三角形,而且每组对应点的连线交于一点,那么这两个三角形叫做位似三角形,这个点叫做位似中心.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4.则A1B1的长为
.
13.如图,在平面直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且位似比为2:1,点A、B都在格点上,则点B′的坐标是
.
14.如图,已知矩形ABCD和矩形BEFG是位似图形,点O是位似中心,若点D的坐标为(1,2),点F的坐标为(4,4),则点G的坐标是
.
15.如图,四边形OABC的顶点O为坐标原点,以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,若A(6,0)的对应点为A1(4,0),四边形OABC的面积为27,则四边形OA1B1C1的面积为
.
三.解答题
16.如图,在正方形格中,每一个小正方形的边长都为1,△ABC的顶点分别为A(2,3),B(2,1),C(5,4).
(1)写出△ABC的外心P的坐标
.
(2)以(1)中的外心P为位似中心,按位似比2:1在位似中心的同侧将△ABC放大为△A′B′C′,放大后点A、B、C的对应点分别为A′、B′,C′,请在图中画出△ABC.
17.如图,在平面直角坐标系中.△ABC的三个顶点的坐标分别是A(1,3)、B(4,1)、C(1,1).
(1)在所给网格中画出△ABC以点O为位似中心的位似图形△A1B1C1.且△ABC与△A1B1C1的相似比为1:2.
(2)直线AA1所对应的函数表达式为
.
18.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣1,﹣1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点B2的坐标;
(3)把△ABC以点A为位似中心,在x轴下方放大,使放大前后对应边长的比为1:2,在方格纸中画出△AB3C3的图形.
参考答案
一.选择题
1.解:如图,∵△AOB∽△A′OB′,相似比为3:2,B(3,﹣2),
∴B′(2,),
故选:C.
2.解:∵△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,点A的坐标为(2,1),
∴点C的坐标为(2×2,1×2),即(4,2),
故选:D.
3.解:以C为坐标原点建立平面直角坐标系,则点A在新坐标系中的坐标为(﹣1,3),
∵△ABC与△A'B'C'以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',把△ABC的边长放大为原来的2倍,
∴点A'在新坐标系中的坐标为(1×2,﹣3×2),即(2,﹣6),
则点A'的坐标为(1,﹣7),
故选:B.
4.解:∵点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,
∴点A的对应点的坐标是:(8,16)或(﹣8,﹣16).
故选:D.
5.解:∵△ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点为位似中心,将这个三角形放大为原来的2倍,得到△CDO,
∴点A的对应点C的坐标为:(﹣4,8)或(4,﹣8).
故选:C.
6.解:△ABC与△A1B1C1是关于原点为中心的位似图形,A(2,1),
△ABC与△A1B1C1的相似比为,
∴A的对应点A1的坐标是(2×2,1×2)或(﹣2×2,﹣1×2),即(4,2)或(﹣4,﹣2),
故选:C.
7.解:∵△ABC和△A'B'C′位似,位似中心为原点O,点A(﹣1,2)、点A'(2,﹣4),
∴△ABC和△A'B'C′的相似比为:1:2,
∵△ABC的面积为4,
∴△A'B'C′的面积是:16.
故选:D.
8.解:∵点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,OA:OA1=1:3,
∴五边形ABCDE和五边形A1B1C1D1E1的位似比为:1:3,
∴五边形ABCDE和五边形A1B1C1D1E1的面积比是:1:9.
故选:D.
9.解:以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,
∵点C的坐标为(﹣3,2),
∴点C的对应点C′的坐标为(﹣3×,2×)或(3×,﹣2×),即(﹣1.5,1)或(1.5,﹣1),
故选:B.
10.解:如图所示:两个三角形的位似中心是:点P.
故选:B.
二.填空题
11.解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点A的坐标是(1,2),则点A′的坐标是(﹣2,﹣4),
故答案为:(﹣2,﹣4).
12.解:∵△ABC和△A1B1C1是以点O为位似中心的位似三角形,
∴OC1:OC=OA1:OA=1:2,A1B1∥AB,
∴OA1:OA=A1B1:AB=1:2,
∴A1B1=AB=×4=2.
故答案为2.
13.解:△AOB与△A′OB′是以原点O为位似中心的位似图形,位似比为2:1,点B的坐标为(4,﹣4),
∴点B′的坐标为(4×,﹣4×)或(﹣4×,4×),即(2,﹣2)或(﹣2,2),
故答案为:(2,﹣2)或(﹣2,2).
14.解:∵矩形ABCD,点D的坐标为(1,2),
∴AD=BC=2,
∵矩形BEFG,点F的坐标为(4,4),
∴EF=BG=4,
∴===,
∴OB=2,
故点G的坐标是(2,4).
故答案为:(2,4).
15.解:∵以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,A(6,0)的对应点为A1(4,0),
∴四边形OA1B1C1与四边形OABC的位似比为:4:6=2:3,
∴四边形OA1B1C1与四边形OABC的面积比为:4:9,
∵四边形OABC的面积为27,
∴四边形OA1B1C1的面积为:27×=12.
故答案为:12.
三.解答题
16.解:(1)如图.P点坐标为(4,2);
故答案为(4,2);
(2)如图,△A′B′C′为所作.
17.解:(1)如图,△A1B1C1为所作;
(2)设直线AA1的解析式为y=kx+b,
把A(1,3),A1(﹣2,﹣6)代入得,解得,
所以直线AA1的解析式为y=3x.
故答案为y=3x.
18.解:(1)如图,△A1B1C1为所作,点B1的坐标为(﹣9,﹣1);
(2)如图,△A2B2C为所作,点B2的坐标为(5,5);
(3)如图,△AB3C3为所作.
