2020-2021学年八年级第一学期数学(沪教版)期末复习卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级第一学期数学(沪教版)期末复习卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 191.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览

文档简介
2020-2021学年第一学期八年级数学(沪教版)期末复习卷
一、单选题(共10题;共30分)
1.在函数
中,自变量x
的取值范围为( )
A.???????????????????????B.???????????????????????C.?
且
??????????????????????D.?
且
2.下列计算正确的是(?
)
A.???????????B.???????????C.???????????D.?
3.下列等式中,一定是一元二次方程的是(
??)
A.?
?????????????????B.??????????????????C.?
?????????????????D.?
(
,
为常数)
4.一元二次方程
的一次项系数是(?????
)
A.?-2??????????????????????????????????????????B.?2??????????????????????????????????????????C.?-3??????????????????????????????????????????D.?3
5.如果关于x的一元二次方程ax2+x-1=0有两个不相等的实数根,则a的取值范围是(?????
)
A.?a>-
????????????????????????B.?a≥-
????????????????????????C.?a≥-
且a≠0????????????????????????D.?a>-
且a≠0
6.已知关于
的方程
有实数根,则
的取值范围是
(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
且
7.关于x的一元二次方程x2+bx﹣1=0的判别式为(??
)
A.?1﹣b2??????????????????????????????????B.?b2﹣4??????????????????????????????????C.?b2+4??????????????????????????????????D.?b2+1
8.小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )
A.?????????????????B.?????????????????C.?????????????????D.?
9.已知正比例函数
,且y随x的增大而减少,则直线
的图像是(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
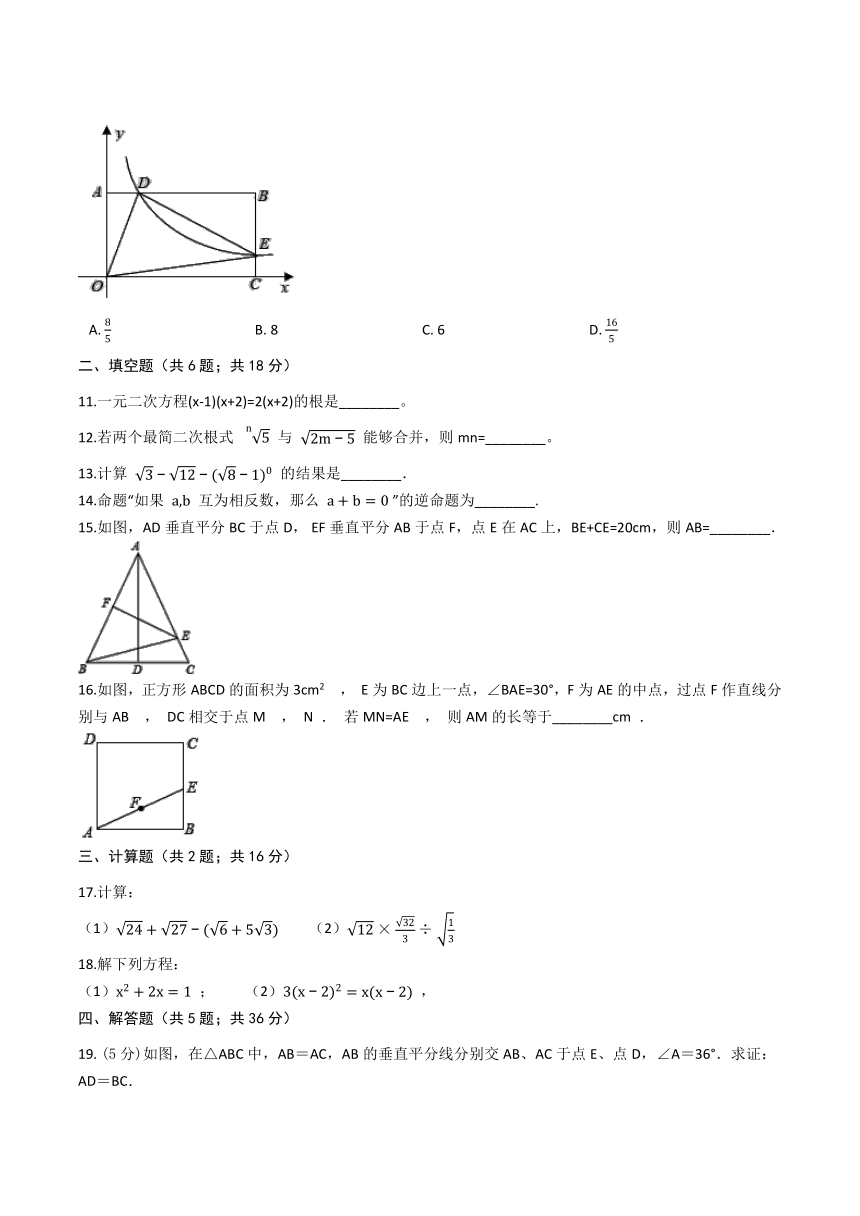
10.如图,在以
为原点的平面直角坐标系中,矩形
的两边
、
分别在
轴、
轴的正半轴上,反比例函数
的图象与
相交于点
,与
相交于点
,若
,且
的面积是
,则
的值为(??
).
A.???????????????????????????????????????????B.?8??????????????????????????????????????????C.?6??????????????????????????????????????????D.?
二、填空题(共6题;共18分)
11.一元二次方程(x-1)(x+2)=2(x+2)的根是________。
12.若两个最简二次根式
与
能够合并,则mn=________。
13.计算
的结果是________.
14.命题“如果
互为相反数,那么
”的逆命题为________.
15.如图,AD垂直平分BC于点D,?EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB=________.
16.如图,正方形ABCD的面积为3cm2
,
E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB
,
DC相交于点M
,
N
.
若MN=AE
,
则AM的长等于________cm
.
三、计算题(共2题;共16分)
17.计算:
(1)
(2)
18.解下列方程:
(1)
;
(2)
,
四、解答题(共5题;共36分)
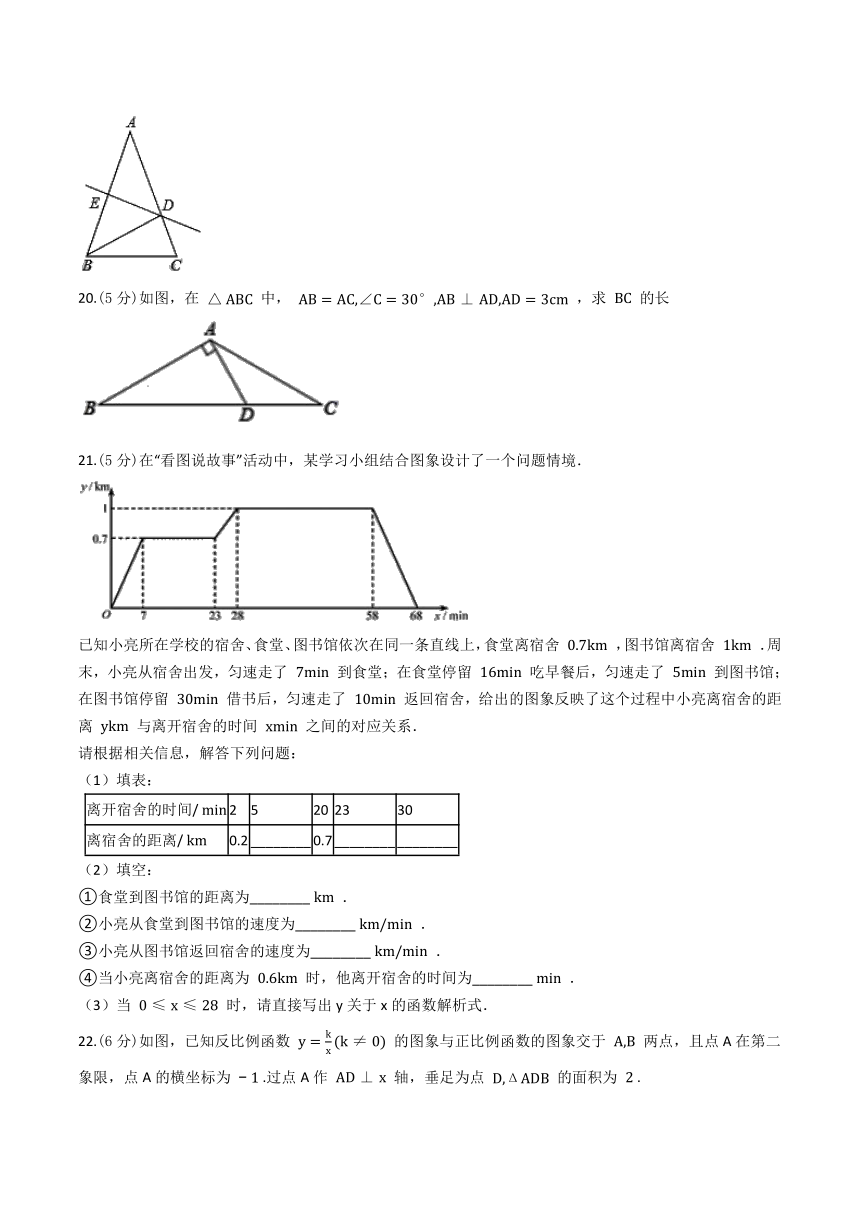
19.(5分)如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、AC于点E、点D,∠A=36°.求证:AD=BC.
20.(5分)如图,在
中,
,求
的长
21.(5分)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍
,图书馆离宿舍
.周末,小亮从宿舍出发,匀速走了
到食堂;在食堂停留
吃早餐后,匀速走了
到图书馆;在图书馆停留
借书后,匀速走了
返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离
与离开宿舍的时间
之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
________
0.7
________
________
(2)填空:
①食堂到图书馆的距离为________
.
②小亮从食堂到图书馆的速度为________
.
③小亮从图书馆返回宿舍的速度为________
.
④当小亮离宿舍的距离为
时,他离开宿舍的时间为________
.
(3)当
时,请直接写出y关于x的函数解析式.
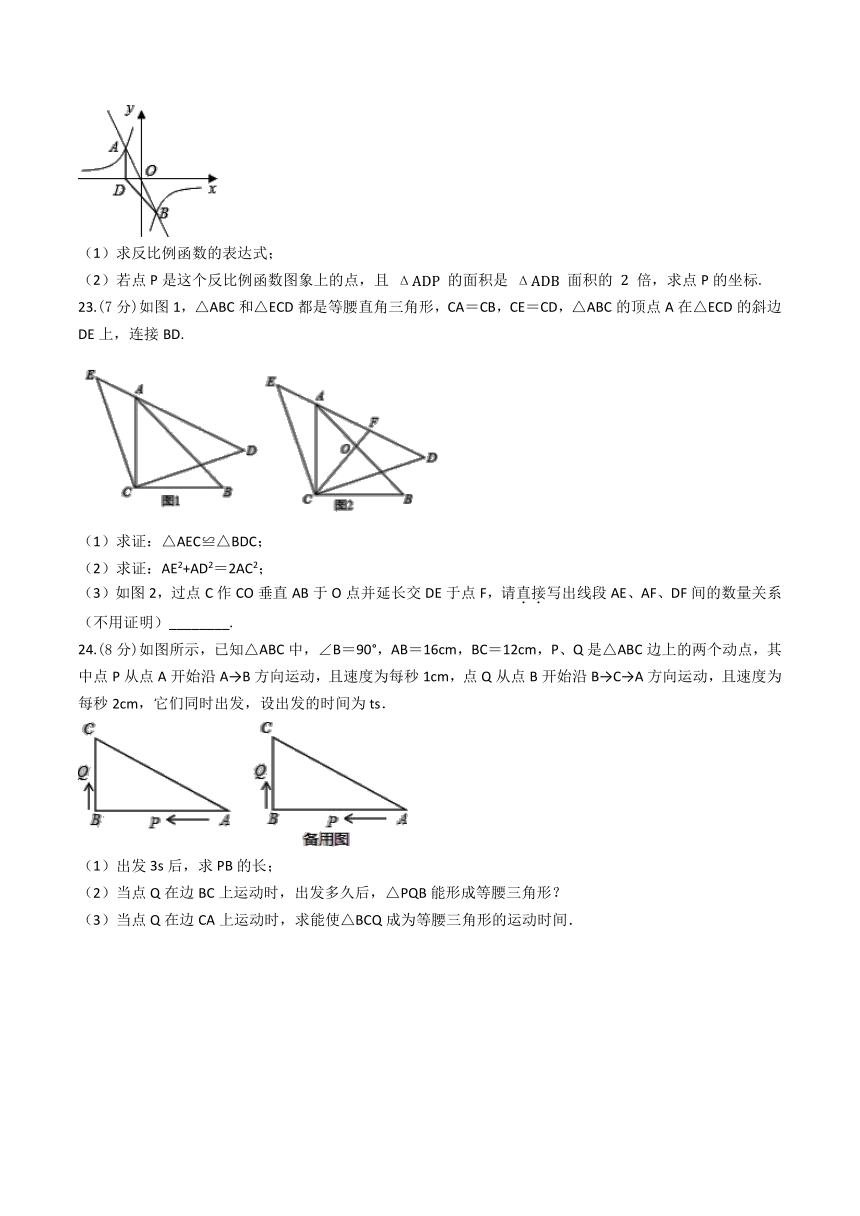
22.(6分)如图,已知反比例函数
的图象与正比例函数的图象交于
两点,且点A在第二象限,点A的横坐标为
.过点A作
轴,垂足为点
的面积为
.
(1)求反比例函数的表达式;
(2)若点P是这个反比例函数图象上的点,且
的面积是
面积的
倍,求点P的坐标.
23.(7分)如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上,连接BD.
(1)求证:△AEC≌△BDC;
(2)求证:AE2+AD2=2AC2;
(3)如图2,过点C作CO垂直AB于O点并延长交DE于点F,请直接写出线段AE、AF、DF间的数量关系(不用证明)________.
24.(8分)如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1)出发3s后,求PB的长;
(2)当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
参考答案
单选题
1
2
3
4
5
6
7
8
9
10
C
C
A
A
D
C
C
C
D
D
二、填空题
11.
x1=-2,x2=3
12.
10
13.
14.
如果
,那么
互为相反数
15.
20cm
16.
或
三、计算题
17.
(1)解:原式
.
(2)解:原式
.
18.
(1)解:
,
,
,
,
,
即
;
(2)解:
,
,
,即
,
或
,
或
,
即
.
四、解答题
19.
证明:∵AB的垂直平分线分别交AB、AC于点E、点D,
∴DB=DA,
∴△ABD是等腰三角形;
∵∠A=36°,
∴∠ABD=∠A=36°,∠ABC=∠C=(180°﹣36°)÷2=72°,
∴∠BDC=∠A+∠ABD=72°,
∴∠C=∠BDC,
∴BD=BC,
∴AD=BC.
20.
解:
,
,
,
在
中,
,
,
,
,
,
,
即BC的长为
.
21.
(1)0.5;0.7;1
(2)0.3;0.06;0.1;6或62
(3)解:当
时,
;
当
时,
当
时,设
,将(23,0.7)(28,1)代入解析式
,解得
∴
.
22.
(1)解:
反比例函数
的图象与正比例函数的图象交于A,B两点,
点A与点B关于原点对称,
,
,
,
而
,
,
反比例函数解析式为
;
(2)解:把
代入
得
,
点坐标为
,
设正比例函数解析式为
,
把
代入得
,
正比例函数解析式为
;
设P点坐标为
,
点坐标为
,
,
的面积是
面积的2倍,即
的面积为4,
,解得
或
,
当
时,
,此时P点坐标为
;
当
时,
,此时P点坐标为
,
综上所述,点P坐标为
或
.
23.
(1)证明:连接
,
,
,
在
和
中,
,
;
(2)证明:
,
,
,
又
,
.
在
中,由勾股定理可知
,
同理,在
中,
,
又
,
,
.
(3)
24.
(1)解:当t=3时,则AP=3,
∵AB=16cm,
∴PB=AB﹣AP=16﹣3=13(cm)
(2)解:由题意可知AP=t,BQ=2t,
∵AB=16,
∴BP=AB﹣AP=16﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即16﹣t=2t,解得t=
,
∴出发
秒后△PQB能形成等腰三角形;
(3)解:①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则
,
∴
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
一、单选题(共10题;共30分)
1.在函数
中,自变量x
的取值范围为( )
A.???????????????????????B.???????????????????????C.?
且
??????????????????????D.?
且
2.下列计算正确的是(?
)
A.???????????B.???????????C.???????????D.?
3.下列等式中,一定是一元二次方程的是(
??)
A.?
?????????????????B.??????????????????C.?
?????????????????D.?
(
,
为常数)
4.一元二次方程
的一次项系数是(?????
)
A.?-2??????????????????????????????????????????B.?2??????????????????????????????????????????C.?-3??????????????????????????????????????????D.?3
5.如果关于x的一元二次方程ax2+x-1=0有两个不相等的实数根,则a的取值范围是(?????
)
A.?a>-
????????????????????????B.?a≥-
????????????????????????C.?a≥-
且a≠0????????????????????????D.?a>-
且a≠0
6.已知关于
的方程
有实数根,则
的取值范围是
(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
且
7.关于x的一元二次方程x2+bx﹣1=0的判别式为(??
)
A.?1﹣b2??????????????????????????????????B.?b2﹣4??????????????????????????????????C.?b2+4??????????????????????????????????D.?b2+1
8.小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )
A.?????????????????B.?????????????????C.?????????????????D.?
9.已知正比例函数
,且y随x的增大而减少,则直线
的图像是(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
10.如图,在以
为原点的平面直角坐标系中,矩形
的两边
、
分别在
轴、
轴的正半轴上,反比例函数
的图象与
相交于点
,与
相交于点
,若
,且
的面积是
,则
的值为(??
).
A.???????????????????????????????????????????B.?8??????????????????????????????????????????C.?6??????????????????????????????????????????D.?
二、填空题(共6题;共18分)
11.一元二次方程(x-1)(x+2)=2(x+2)的根是________。
12.若两个最简二次根式
与
能够合并,则mn=________。
13.计算
的结果是________.
14.命题“如果
互为相反数,那么
”的逆命题为________.
15.如图,AD垂直平分BC于点D,?EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB=________.
16.如图,正方形ABCD的面积为3cm2
,
E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB
,
DC相交于点M
,
N
.
若MN=AE
,
则AM的长等于________cm
.
三、计算题(共2题;共16分)
17.计算:
(1)
(2)
18.解下列方程:
(1)
;
(2)
,
四、解答题(共5题;共36分)
19.(5分)如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、AC于点E、点D,∠A=36°.求证:AD=BC.
20.(5分)如图,在
中,
,求
的长
21.(5分)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍
,图书馆离宿舍
.周末,小亮从宿舍出发,匀速走了
到食堂;在食堂停留
吃早餐后,匀速走了
到图书馆;在图书馆停留
借书后,匀速走了
返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离
与离开宿舍的时间
之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
________
0.7
________
________
(2)填空:
①食堂到图书馆的距离为________
.
②小亮从食堂到图书馆的速度为________
.
③小亮从图书馆返回宿舍的速度为________
.
④当小亮离宿舍的距离为
时,他离开宿舍的时间为________
.
(3)当
时,请直接写出y关于x的函数解析式.
22.(6分)如图,已知反比例函数
的图象与正比例函数的图象交于
两点,且点A在第二象限,点A的横坐标为
.过点A作
轴,垂足为点
的面积为
.
(1)求反比例函数的表达式;
(2)若点P是这个反比例函数图象上的点,且
的面积是
面积的
倍,求点P的坐标.
23.(7分)如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上,连接BD.
(1)求证:△AEC≌△BDC;
(2)求证:AE2+AD2=2AC2;
(3)如图2,过点C作CO垂直AB于O点并延长交DE于点F,请直接写出线段AE、AF、DF间的数量关系(不用证明)________.
24.(8分)如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1)出发3s后,求PB的长;
(2)当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
参考答案
单选题
1
2
3
4
5
6
7
8
9
10
C
C
A
A
D
C
C
C
D
D
二、填空题
11.
x1=-2,x2=3
12.
10
13.
14.
如果
,那么
互为相反数
15.
20cm
16.
或
三、计算题
17.
(1)解:原式
.
(2)解:原式
.
18.
(1)解:
,
,
,
,
,
即
;
(2)解:
,
,
,即
,
或
,
或
,
即
.
四、解答题
19.
证明:∵AB的垂直平分线分别交AB、AC于点E、点D,
∴DB=DA,
∴△ABD是等腰三角形;
∵∠A=36°,
∴∠ABD=∠A=36°,∠ABC=∠C=(180°﹣36°)÷2=72°,
∴∠BDC=∠A+∠ABD=72°,
∴∠C=∠BDC,
∴BD=BC,
∴AD=BC.
20.
解:
,
,
,
在
中,
,
,
,
,
,
,
即BC的长为
.
21.
(1)0.5;0.7;1
(2)0.3;0.06;0.1;6或62
(3)解:当
时,
;
当
时,
当
时,设
,将(23,0.7)(28,1)代入解析式
,解得
∴
.
22.
(1)解:
反比例函数
的图象与正比例函数的图象交于A,B两点,
点A与点B关于原点对称,
,
,
,
而
,
,
反比例函数解析式为
;
(2)解:把
代入
得
,
点坐标为
,
设正比例函数解析式为
,
把
代入得
,
正比例函数解析式为
;
设P点坐标为
,
点坐标为
,
,
的面积是
面积的2倍,即
的面积为4,
,解得
或
,
当
时,
,此时P点坐标为
;
当
时,
,此时P点坐标为
,
综上所述,点P坐标为
或
.
23.
(1)证明:连接
,
,
,
在
和
中,
,
;
(2)证明:
,
,
,
又
,
.
在
中,由勾股定理可知
,
同理,在
中,
,
又
,
,
.
(3)
24.
(1)解:当t=3时,则AP=3,
∵AB=16cm,
∴PB=AB﹣AP=16﹣3=13(cm)
(2)解:由题意可知AP=t,BQ=2t,
∵AB=16,
∴BP=AB﹣AP=16﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即16﹣t=2t,解得t=
,
∴出发
秒后△PQB能形成等腰三角形;
(3)解:①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则
,
∴
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
同课章节目录
