苏科版九年级下册数学 6.6图形的位似 同步练习试卷(Word版含解析)
文档属性
| 名称 | 苏科版九年级下册数学 6.6图形的位似 同步练习试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
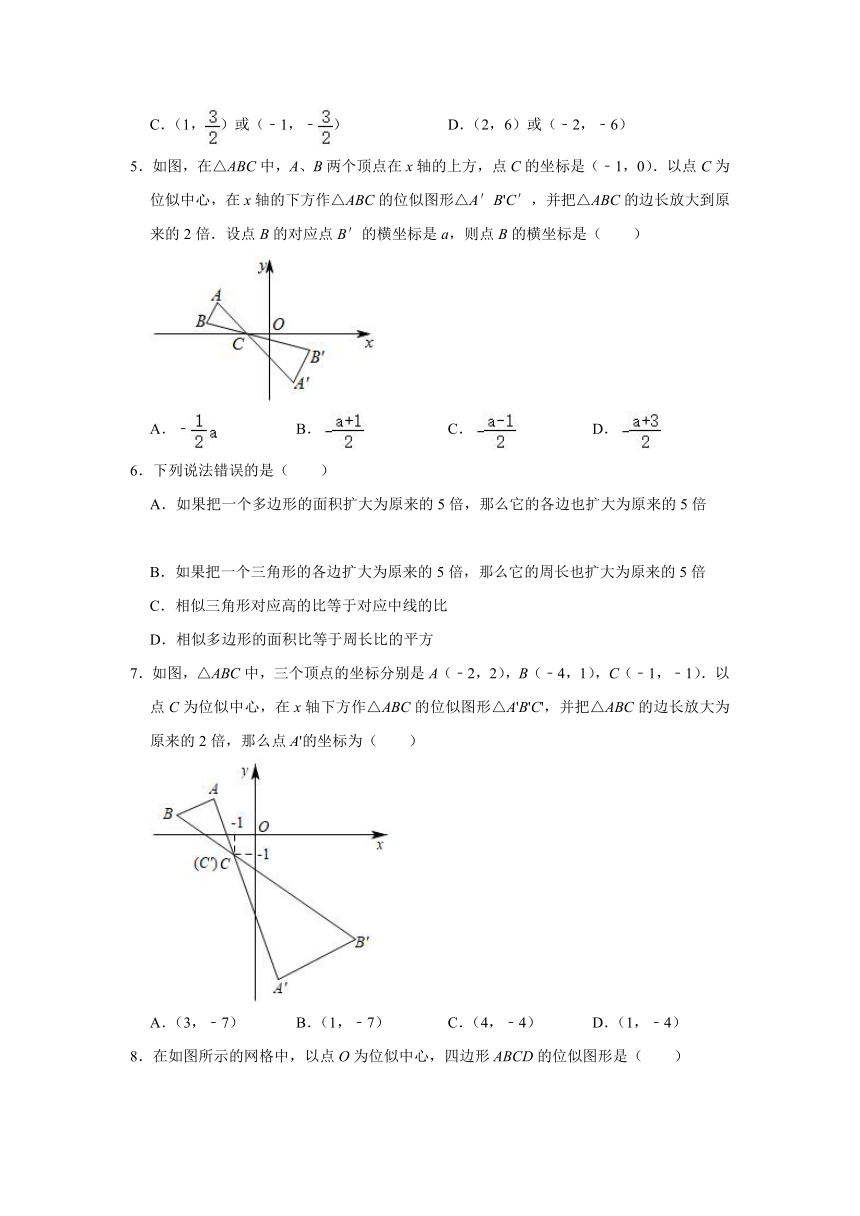
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
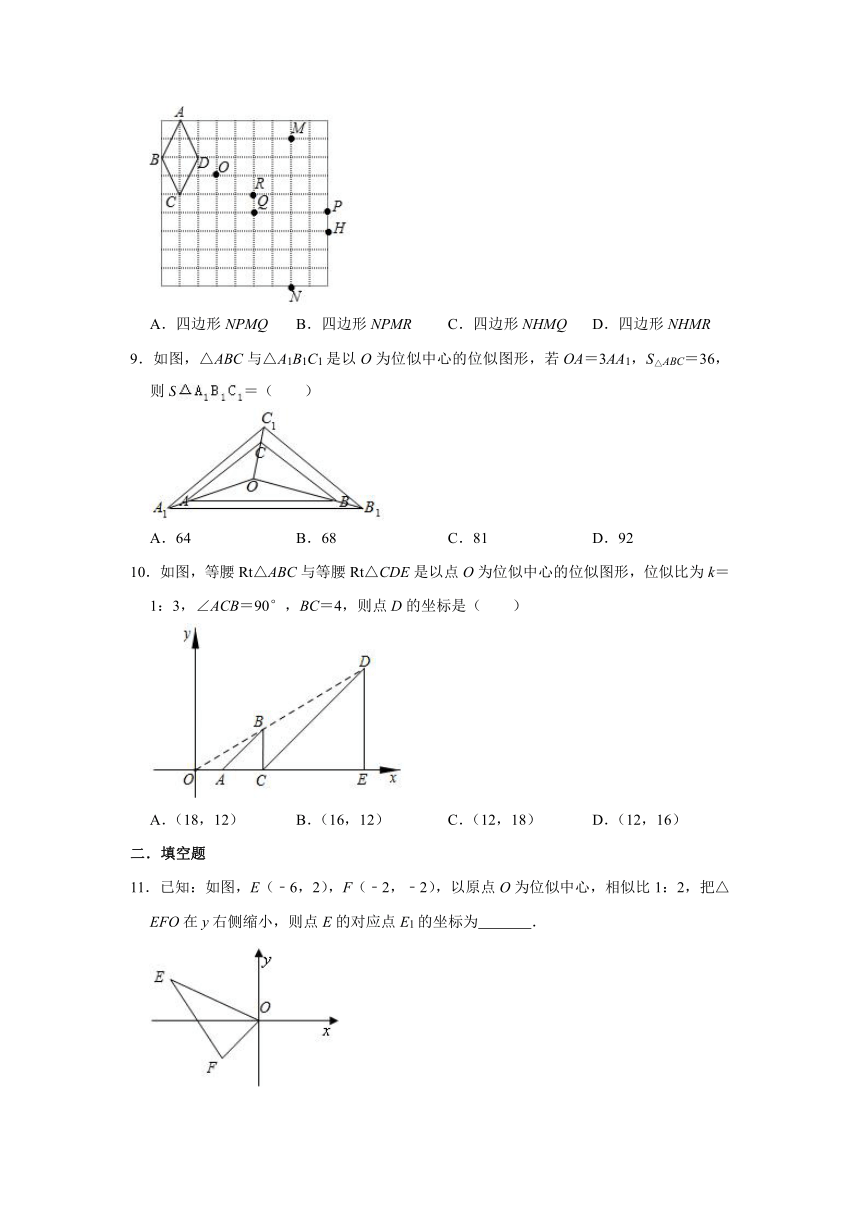
| 更新时间 | 2021-01-14 11:46:49 | ||
图片预览

文档简介
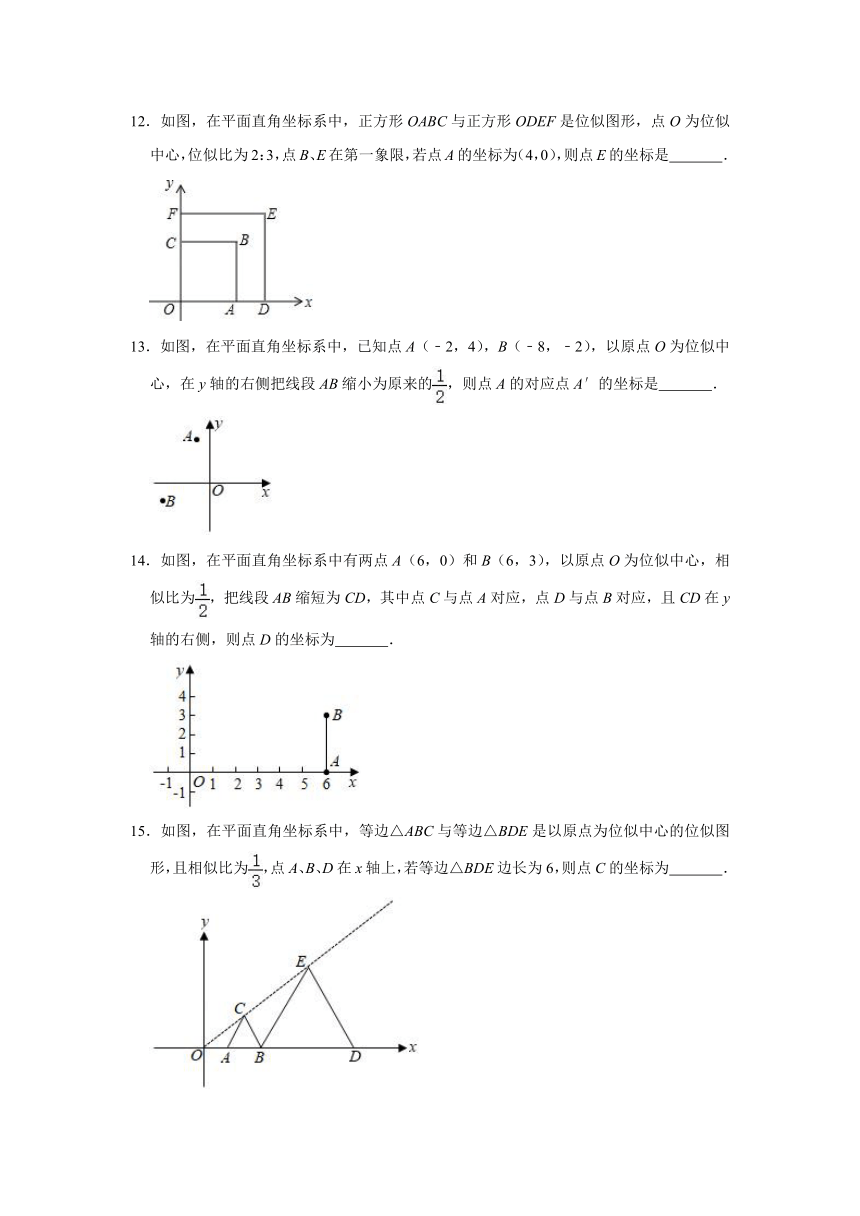
6.6图形的位似
同步练习
一.选择题
1.如图,正方形ABCD和正方形EFOG是位似图形,其中点A与点E对应,点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),则这两个正方形位似中心的坐标为( )
A.(2,0)
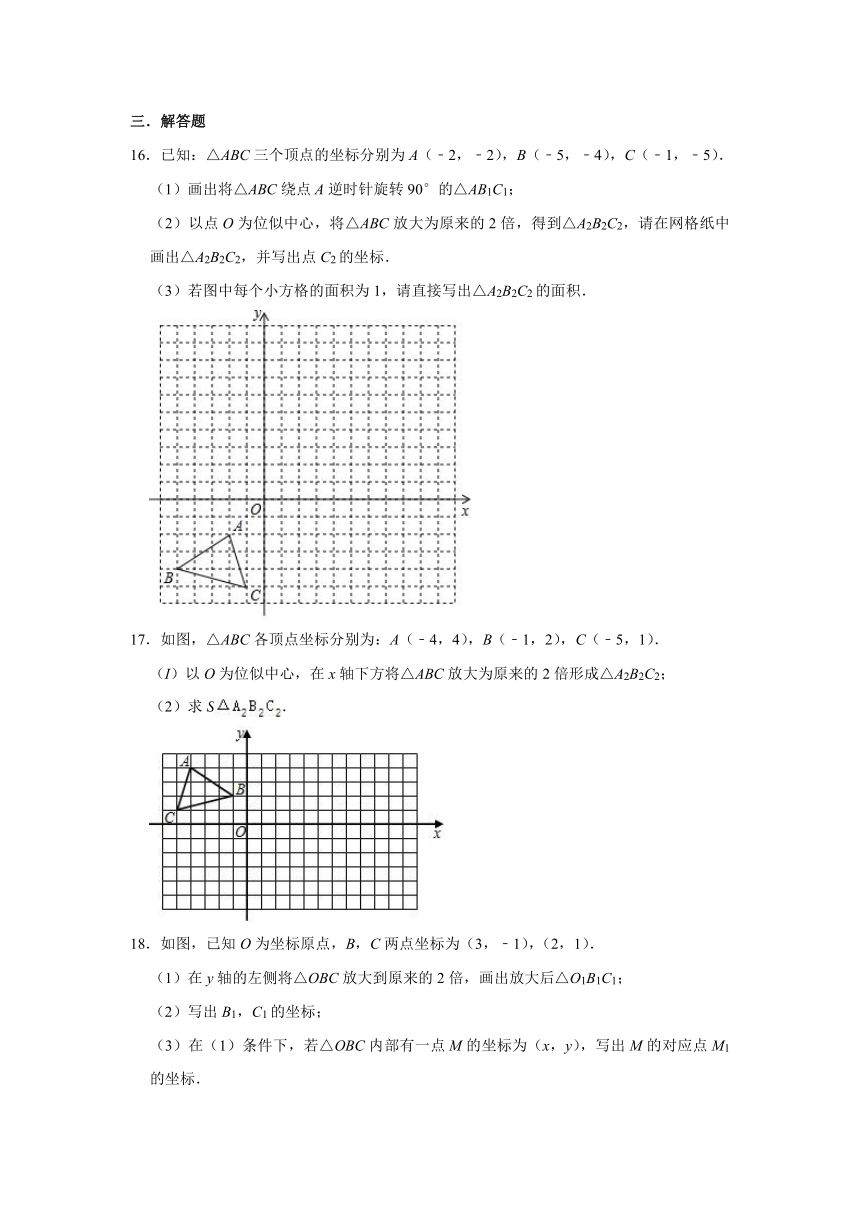
B.(1,1)
C.(﹣2,0)
D.(﹣1,0)
2.如图,六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,O为位似中心,OD=OD1,则A1B1:AB为( )
A.2:3
B.3:2
C.1:2
D.2:1
3.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心,若OB:OB'=2:3,则四边形ABCD与四边形A'B'C′D'的面积比为( )
A.2:3
B.2:5
C.4:9
D.4:25
4.在平面直角坐标系中,△ABC顶点A(2,3),若以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的相似比为1:2,则A′的坐标为( )
A.(1,)
B.(2,6)
C.(1,)或(﹣1,﹣)
D.(2,6)或(﹣2,﹣6)
5.如图,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B'C′,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A.﹣
B.
C.
D.
6.下列说法错误的是( )
A.如果把一个多边形的面积扩大为原来的5倍,那么它的各边也扩大为原来的5倍
B.如果把一个三角形的各边扩大为原来的5倍,那么它的周长也扩大为原来的5倍
C.相似三角形对应高的比等于对应中线的比
D.相似多边形的面积比等于周长比的平方
7.如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7)
B.(1,﹣7)
C.(4,﹣4)
D.(1,﹣4)
8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
9.如图,△ABC与△A1B1C1是以O为位似中心的位似图形,若OA=3AA1,S△ABC=36,则S=( )
A.64
B.68
C.81
D.92
10.如图,等腰Rt△ABC与等腰Rt△CDE是以点O为位似中心的位似图形,位似比为k=1:3,∠ACB=90°,BC=4,则点D的坐标是( )
A.(18,12)
B.(16,12)
C.(12,18)
D.(12,16)
二.填空题
11.已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为
.
12.如图,在平面直角坐标系中,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(4,0),则点E的坐标是
.
13.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,在y轴的右侧把线段AB缩小为原来的,则点A的对应点A′的坐标是
.
14.如图,在平面直角坐标系中有两点A(6,0)和B(6,3),以原点O为位似中心,相似比为,把线段AB缩短为CD,其中点C与点A对应,点D与点B对应,且CD在y轴的右侧,则点D的坐标为
.
15.如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为,点A、B、D在x轴上,若等边△BDE边长为6,则点C的坐标为
.
三.解答题
16.已知:△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)画出将△ABC绕点A逆时针旋转90°的△AB1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格纸中画出△A2B2C2,并写出点C2的坐标.
(3)若图中每个小方格的面积为1,请直接写出△A2B2C2的面积.
17.如图,△ABC各顶点坐标分别为:A(﹣4,4),B(﹣1,2),C(﹣5,1).
(I)以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
(2)求S.
18.如图,已知O为坐标原点,B,C两点坐标为(3,﹣1),(2,1).
(1)在y轴的左侧将△OBC放大到原来的2倍,画出放大后△O1B1C1;
(2)写出B1,C1的坐标;
(3)在(1)条件下,若△OBC内部有一点M的坐标为(x,y),写出M的对应点M1的坐标.
参考答案
一.选择题
1.解:连接AE并延长交x轴于H,则点H为位似中心,
∵点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),
∴OF=1,OB=4,EF=1,AB=2,
∵正方形ABCD和正方形EFOG是位似图形,
∴EF∥AB,
∴△HEF∽△HAB,
∴=,即=,
解得,OH=2,
∴点H的坐标为(2,0),
故选:A.
2.解:∵六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,
∴六边形ABCDEF∽六边形A1B1C1D1E1F1,DE∥D′E′,
∴△ODE∽△OD1E1,
∴==,
∴==2:1,
故选:D.
3.解:∵四边形ABCD与四边形A'B'C'D'位似,
∴四边形ABCD∽四边形A'B'C'D',AB∥A′B′,
∴△OAB∽△OA′B′,
∴==,
∴四边形ABCD与四边形A'B'C′D'的面积比=()2=,
故选:C.
4.解:∵以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的相似比为1:2,点A(2,3),
∴A′的坐标为(2×,3×)或(﹣2×,﹣3×),即(1,)或(﹣1,﹣),
故选:C.
5.解:以点C为坐标原点建立新的坐标系,
∵点C的坐标是(﹣1,0),
∴点B′的横坐标为:a+1,
以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B'C′,
则点B在以C为坐标原点的坐标系中的横坐标为:﹣,
∴点B在原坐标系中的横坐标为:﹣﹣1=﹣,
故选:D.
6.解:A、如果把一个多边形的面积扩大为原来的5倍,那么它的各边也扩大为原来的倍,本选项说法错误,符合题意;
B、如果把一个三角形的各边扩大为原来的5倍,那么它的周长也扩大为原来的5倍,本选项说法正确,不符合题意;
C、相似三角形对应高的比等于对应中线的比,本选项说法正确,不符合题意;
D、相似多边形的面积比等于周长比的平方,本选项说法正确,不符合题意;
故选:A.
7.解:以C为坐标原点建立平面直角坐标系,则点A在新坐标系中的坐标为(﹣1,3),
∵△ABC与△A'B'C'以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',把△ABC的边长放大为原来的2倍,
∴点A'在新坐标系中的坐标为(1×2,﹣3×2),即(2,﹣6),
则点A'的坐标为(1,﹣7),
故选:B.
8.解:∵以点O为位似中心,
∴点C对应点M,
设网格中每个小方格的边长为1,
则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,
∵==2,
∴点D对应点Q,点B对应点P,点A对应点N,
∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,
故选:A.
9.解:∵△ABC与△A1B1C1是以O为位似中心的位似图形,
∴△ABC∽△A1B1C1,
∵OA=3AA1,
∴△ABC与△A1B1C1的相似比为:=,
∴△ABC与△A1B1C1的面积比为:()2=,
∵S△ABC=36,
∴S=36÷=64,
故选:A.
10.解:由题意可得:△OBC∽△ODE,
则==,
∵BC=4,
∴ED=12,
∵等腰Rt△CDE,
∴CE=DE=12,
∴=,
解得:CO=6,
故EO=18,
∴点D的坐标是(18,12).
故选:A.
二.填空题
11.解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
12.解:∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,
∴=,=,即=,=,
解得,OD=6,OF=6,
则点E的坐标为(6,6),
故答案为:(6,6).
13.解:∵以原点O为位似中心,在y轴的右侧把线段AB缩小为原来的,点A的坐标为(﹣2,4),
∴点A的对应点A′的坐标为(﹣2×(﹣),4×(﹣)),即(1,﹣2),
故答案为:(1,﹣2).
14.解:∵以原点O为位似中心,相似比为,把线段AB缩短为CD,CD在y轴的右侧,点B的坐标为(6,3),
∴点D的坐标为(6×,3×),即(3,),
故答案为:(3,).
15.解:作CF⊥AB于F,
∵等边△ABC与等边△BDE是以原点为位似中心的位似图形,
∴BC∥DE,
∴△OBC∽△ODE,
∴=,
∵△ABC与△BDE的相似比为,等边△BDE边长为6,
∴==,
解得,BC=2,OB=3,
∴OA=1,
∵CA=CB,CF⊥AB,
∴AF=1,
由勾股定理得,CF==,
∴OF=OA+AF=2,
∴点C的坐标为(2,),
故答案为:(2,).
三.解答题
16.解:(1)如图,△AB1C1为所作;
(2)如图,△A2B2C2为所作;点C2的坐标为(2,10).
(3)△A2B2C2的面积=4S△ABC=4(4×3﹣×1×3﹣×3×2﹣×1×4)=22.
17.解:(1)如图,△A2B2C2为所作;
(2)S=6×8﹣×6×2﹣×8×2﹣×4×6=22.
18.解:(1)如图,△O1B1C1即为所求作.
(2)B1(﹣6,2),C1(﹣4,﹣2).
(3)M1
(﹣2x,﹣2y).
同步练习
一.选择题
1.如图,正方形ABCD和正方形EFOG是位似图形,其中点A与点E对应,点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),则这两个正方形位似中心的坐标为( )
A.(2,0)
B.(1,1)
C.(﹣2,0)
D.(﹣1,0)
2.如图,六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,O为位似中心,OD=OD1,则A1B1:AB为( )
A.2:3
B.3:2
C.1:2
D.2:1
3.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心,若OB:OB'=2:3,则四边形ABCD与四边形A'B'C′D'的面积比为( )
A.2:3
B.2:5
C.4:9
D.4:25
4.在平面直角坐标系中,△ABC顶点A(2,3),若以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的相似比为1:2,则A′的坐标为( )
A.(1,)
B.(2,6)
C.(1,)或(﹣1,﹣)
D.(2,6)或(﹣2,﹣6)
5.如图,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B'C′,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A.﹣
B.
C.
D.
6.下列说法错误的是( )
A.如果把一个多边形的面积扩大为原来的5倍,那么它的各边也扩大为原来的5倍
B.如果把一个三角形的各边扩大为原来的5倍,那么它的周长也扩大为原来的5倍
C.相似三角形对应高的比等于对应中线的比
D.相似多边形的面积比等于周长比的平方
7.如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7)
B.(1,﹣7)
C.(4,﹣4)
D.(1,﹣4)
8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
9.如图,△ABC与△A1B1C1是以O为位似中心的位似图形,若OA=3AA1,S△ABC=36,则S=( )
A.64
B.68
C.81
D.92
10.如图,等腰Rt△ABC与等腰Rt△CDE是以点O为位似中心的位似图形,位似比为k=1:3,∠ACB=90°,BC=4,则点D的坐标是( )
A.(18,12)
B.(16,12)
C.(12,18)
D.(12,16)
二.填空题
11.已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为
.
12.如图,在平面直角坐标系中,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(4,0),则点E的坐标是
.
13.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,在y轴的右侧把线段AB缩小为原来的,则点A的对应点A′的坐标是
.
14.如图,在平面直角坐标系中有两点A(6,0)和B(6,3),以原点O为位似中心,相似比为,把线段AB缩短为CD,其中点C与点A对应,点D与点B对应,且CD在y轴的右侧,则点D的坐标为
.
15.如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为,点A、B、D在x轴上,若等边△BDE边长为6,则点C的坐标为
.
三.解答题
16.已知:△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)画出将△ABC绕点A逆时针旋转90°的△AB1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格纸中画出△A2B2C2,并写出点C2的坐标.
(3)若图中每个小方格的面积为1,请直接写出△A2B2C2的面积.
17.如图,△ABC各顶点坐标分别为:A(﹣4,4),B(﹣1,2),C(﹣5,1).
(I)以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
(2)求S.
18.如图,已知O为坐标原点,B,C两点坐标为(3,﹣1),(2,1).
(1)在y轴的左侧将△OBC放大到原来的2倍,画出放大后△O1B1C1;
(2)写出B1,C1的坐标;
(3)在(1)条件下,若△OBC内部有一点M的坐标为(x,y),写出M的对应点M1的坐标.
参考答案
一.选择题
1.解:连接AE并延长交x轴于H,则点H为位似中心,
∵点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),
∴OF=1,OB=4,EF=1,AB=2,
∵正方形ABCD和正方形EFOG是位似图形,
∴EF∥AB,
∴△HEF∽△HAB,
∴=,即=,
解得,OH=2,
∴点H的坐标为(2,0),
故选:A.
2.解:∵六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,
∴六边形ABCDEF∽六边形A1B1C1D1E1F1,DE∥D′E′,
∴△ODE∽△OD1E1,
∴==,
∴==2:1,
故选:D.
3.解:∵四边形ABCD与四边形A'B'C'D'位似,
∴四边形ABCD∽四边形A'B'C'D',AB∥A′B′,
∴△OAB∽△OA′B′,
∴==,
∴四边形ABCD与四边形A'B'C′D'的面积比=()2=,
故选:C.
4.解:∵以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的相似比为1:2,点A(2,3),
∴A′的坐标为(2×,3×)或(﹣2×,﹣3×),即(1,)或(﹣1,﹣),
故选:C.
5.解:以点C为坐标原点建立新的坐标系,
∵点C的坐标是(﹣1,0),
∴点B′的横坐标为:a+1,
以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B'C′,
则点B在以C为坐标原点的坐标系中的横坐标为:﹣,
∴点B在原坐标系中的横坐标为:﹣﹣1=﹣,
故选:D.
6.解:A、如果把一个多边形的面积扩大为原来的5倍,那么它的各边也扩大为原来的倍,本选项说法错误,符合题意;
B、如果把一个三角形的各边扩大为原来的5倍,那么它的周长也扩大为原来的5倍,本选项说法正确,不符合题意;
C、相似三角形对应高的比等于对应中线的比,本选项说法正确,不符合题意;
D、相似多边形的面积比等于周长比的平方,本选项说法正确,不符合题意;
故选:A.
7.解:以C为坐标原点建立平面直角坐标系,则点A在新坐标系中的坐标为(﹣1,3),
∵△ABC与△A'B'C'以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',把△ABC的边长放大为原来的2倍,
∴点A'在新坐标系中的坐标为(1×2,﹣3×2),即(2,﹣6),
则点A'的坐标为(1,﹣7),
故选:B.
8.解:∵以点O为位似中心,
∴点C对应点M,
设网格中每个小方格的边长为1,
则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,
∵==2,
∴点D对应点Q,点B对应点P,点A对应点N,
∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,
故选:A.
9.解:∵△ABC与△A1B1C1是以O为位似中心的位似图形,
∴△ABC∽△A1B1C1,
∵OA=3AA1,
∴△ABC与△A1B1C1的相似比为:=,
∴△ABC与△A1B1C1的面积比为:()2=,
∵S△ABC=36,
∴S=36÷=64,
故选:A.
10.解:由题意可得:△OBC∽△ODE,
则==,
∵BC=4,
∴ED=12,
∵等腰Rt△CDE,
∴CE=DE=12,
∴=,
解得:CO=6,
故EO=18,
∴点D的坐标是(18,12).
故选:A.
二.填空题
11.解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
12.解:∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,
∴=,=,即=,=,
解得,OD=6,OF=6,
则点E的坐标为(6,6),
故答案为:(6,6).
13.解:∵以原点O为位似中心,在y轴的右侧把线段AB缩小为原来的,点A的坐标为(﹣2,4),
∴点A的对应点A′的坐标为(﹣2×(﹣),4×(﹣)),即(1,﹣2),
故答案为:(1,﹣2).
14.解:∵以原点O为位似中心,相似比为,把线段AB缩短为CD,CD在y轴的右侧,点B的坐标为(6,3),
∴点D的坐标为(6×,3×),即(3,),
故答案为:(3,).
15.解:作CF⊥AB于F,
∵等边△ABC与等边△BDE是以原点为位似中心的位似图形,
∴BC∥DE,
∴△OBC∽△ODE,
∴=,
∵△ABC与△BDE的相似比为,等边△BDE边长为6,
∴==,
解得,BC=2,OB=3,
∴OA=1,
∵CA=CB,CF⊥AB,
∴AF=1,
由勾股定理得,CF==,
∴OF=OA+AF=2,
∴点C的坐标为(2,),
故答案为:(2,).
三.解答题
16.解:(1)如图,△AB1C1为所作;
(2)如图,△A2B2C2为所作;点C2的坐标为(2,10).
(3)△A2B2C2的面积=4S△ABC=4(4×3﹣×1×3﹣×3×2﹣×1×4)=22.
17.解:(1)如图,△A2B2C2为所作;
(2)S=6×8﹣×6×2﹣×8×2﹣×4×6=22.
18.解:(1)如图,△O1B1C1即为所求作.
(2)B1(﹣6,2),C1(﹣4,﹣2).
(3)M1
(﹣2x,﹣2y).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
