六年级数学下册课件-4.2.2 反比例人教版(共43张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.2.2 反比例人教版(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
(共43张PPT)
正比例和反比例
反比例
(1)X∶Y=K,k一定,成正比例。
(2)Y×X=K,k一定,成反比例。
正比例和反比例的认识
(3)正比例,两种相关联的量,一个
量变化,另外一个量也随之变化,
如果这两个的比值一定,就是正
比例。
正比例和反比例的认识
(4)反比例,两种相关联的量,一种
变化,另外一种也随之变化,如
果这两个量的乘积一定,那么就
是反比例。
正比例和反比例的认识
正比例和反比例的变化规律
(1)正比例会因为一个量的扩大,
另一个数也随之扩大。
(2)反比例一个量扩大,会引起
另一个量的缩小。
生活中的量
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
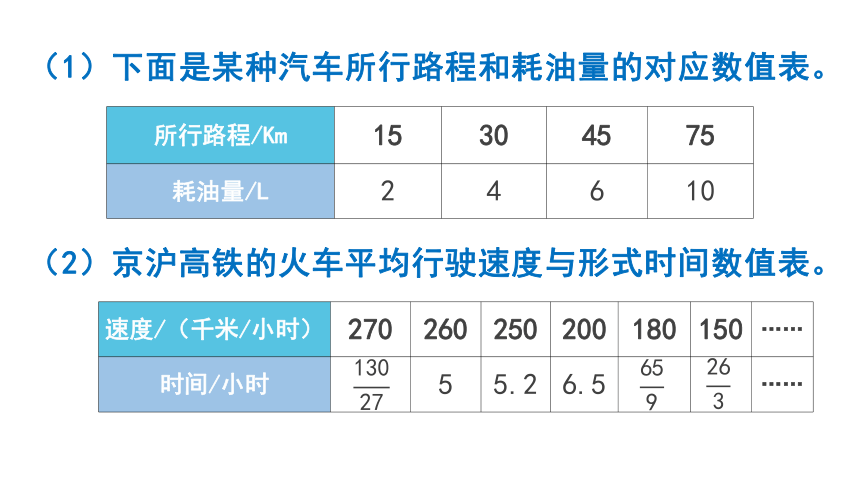
(1)下面是某种汽车所行路程和耗油量的对应数值表。
速度/(千米/小时)
270
260
250
200
180
150
……
时间/小时
5
5.2
6.5
……
(2)京沪高铁的火车平均行驶速度与形式时间数值表。
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
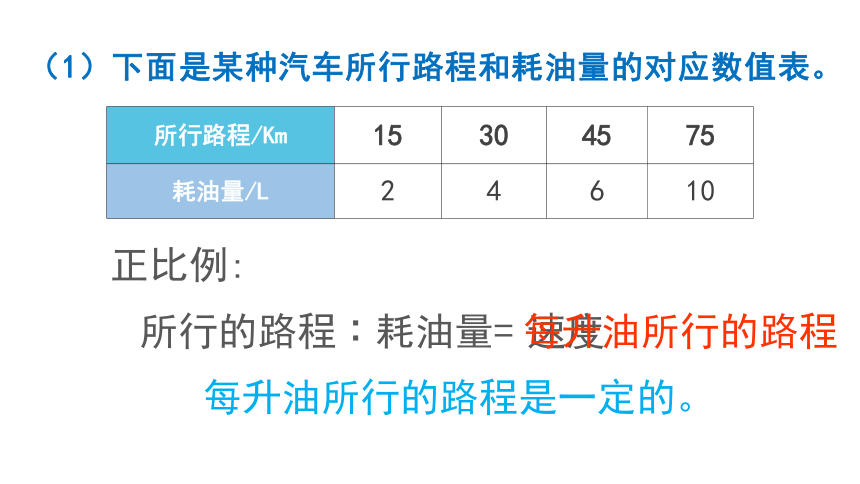
(1)下面是某种汽车所行路程和耗油量的对应数值表。
正比例:
所行的路程∶耗油量=
速度
每升油所行的路程
每升油所行的路程是一定的。
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
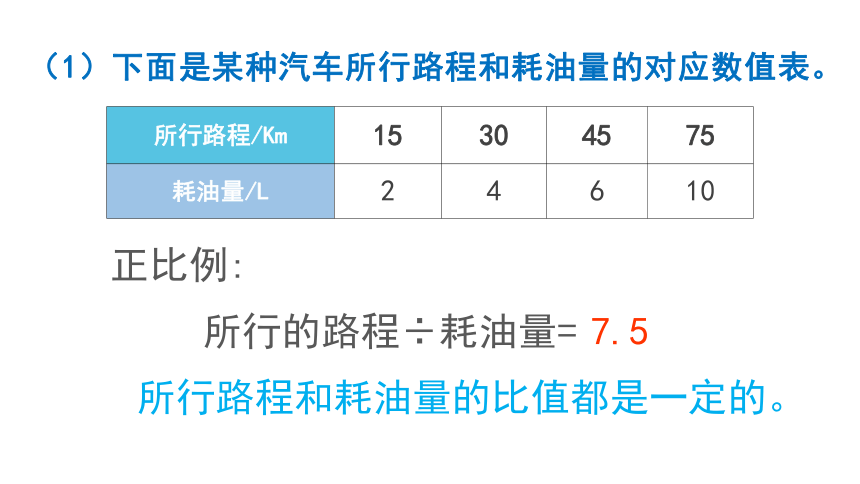
(1)下面是某种汽车所行路程和耗油量的对应数值表。
正比例:
所行的路程÷耗油量=
7.5
所行路程和耗油量的比值都是一定的。
速度/(千米/小时)
270
260
250
200
180
150
……
时间/小时
5
5.2
6.5
……
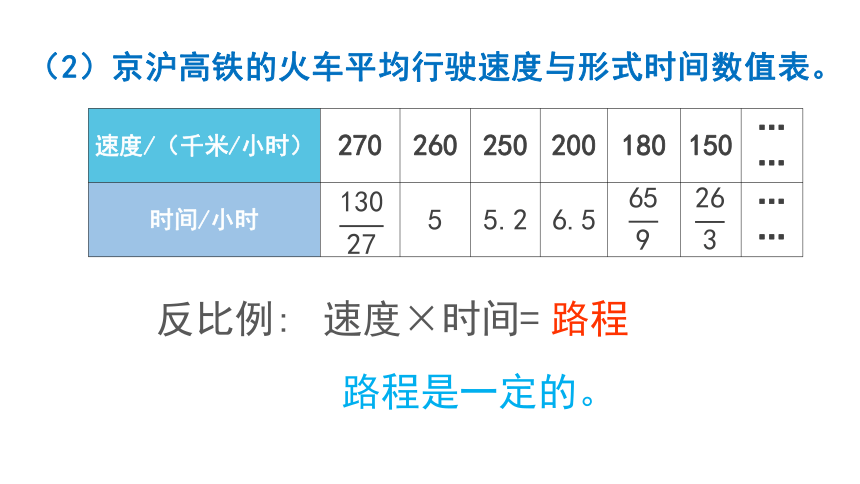
(2)京沪高铁的火车平均行驶速度与形式时间数值表。
反比例:
速度×时间=
路程是一定的。
路程
(1)煤的总量一定,使用天数与每天的平均用煤量。
判断下面每题中的两种量成什么比例关系?并用关系式或列表等方式说明你作出判断的依据。
(2)《小学生作文》的单价一定,订阅的费用与订
阅的数量。
(3)书的总页数一定,已读的页数与未读的页数。
使用天数×每天的平均用煤量=煤的总量
所以使用天数与每天平均用的量成反比例。
煤的总量一定,使用天数与每天的平均用煤量。
煤的总量一定,使用天数与每天的平均用煤量。
使用天数
平均用煤量
煤的总量是一定的。
1
10
2
5
3
4
2.5
5
2
规律总结
(1)借助于解决的关系式。
(2)通过列表,很直观的发现两种量之间
存在的规律。
订阅费用∶订阅量=单价
所以订阅费用与订阅数量成正比例。
《小学生作文》的单价一定,订阅的费用与订阅的数量。
不成比例。
已读页数+未读的页数=书的总页数。
书的总页数一定,已读的页数与未读的页数。
正比例
反比例
不成比例
X
Y
10
30
20
15
有两个相关联的量X、Y
反比例:
10×30=300
20×15=300
乘积一定,成反比例。
X
Y
10
30
20
60
有两个相关联的量X、Y
正比例:
10∶30=3
20∶60=3
X
Y
10
30
20
60
有两个相关联的量X、Y
0.6
1200
1.8
400
X、Y成正比例关系
X
Y
10
30
20
15
有两个相关联的量X、Y,X、Y成反比例关系。
0.6
1200
500
0.25
乘积一定,都等于300。
X
Y
10
30
20
60
有两个相关联的量X、Y
比值一定。
正比例:
X
Y
10
30
20
15
有两个相关联的量X、Y
乘积一定。
反比例:
X
Y
10
30
20
20
有两个相关联的量X、Y
和一定。
不成立,
X
Y
10
30
20
40
有两个相关联的量X、Y
差一定。
不成立,
生活当中,两种相关联的量,可能成正比例,可能成反比例,也可能不成立。
例题讲解
树高/米
2
3
6
影长/米
1.6
2.4
4.8
同一时间,同一地点测得3棵树的树高及其影长如下表。
树高/米
2
3
6
影长/米
1.6
2.4
4.8
在图中描出表示树高与对应影长的点,然后把它们连起来。观察图像,影长与树高成什么比例关系?你是依据什么作出判断的?
0
1
2
3
4
5
6
7
0.8
1.6
2.4
3.2
4.0
4.8
同一时间,树高比影长的比值,都是0.8,0.8一定。
(1)树高2米的时候,它
的影长是1.6,比值
0.8。
(2)树高6米的时候,它
的影长是4.8,比值
也是0.8。
树高和影长成正比例。
测量学校旗杆的高度
利用生活中树高与影长成正比例关系,小组合作设计测量学校旗杆高度的方案。
(1)在同一时间里,让一名同学站在阳光下,
量出他的影长和身高,得到相应比例;然
后,同一时间量出旗杆的影长;最后,通
过正比例关系式,测出旗杆高度。
同学身高∶同学影长=X∶旗杆影长
旗杆高度
测量学校旗杆的高度
测量学校旗杆的高度
(2)第一步,找一个参照物—树,量出它的高
度和影长;第二步,判断它成什么比例,
算出比值;第三步,量出旗杆的影长,用
正比例的方法,求出旗杆的高度。
利用正比例关系式
正比例
同一时间、同一地点
离旗杆近的树
旗杆附近没有树
(3)使用尺子来当参照物。
(4)使用竹竿来当参照物,绑在旗杆上,或者立在
旗杆旁。
利用正比例的关系,比值一定,量出旗杆影长,算出旗杆高度。
测量学校旗杆的高度
你真棒!
给我一个支点,我就可以翘起地球。
杠杆原理
研究杠杆原理背后的数学知识。
要想左右保持平衡,右边也要挂6颗,应该挂在哪里?
20
15
10
5
5
10
15
20
8
如果我在左边刻度8挂上了6颗棋子。
20
15
10
5
5
10
15
20
8
如果我在左边刻度8挂上了6颗棋子。
在右边的刻度8挂上6颗棋子。
8
左边重
右边重
20
15
10
5
5
10
15
20
6
如果我在左边刻度6挂上了4颗棋子。
为了保持平衡,右
边的棋子可以怎么放呢?
20
15
10
5
5
10
15
20
6
如果我在左边刻度6挂上了4颗棋子。
(1)在刻度8放3颗。
(2)在刻度12放2颗。
右刻度
1
2
3
4
6
8
12
所放棋子
乘积
如果我在左边刻度6挂上了4颗棋子,为了保持平衡,右边的棋子可以怎么放呢?
24
24
12
24
24
24
24
24
24
8
6
4
3
2
反比例:格子数乘以所放的棋子数,等于乘积,乘
积一定。
发现了什么?
右边的刻度×所放棋子数=左边的刻度×所放棋子数
乘积一定,所以成反比例关系。
杠杆原理背后隐藏着反比例。
刻度×棋子的颗数=乘积,乘积(一定)
成反比例
在生活中,也存在着正比例和反比例。
杠杆原理
杠杆原理背后就是反比例
树高和影长是成正比例。
利用树高和影长:
解决生活中没有办法直接测量的东西的高度。
再
见!
正比例和反比例
反比例
(1)X∶Y=K,k一定,成正比例。
(2)Y×X=K,k一定,成反比例。
正比例和反比例的认识
(3)正比例,两种相关联的量,一个
量变化,另外一个量也随之变化,
如果这两个的比值一定,就是正
比例。
正比例和反比例的认识
(4)反比例,两种相关联的量,一种
变化,另外一种也随之变化,如
果这两个量的乘积一定,那么就
是反比例。
正比例和反比例的认识
正比例和反比例的变化规律
(1)正比例会因为一个量的扩大,
另一个数也随之扩大。
(2)反比例一个量扩大,会引起
另一个量的缩小。
生活中的量
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
(1)下面是某种汽车所行路程和耗油量的对应数值表。
速度/(千米/小时)
270
260
250
200
180
150
……
时间/小时
5
5.2
6.5
……
(2)京沪高铁的火车平均行驶速度与形式时间数值表。
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
(1)下面是某种汽车所行路程和耗油量的对应数值表。
正比例:
所行的路程∶耗油量=
速度
每升油所行的路程
每升油所行的路程是一定的。
所行路程/Km
15
30
45
75
耗油量/L
2
4
6
10
(1)下面是某种汽车所行路程和耗油量的对应数值表。
正比例:
所行的路程÷耗油量=
7.5
所行路程和耗油量的比值都是一定的。
速度/(千米/小时)
270
260
250
200
180
150
……
时间/小时
5
5.2
6.5
……
(2)京沪高铁的火车平均行驶速度与形式时间数值表。
反比例:
速度×时间=
路程是一定的。
路程
(1)煤的总量一定,使用天数与每天的平均用煤量。
判断下面每题中的两种量成什么比例关系?并用关系式或列表等方式说明你作出判断的依据。
(2)《小学生作文》的单价一定,订阅的费用与订
阅的数量。
(3)书的总页数一定,已读的页数与未读的页数。
使用天数×每天的平均用煤量=煤的总量
所以使用天数与每天平均用的量成反比例。
煤的总量一定,使用天数与每天的平均用煤量。
煤的总量一定,使用天数与每天的平均用煤量。
使用天数
平均用煤量
煤的总量是一定的。
1
10
2
5
3
4
2.5
5
2
规律总结
(1)借助于解决的关系式。
(2)通过列表,很直观的发现两种量之间
存在的规律。
订阅费用∶订阅量=单价
所以订阅费用与订阅数量成正比例。
《小学生作文》的单价一定,订阅的费用与订阅的数量。
不成比例。
已读页数+未读的页数=书的总页数。
书的总页数一定,已读的页数与未读的页数。
正比例
反比例
不成比例
X
Y
10
30
20
15
有两个相关联的量X、Y
反比例:
10×30=300
20×15=300
乘积一定,成反比例。
X
Y
10
30
20
60
有两个相关联的量X、Y
正比例:
10∶30=3
20∶60=3
X
Y
10
30
20
60
有两个相关联的量X、Y
0.6
1200
1.8
400
X、Y成正比例关系
X
Y
10
30
20
15
有两个相关联的量X、Y,X、Y成反比例关系。
0.6
1200
500
0.25
乘积一定,都等于300。
X
Y
10
30
20
60
有两个相关联的量X、Y
比值一定。
正比例:
X
Y
10
30
20
15
有两个相关联的量X、Y
乘积一定。
反比例:
X
Y
10
30
20
20
有两个相关联的量X、Y
和一定。
不成立,
X
Y
10
30
20
40
有两个相关联的量X、Y
差一定。
不成立,
生活当中,两种相关联的量,可能成正比例,可能成反比例,也可能不成立。
例题讲解
树高/米
2
3
6
影长/米
1.6
2.4
4.8
同一时间,同一地点测得3棵树的树高及其影长如下表。
树高/米
2
3
6
影长/米
1.6
2.4
4.8
在图中描出表示树高与对应影长的点,然后把它们连起来。观察图像,影长与树高成什么比例关系?你是依据什么作出判断的?
0
1
2
3
4
5
6
7
0.8
1.6
2.4
3.2
4.0
4.8
同一时间,树高比影长的比值,都是0.8,0.8一定。
(1)树高2米的时候,它
的影长是1.6,比值
0.8。
(2)树高6米的时候,它
的影长是4.8,比值
也是0.8。
树高和影长成正比例。
测量学校旗杆的高度
利用生活中树高与影长成正比例关系,小组合作设计测量学校旗杆高度的方案。
(1)在同一时间里,让一名同学站在阳光下,
量出他的影长和身高,得到相应比例;然
后,同一时间量出旗杆的影长;最后,通
过正比例关系式,测出旗杆高度。
同学身高∶同学影长=X∶旗杆影长
旗杆高度
测量学校旗杆的高度
测量学校旗杆的高度
(2)第一步,找一个参照物—树,量出它的高
度和影长;第二步,判断它成什么比例,
算出比值;第三步,量出旗杆的影长,用
正比例的方法,求出旗杆的高度。
利用正比例关系式
正比例
同一时间、同一地点
离旗杆近的树
旗杆附近没有树
(3)使用尺子来当参照物。
(4)使用竹竿来当参照物,绑在旗杆上,或者立在
旗杆旁。
利用正比例的关系,比值一定,量出旗杆影长,算出旗杆高度。
测量学校旗杆的高度
你真棒!
给我一个支点,我就可以翘起地球。
杠杆原理
研究杠杆原理背后的数学知识。
要想左右保持平衡,右边也要挂6颗,应该挂在哪里?
20
15
10
5
5
10
15
20
8
如果我在左边刻度8挂上了6颗棋子。
20
15
10
5
5
10
15
20
8
如果我在左边刻度8挂上了6颗棋子。
在右边的刻度8挂上6颗棋子。
8
左边重
右边重
20
15
10
5
5
10
15
20
6
如果我在左边刻度6挂上了4颗棋子。
为了保持平衡,右
边的棋子可以怎么放呢?
20
15
10
5
5
10
15
20
6
如果我在左边刻度6挂上了4颗棋子。
(1)在刻度8放3颗。
(2)在刻度12放2颗。
右刻度
1
2
3
4
6
8
12
所放棋子
乘积
如果我在左边刻度6挂上了4颗棋子,为了保持平衡,右边的棋子可以怎么放呢?
24
24
12
24
24
24
24
24
24
8
6
4
3
2
反比例:格子数乘以所放的棋子数,等于乘积,乘
积一定。
发现了什么?
右边的刻度×所放棋子数=左边的刻度×所放棋子数
乘积一定,所以成反比例关系。
杠杆原理背后隐藏着反比例。
刻度×棋子的颗数=乘积,乘积(一定)
成反比例
在生活中,也存在着正比例和反比例。
杠杆原理
杠杆原理背后就是反比例
树高和影长是成正比例。
利用树高和影长:
解决生活中没有办法直接测量的东西的高度。
再
见!
