34.4二次函数的应用(1)课件
图片预览



文档简介
(共9张PPT)
34.4二次函数的应用(1)
义务教育课程标准试验教材(冀教版)
九年级下册
河北教育出版社
二次函数有着广泛的应用,利用二次函数的图
像,我们可以求出一元二次方程的近似解,通过建
立二次函数模型并利用它的有关性质,还可以解决
一些实际问题.
驶向胜利的彼岸
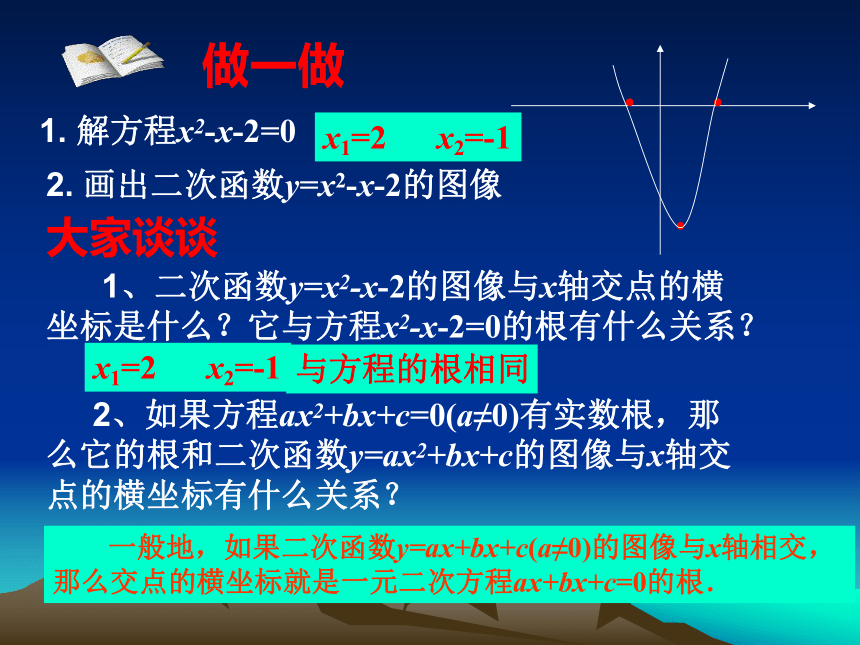
做一做
1.
解方程x2-x-2=0
2.
画出二次函数y=x2-x-2的图像
大家谈谈
1、二次函数y=x2-x-2的图像与x轴交点的横
坐标是什么?它与方程x2-x-2=0的根有什么关系?
2、如果方程ax2+bx+c=0(a≠0)有实数根,那
么它的根和二次函数y=ax2+bx+c的图像与x轴交
点的横坐标有什么关系?
一般地,如果二次函数y=ax+bx+c(a≠0)的图像与x轴相交,
那么交点的横坐标就是一元二次方程ax+bx+c=0的根.
x1=2
x2=-1
x1=2
x2=-1
与方程的根相同
一起研究:
已知二次函数y=x2+x-1.
1.
观察这个函数的图像,一元二次方程
x2+x-1=0的两个根分别在哪两个整数之间?
2.(1)由在0至1范围内的x值所对应的y值
(见下表),你能说出一元二次方程x2+x-1=0
精确到十分位的正根吗?
x
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
y
-1
-0.89
-0.76
-0.61
-0.44
-0.25
-0.04
0.19
0.44
0.71
1
x
y
1
2
3
-1
-2
-1
-2
1
2
(2)由0.6至0.7范围内的x值所对应的y值(见下表),你能说出一元二次方程x2+x-1=0精确到十分位的正根吗?
x
0.60
0.61
0.62
0.63
0.64
0.65
y
-0.040
-0.018
0.004
0.027
0.050
0.073
x
0.66
0.67
0.68
0.69
0.70
y
0.096
0.119
0.42
0.166
0.190
3.
请仿照上面的方法,求出一元二次方程x2+x-1=0的另一个精确到十分位的根.
4.
请利用一元二次方程的求根公式解方程x2+x-1=0,
并验证上面求出的近似解.
我们发现,当二次函数y=ax2+bx+c(a≠0)的图像与x轴有交点时,根据图像与x轴的交点,就可以确定一元二次方程ax2+bx+c=0的根在哪两个连续整数之间,为了得到更精确的近似值,对在这两个连续整数之间的x值进行细分,并求出相应的y值,列出表格,这样就可以得到一元二次方程ax2+bx+c=0所要求的精确度的近似值.
练习
已知一个矩形的长比宽多3m,面积为6m2,求这个矩形的长(精确到十分位).
解:
设矩形的长为
x
m,则宽为(x-3)m,
依题意得:
x(x-3)=6
即x2-3x-6=0
令y=x2-3x-6,则此二次函数的图像为:
x
y
1
2
3
-1
-2
-2
2
4
5
所以x介于4和5之间,见下表:
x
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
y
-2
-1.49
-0.96
-0.41
0.16
0.75
所以x介于4.3和4.4之间,见下表:
x
4.30
4.31
4.32
4.33
4.34
4.35
y
-0.41
-0.35
-030
-0.24
-0.18
-0.13
x
4.36
4.37
4.38
4.39
4.40
y
-0.07
所以
x≈4.4
作业:
课本:第20页
习题
1、2
预习下一节内容.
下课了!
驶向胜利的彼岸
34.4二次函数的应用(1)
义务教育课程标准试验教材(冀教版)
九年级下册
河北教育出版社
二次函数有着广泛的应用,利用二次函数的图
像,我们可以求出一元二次方程的近似解,通过建
立二次函数模型并利用它的有关性质,还可以解决
一些实际问题.
驶向胜利的彼岸
做一做
1.
解方程x2-x-2=0
2.
画出二次函数y=x2-x-2的图像
大家谈谈
1、二次函数y=x2-x-2的图像与x轴交点的横
坐标是什么?它与方程x2-x-2=0的根有什么关系?
2、如果方程ax2+bx+c=0(a≠0)有实数根,那
么它的根和二次函数y=ax2+bx+c的图像与x轴交
点的横坐标有什么关系?
一般地,如果二次函数y=ax+bx+c(a≠0)的图像与x轴相交,
那么交点的横坐标就是一元二次方程ax+bx+c=0的根.
x1=2
x2=-1
x1=2
x2=-1
与方程的根相同
一起研究:
已知二次函数y=x2+x-1.
1.
观察这个函数的图像,一元二次方程
x2+x-1=0的两个根分别在哪两个整数之间?
2.(1)由在0至1范围内的x值所对应的y值
(见下表),你能说出一元二次方程x2+x-1=0
精确到十分位的正根吗?
x
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
y
-1
-0.89
-0.76
-0.61
-0.44
-0.25
-0.04
0.19
0.44
0.71
1
x
y
1
2
3
-1
-2
-1
-2
1
2
(2)由0.6至0.7范围内的x值所对应的y值(见下表),你能说出一元二次方程x2+x-1=0精确到十分位的正根吗?
x
0.60
0.61
0.62
0.63
0.64
0.65
y
-0.040
-0.018
0.004
0.027
0.050
0.073
x
0.66
0.67
0.68
0.69
0.70
y
0.096
0.119
0.42
0.166
0.190
3.
请仿照上面的方法,求出一元二次方程x2+x-1=0的另一个精确到十分位的根.
4.
请利用一元二次方程的求根公式解方程x2+x-1=0,
并验证上面求出的近似解.
我们发现,当二次函数y=ax2+bx+c(a≠0)的图像与x轴有交点时,根据图像与x轴的交点,就可以确定一元二次方程ax2+bx+c=0的根在哪两个连续整数之间,为了得到更精确的近似值,对在这两个连续整数之间的x值进行细分,并求出相应的y值,列出表格,这样就可以得到一元二次方程ax2+bx+c=0所要求的精确度的近似值.
练习
已知一个矩形的长比宽多3m,面积为6m2,求这个矩形的长(精确到十分位).
解:
设矩形的长为
x
m,则宽为(x-3)m,
依题意得:
x(x-3)=6
即x2-3x-6=0
令y=x2-3x-6,则此二次函数的图像为:
x
y
1
2
3
-1
-2
-2
2
4
5
所以x介于4和5之间,见下表:
x
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
y
-2
-1.49
-0.96
-0.41
0.16
0.75
所以x介于4.3和4.4之间,见下表:
x
4.30
4.31
4.32
4.33
4.34
4.35
y
-0.41
-0.35
-030
-0.24
-0.18
-0.13
x
4.36
4.37
4.38
4.39
4.40
y
-0.07
所以
x≈4.4
作业:
课本:第20页
习题
1、2
预习下一节内容.
下课了!
驶向胜利的彼岸
