第三章 图形的平移与旋转 单元测试 培优卷(含解析)
文档属性
| 名称 | 第三章 图形的平移与旋转 单元测试 培优卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章
图形的平移与旋转
单元测试培优卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积(
)
A.不变
B.先增大再减小
C.先减小再增大
D.不断增大
2.如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B,C旋转后的对应点分别是B′和C′,连接BB′,则∠ABB′的度数是( )
A.35°
B.40°
C.45°
D.55°
3.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5)
B.(1,0)
C.(1,-1)
D.(1.5,-0.5)
4.如图,将边长为4的等边三角形OAB先向下平移3个单位长度,再将平移后的图形沿y轴翻折,经过两次变换后,点A的对应点A′的坐标为( )
A.(2,3-2
)
B.(2,1)
C.(-2,2
-3)
D.(-1,2
)
5.已知点P关于x轴的对称点P1的坐标是(4,3),那么点P关于原点的对称点P2的坐标是()
A.(-3,-4)
B.(-4,3)
C.(-4,-3)
D.(4,-3)
6.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比(
)
A.向右平移了3个单位
B.向左平移了3个单位
C.向上平移了3个单位
D.向下平移了3个单位
7.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是(
?
)
A.16cm
B.18cm
C.20cm
D.21cm
8.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( ).
A.60
°
B.75°
C.85°
D.90°
9.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是
( )
A.垂直
B.相等
C.平分
D.平分且垂直
10.如图,面积为12cm2的△ABC沿BC方向平移到△DEF的位置,平移的距离是边BC长的2倍,则图中四边形ACED的面积为( )
A.24cm2
B.36cm2
C.48cm2
D.无法确定
二、填空题.(共8小题,每小题3分,满分24分)
11.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=______.
12.如图,把等边三角形绕点O旋转,至少要旋转___________度后与原来的图形重合.
13.如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC=________,旋转角度是__________.
14.如图,E为正方形ABCD内一点,∠AEB=135?,BE=3cm,△AEB按顺时针方向旋转一个角度后成为△CFB,图中________是旋转中心,旋转_______度.
15.如图,△ABC、△ADE均为是顶角为42?的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______.
16.如图所示,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A′B′C′的位置.若平移的距离为2,则图中阴影部分的面积为________.
17.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为__________.
18.如图,将线段AB沿箭头方向平移2
cm得到线段CD,若AB=3
cm,则四边形ABDC的周长为___cm.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
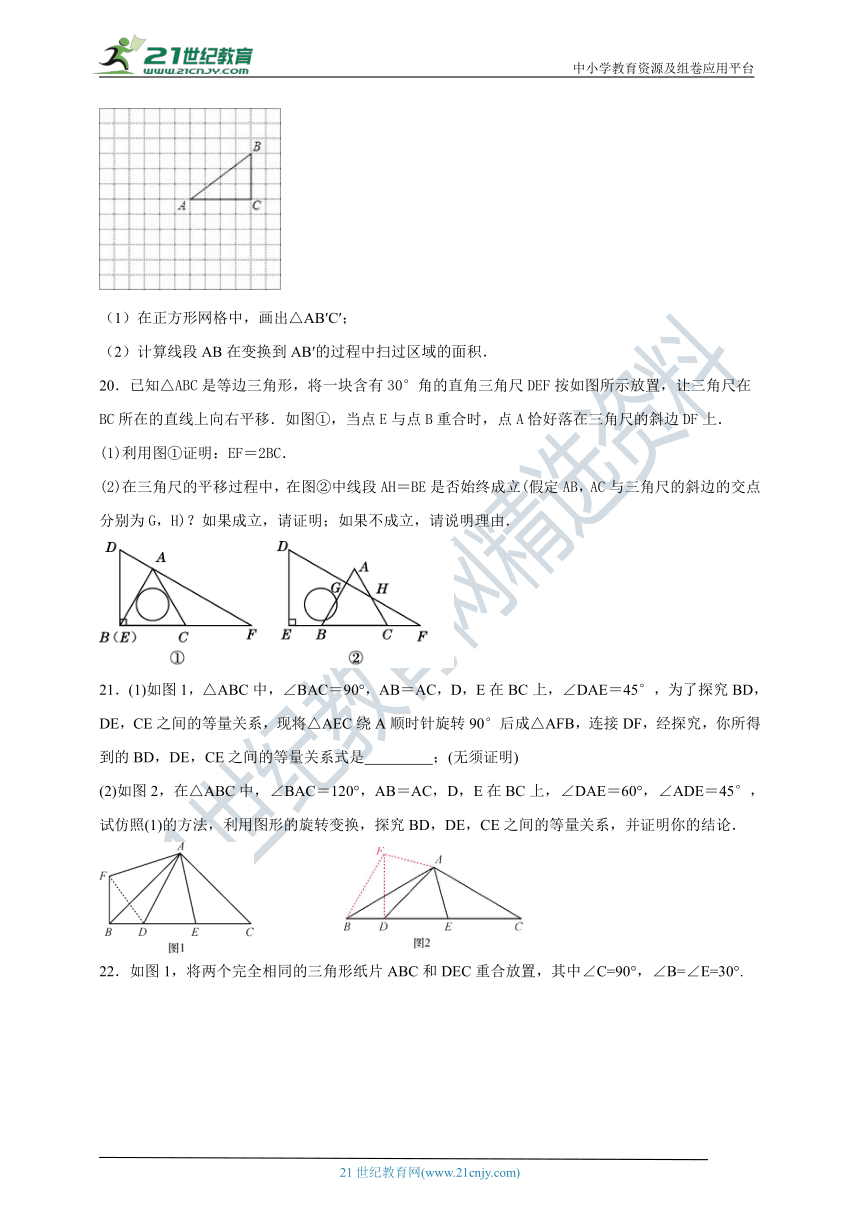
19.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
20.已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图①,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图①证明:EF=2BC.
(2)在三角尺的平移过程中,在图②中线段AH=BE是否始终成立(假定AB,AC与三角尺的斜边的交点分别为G,H)?如果成立,请证明;如果不成立,请说明理由.
21.(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是
;(无须证明)
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
22.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是
;
②设△BDC的面积为S1,△AEC的面积为S2.则S1与S2的数量关系是
.
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF=S△BDC,请直接写出相应的BF的长
23.如图点O是等边内一点,,∠ACD=∠BCO,OC=CD,
(1)试说明:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)当为多少度时,是等腰三角形
参考答案
1.A
【详解】
∵四边形ABCD、四边形OEFG是两个边长相等正方形,
∴∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,
∴∠BOC-∠COM=∠EOG-∠COM,
即∠BOM=∠CON,
∵在△BOM和△CON中
,
∴△BOM≌△CON,
∴两个正方形的重叠部分四边形OMCN的面积是
S△COM+S△CNO=S△COM+S△BOM=S△BOC=S正方形ABCD,
即不论旋转多少度,阴影部分的面积都等于S正方形ABCD,
故选A.
2.D
【详解】
由旋转可得,AB=AB',∠BAB'=70°,
∴∠ABB'=∠AB'B=(180°-∠BAB′)=55°.
故选:D.
3.C
【详解】
∵△ABC绕旋转中心顺时针旋转90°后得到△A?B?C?,∴A、B的对应点分别是A?、B?.
又∵线段BB?的垂直平分线为x=1,线段AA?是一个边长为3的正方形的对角线,其垂直平分线是另一条对角线所在的直线,由图形可知,线段BB?与AA?的垂直平分线的交点为(1,﹣1).
故选C.
4.C
【详解】
解:∵等边三角形OAB边长为4,
∴A(2,2),
∵先向下平移3个单位,
∴A点对应点坐标为(2,2?3),
∵再将平移后的图形沿y轴翻折,
∴这时A的对应点坐标为(?2,2?3),
故选C.
5.B
【详解】
∵点P关于x轴的对称点P1的坐标是(4,3),
∴P点坐标为(4,-3),
∴点P(4,-3)关于原点的对称点P2的坐标是(-4,3).
故选B.
6.D
【详解】
∵将三角形各点的纵坐标都减去3,横坐标保持不变,
∴所得图形与原图形相比向下平移了3个单位.
故选D.
7.C
【解析】
试题分析:已知,△ABE向右平移2cm得到△DCF,根据平移的性质得到EF=AD=2cm,AE=DF,又因△ABE的周长为16cm,所以AB+BC+AC=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.故答案选C.
8.C
【解析】
试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.
如图,设AD⊥BC于点F.则∠AFB=90°,
∴在Rt△ABF中,∠B=90°-∠BAD=25°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,
即∠BAC的度数为85°.故选C.
9.D
【详解】
解:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O.
∵A′O=OB=,AO=OC=2,
∴线段A′B与线段AC互相平分,
又∵∠AOA′=45°+45°=90°,
∴A′B⊥AC,
∴线段A′B与线段AC互相垂直平分.
故选D.
10.B
【解析】
试题分析:由题意可知根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可.
∵平移的距离是边BC长的两倍,
∴BC=CE=EF,
∴四边形ACED的面积是三个△ABC的面积;
∴四边形ACED的面积=12×3=36cm2.
11.80°或120°
【详解】
解:如图,在线段AB取一点B′,使DB=DB′,在线段AC取一点B″,使DB=DB″,
∴①旋转角m=∠BDB′=180°-∠DB′B-∠B=180°-2∠B=80°,
②在Rt△B″CD中,∵DB″=DB=2CD,
∴∠CDB″=60°,
旋转角∠BDB″=180°-∠CDB″=120°.
故答案为80°或120°.
12.120
【详解】
旋转中心为点O,
根据等边三角形的性质可知,
OA=OB=OC,∠AOB=∠BOC=∠COA=120°,
所以,至少旋转120度后能与原来图形重合,
故答案为:120.
13.155°
25°
【详解】
在△ABC中,已知∠A=15°,∠C=10°,
∴∠ABC=180°-∠A-∠C=155°;
又∵点B为旋转中心,E的对应点为A,
∴旋转角为∠ABE=180°-∠ABC=25°,
故答案为155°,25°.
14.B
90°
【详解】
∵△AEB按顺时针方向旋转一个角度后成为△CFB,
BA旋转到了BC,
∴旋转中心为点B,旋转角为∠ABC,
∵四边形ABCD是正方形,
∴∠ABC=90°,
即旋转了90°角,
故答案为:B,90.
15.ABD
ACE
A
42°
【详解】
∵△ABC、△ADE均为是顶角为42?的等腰三角形,BC和DE分别是底边,
∴AB=AC,AD=AE,∠BAC=∠DAE=42°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∴△BAD≌△CAE,
∴图中△ABD可以通过旋转得到△ACE,旋转中心为A,旋转角度为42°,
故答案为:ABD,ACE,A,
42°.
16.8
解:∵∠C=90°,AC=BC=5,平移的距离为2,
∴BC′=DC′=3
∴阴影面积=5×5÷2-3×3÷2=8.
故答案为:8.
17.126°
【详解】
∵正三角形ABC与正三角形CDE
∴CD=CE,BC=AC,
∠DEC=∠EDC=∠DCE=60°
∴∠EDC-∠BCD=∠DCE-∠BCD
∴∠BCE=∠DCA
在△BCE和△ADC中;
∴△BCE△ADC
∴∠ADC=∠BEC;
∵∠BEC=∠BED+∠DEC=∠BED+60°;
∴∠ADC=∠BED+60°
在△BDE中,∠BDE=180°-∠DBE-∠BED=180°-66°-∠BED=114°-∠BED
∴∠ADB=360°-∠ADC-∠BDE-∠EDC=360°-(∠BED+60°)-(114°-∠BED)-60°=126°
故答案为:126°
18.10cm
【解析】
根据平移的性质得:AB=CD=3,AC=BD=2,则四边形ABDC的周长3+3+2+2=10.
19.(1)见解析;(2)π.
【详解】
(1)解:如图所示:△AB′C′即为所求
(2)解:∵AB=
=5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:=π
20.(1)详见解析;(2)成立,证明见解析.
【详解】
(1)∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.
∵∠F=30°,∴∠CAF=60°-30°=30°,∴∠CAF=∠F,∴CF=AC,∴CF=AC=BC,∴EF=2BC.
(2)成立.证明如下:
∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.
∵∠F=30°,∴∠CHF=60°-30°=30°,∴∠CHF=∠F,∴CH=CF.
∵EF=2BC,∴BE+CF=BC.
又∵AH+CH=AC,AC=BC,∴AH=BE.
21.(1)
BD2+CE2=DE2;
(2)
BD2+DE2=CE2,证明见解析.
【详解】
(1)
BD2+CE2=DE2;
(2)CE2=BD2+DE2.
证明:将△AEC绕点A顺时针旋转120
°得到△AFB,连接FD.
由旋转的性质可得△AEC≌△AFB,∴AF=AE,BF=CE,∠FAB=∠EAC.
∴∠FAE=∠FAB+∠BAE=∠EAC+∠BAE=∠BAC=120
°.
又∵∠DAE=60
°,
∴∠FAD=∠EAD=60
°.
在△ADF和△ADE中,
∴△ADF≌△ADE(SAS).
∴FD=DE,∠ADF=∠ADE.
∵∠ADE=45
°,
∴∠ADF=45
°,故∠BDF=90
°.
在Rt△BDF中,由勾股定理,得BF2=BD2+DF2.
∴CE2=BD2+DE2.
22.解:(1)①DE∥AC.②.(2)仍然成立,证明见解析;(3)3或6.
【详解】
(1)①由旋转可知:AC=DC,
∵∠C=90°,∠B=∠DCE=30°,∴∠DAC=∠CDE=60°.∴△ADC是等边三角形.
∴∠DCA=60°.∴∠DCA=∠CDE=60°.∴DE∥AC.
②过D作DN⊥AC交AC于点N,过E作EM⊥AC交AC延长线于M,过C作CF⊥AB交AB于点F.
由①可知:△ADC是等边三角形,
DE∥AC,∴DN=CF,DN=EM.
∴CF=EM.
∵∠C=90°,∠B
=30°
∴AB=2AC.
又∵AD=AC
∴BD=AC.
∵
∴.
(2)如图,过点D作DM⊥BC于M,过点A作AN⊥CE交EC的延长线于N,
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,
所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,过点D作DG⊥BC于G,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB=×60°=30°,BG=BC=,
∴BD=3
∴∠CDF1=180°-∠BCD=180°-30°=150°,
∠CDF2=360°-150°-60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
,
∴△CDF1≌△CDF2(SAS),
∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,
∴∠DBC=∠BDE=∠ABD=×60°=30°,
又∵BD=3,
∴BE=×3÷cos30°=3,
∴BF1=3,BF2=BF1+F1F2=3+3=6,
故BF的长为3或6.
23.(1)见解析;(2)△AOD是直角三角形,理由见解析;(3)
110°或125°或140°时,△AOD是等腰三角形.
【详解】
(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC?∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α?60°,∠AOD=360°?60°?110°?α=190°?α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°?α=α?60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°?α)+α?60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°?α+2(α?60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第三章
图形的平移与旋转
单元测试培优卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积(
)
A.不变
B.先增大再减小
C.先减小再增大
D.不断增大
2.如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B,C旋转后的对应点分别是B′和C′,连接BB′,则∠ABB′的度数是( )
A.35°
B.40°
C.45°
D.55°
3.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5)
B.(1,0)
C.(1,-1)
D.(1.5,-0.5)
4.如图,将边长为4的等边三角形OAB先向下平移3个单位长度,再将平移后的图形沿y轴翻折,经过两次变换后,点A的对应点A′的坐标为( )
A.(2,3-2
)
B.(2,1)
C.(-2,2
-3)
D.(-1,2
)
5.已知点P关于x轴的对称点P1的坐标是(4,3),那么点P关于原点的对称点P2的坐标是()
A.(-3,-4)
B.(-4,3)
C.(-4,-3)
D.(4,-3)
6.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比(
)
A.向右平移了3个单位
B.向左平移了3个单位
C.向上平移了3个单位
D.向下平移了3个单位
7.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是(
?
)
A.16cm
B.18cm
C.20cm
D.21cm
8.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( ).
A.60
°
B.75°
C.85°
D.90°
9.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是
( )
A.垂直
B.相等
C.平分
D.平分且垂直
10.如图,面积为12cm2的△ABC沿BC方向平移到△DEF的位置,平移的距离是边BC长的2倍,则图中四边形ACED的面积为( )
A.24cm2
B.36cm2
C.48cm2
D.无法确定
二、填空题.(共8小题,每小题3分,满分24分)
11.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=______.
12.如图,把等边三角形绕点O旋转,至少要旋转___________度后与原来的图形重合.
13.如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC=________,旋转角度是__________.
14.如图,E为正方形ABCD内一点,∠AEB=135?,BE=3cm,△AEB按顺时针方向旋转一个角度后成为△CFB,图中________是旋转中心,旋转_______度.
15.如图,△ABC、△ADE均为是顶角为42?的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______.
16.如图所示,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A′B′C′的位置.若平移的距离为2,则图中阴影部分的面积为________.
17.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为__________.
18.如图,将线段AB沿箭头方向平移2
cm得到线段CD,若AB=3
cm,则四边形ABDC的周长为___cm.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
19.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
20.已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图①,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图①证明:EF=2BC.
(2)在三角尺的平移过程中,在图②中线段AH=BE是否始终成立(假定AB,AC与三角尺的斜边的交点分别为G,H)?如果成立,请证明;如果不成立,请说明理由.
21.(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是
;(无须证明)
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
22.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是
;
②设△BDC的面积为S1,△AEC的面积为S2.则S1与S2的数量关系是
.
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF=S△BDC,请直接写出相应的BF的长
23.如图点O是等边内一点,,∠ACD=∠BCO,OC=CD,
(1)试说明:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)当为多少度时,是等腰三角形
参考答案
1.A
【详解】
∵四边形ABCD、四边形OEFG是两个边长相等正方形,
∴∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,
∴∠BOC-∠COM=∠EOG-∠COM,
即∠BOM=∠CON,
∵在△BOM和△CON中
,
∴△BOM≌△CON,
∴两个正方形的重叠部分四边形OMCN的面积是
S△COM+S△CNO=S△COM+S△BOM=S△BOC=S正方形ABCD,
即不论旋转多少度,阴影部分的面积都等于S正方形ABCD,
故选A.
2.D
【详解】
由旋转可得,AB=AB',∠BAB'=70°,
∴∠ABB'=∠AB'B=(180°-∠BAB′)=55°.
故选:D.
3.C
【详解】
∵△ABC绕旋转中心顺时针旋转90°后得到△A?B?C?,∴A、B的对应点分别是A?、B?.
又∵线段BB?的垂直平分线为x=1,线段AA?是一个边长为3的正方形的对角线,其垂直平分线是另一条对角线所在的直线,由图形可知,线段BB?与AA?的垂直平分线的交点为(1,﹣1).
故选C.
4.C
【详解】
解:∵等边三角形OAB边长为4,
∴A(2,2),
∵先向下平移3个单位,
∴A点对应点坐标为(2,2?3),
∵再将平移后的图形沿y轴翻折,
∴这时A的对应点坐标为(?2,2?3),
故选C.
5.B
【详解】
∵点P关于x轴的对称点P1的坐标是(4,3),
∴P点坐标为(4,-3),
∴点P(4,-3)关于原点的对称点P2的坐标是(-4,3).
故选B.
6.D
【详解】
∵将三角形各点的纵坐标都减去3,横坐标保持不变,
∴所得图形与原图形相比向下平移了3个单位.
故选D.
7.C
【解析】
试题分析:已知,△ABE向右平移2cm得到△DCF,根据平移的性质得到EF=AD=2cm,AE=DF,又因△ABE的周长为16cm,所以AB+BC+AC=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.故答案选C.
8.C
【解析】
试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.
如图,设AD⊥BC于点F.则∠AFB=90°,
∴在Rt△ABF中,∠B=90°-∠BAD=25°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,
即∠BAC的度数为85°.故选C.
9.D
【详解】
解:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O.
∵A′O=OB=,AO=OC=2,
∴线段A′B与线段AC互相平分,
又∵∠AOA′=45°+45°=90°,
∴A′B⊥AC,
∴线段A′B与线段AC互相垂直平分.
故选D.
10.B
【解析】
试题分析:由题意可知根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可.
∵平移的距离是边BC长的两倍,
∴BC=CE=EF,
∴四边形ACED的面积是三个△ABC的面积;
∴四边形ACED的面积=12×3=36cm2.
11.80°或120°
【详解】
解:如图,在线段AB取一点B′,使DB=DB′,在线段AC取一点B″,使DB=DB″,
∴①旋转角m=∠BDB′=180°-∠DB′B-∠B=180°-2∠B=80°,
②在Rt△B″CD中,∵DB″=DB=2CD,
∴∠CDB″=60°,
旋转角∠BDB″=180°-∠CDB″=120°.
故答案为80°或120°.
12.120
【详解】
旋转中心为点O,
根据等边三角形的性质可知,
OA=OB=OC,∠AOB=∠BOC=∠COA=120°,
所以,至少旋转120度后能与原来图形重合,
故答案为:120.
13.155°
25°
【详解】
在△ABC中,已知∠A=15°,∠C=10°,
∴∠ABC=180°-∠A-∠C=155°;
又∵点B为旋转中心,E的对应点为A,
∴旋转角为∠ABE=180°-∠ABC=25°,
故答案为155°,25°.
14.B
90°
【详解】
∵△AEB按顺时针方向旋转一个角度后成为△CFB,
BA旋转到了BC,
∴旋转中心为点B,旋转角为∠ABC,
∵四边形ABCD是正方形,
∴∠ABC=90°,
即旋转了90°角,
故答案为:B,90.
15.ABD
ACE
A
42°
【详解】
∵△ABC、△ADE均为是顶角为42?的等腰三角形,BC和DE分别是底边,
∴AB=AC,AD=AE,∠BAC=∠DAE=42°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∴△BAD≌△CAE,
∴图中△ABD可以通过旋转得到△ACE,旋转中心为A,旋转角度为42°,
故答案为:ABD,ACE,A,
42°.
16.8
解:∵∠C=90°,AC=BC=5,平移的距离为2,
∴BC′=DC′=3
∴阴影面积=5×5÷2-3×3÷2=8.
故答案为:8.
17.126°
【详解】
∵正三角形ABC与正三角形CDE
∴CD=CE,BC=AC,
∠DEC=∠EDC=∠DCE=60°
∴∠EDC-∠BCD=∠DCE-∠BCD
∴∠BCE=∠DCA
在△BCE和△ADC中;
∴△BCE△ADC
∴∠ADC=∠BEC;
∵∠BEC=∠BED+∠DEC=∠BED+60°;
∴∠ADC=∠BED+60°
在△BDE中,∠BDE=180°-∠DBE-∠BED=180°-66°-∠BED=114°-∠BED
∴∠ADB=360°-∠ADC-∠BDE-∠EDC=360°-(∠BED+60°)-(114°-∠BED)-60°=126°
故答案为:126°
18.10cm
【解析】
根据平移的性质得:AB=CD=3,AC=BD=2,则四边形ABDC的周长3+3+2+2=10.
19.(1)见解析;(2)π.
【详解】
(1)解:如图所示:△AB′C′即为所求
(2)解:∵AB=
=5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:=π
20.(1)详见解析;(2)成立,证明见解析.
【详解】
(1)∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.
∵∠F=30°,∴∠CAF=60°-30°=30°,∴∠CAF=∠F,∴CF=AC,∴CF=AC=BC,∴EF=2BC.
(2)成立.证明如下:
∵△ABC是等边三角形,∴∠ACB=60°,AC=BC.
∵∠F=30°,∴∠CHF=60°-30°=30°,∴∠CHF=∠F,∴CH=CF.
∵EF=2BC,∴BE+CF=BC.
又∵AH+CH=AC,AC=BC,∴AH=BE.
21.(1)
BD2+CE2=DE2;
(2)
BD2+DE2=CE2,证明见解析.
【详解】
(1)
BD2+CE2=DE2;
(2)CE2=BD2+DE2.
证明:将△AEC绕点A顺时针旋转120
°得到△AFB,连接FD.
由旋转的性质可得△AEC≌△AFB,∴AF=AE,BF=CE,∠FAB=∠EAC.
∴∠FAE=∠FAB+∠BAE=∠EAC+∠BAE=∠BAC=120
°.
又∵∠DAE=60
°,
∴∠FAD=∠EAD=60
°.
在△ADF和△ADE中,
∴△ADF≌△ADE(SAS).
∴FD=DE,∠ADF=∠ADE.
∵∠ADE=45
°,
∴∠ADF=45
°,故∠BDF=90
°.
在Rt△BDF中,由勾股定理,得BF2=BD2+DF2.
∴CE2=BD2+DE2.
22.解:(1)①DE∥AC.②.(2)仍然成立,证明见解析;(3)3或6.
【详解】
(1)①由旋转可知:AC=DC,
∵∠C=90°,∠B=∠DCE=30°,∴∠DAC=∠CDE=60°.∴△ADC是等边三角形.
∴∠DCA=60°.∴∠DCA=∠CDE=60°.∴DE∥AC.
②过D作DN⊥AC交AC于点N,过E作EM⊥AC交AC延长线于M,过C作CF⊥AB交AB于点F.
由①可知:△ADC是等边三角形,
DE∥AC,∴DN=CF,DN=EM.
∴CF=EM.
∵∠C=90°,∠B
=30°
∴AB=2AC.
又∵AD=AC
∴BD=AC.
∵
∴.
(2)如图,过点D作DM⊥BC于M,过点A作AN⊥CE交EC的延长线于N,
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,
所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,过点D作DG⊥BC于G,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB=×60°=30°,BG=BC=,
∴BD=3
∴∠CDF1=180°-∠BCD=180°-30°=150°,
∠CDF2=360°-150°-60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
,
∴△CDF1≌△CDF2(SAS),
∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,
∴∠DBC=∠BDE=∠ABD=×60°=30°,
又∵BD=3,
∴BE=×3÷cos30°=3,
∴BF1=3,BF2=BF1+F1F2=3+3=6,
故BF的长为3或6.
23.(1)见解析;(2)△AOD是直角三角形,理由见解析;(3)
110°或125°或140°时,△AOD是等腰三角形.
【详解】
(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC?∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α?60°,∠AOD=360°?60°?110°?α=190°?α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°?α=α?60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°?α)+α?60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°?α+2(α?60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
