15.1.2幂的乘方
图片预览






文档简介
(共15张PPT)
1、叙述同底数幂乘法法则
同底数幂相乘底数不变,指数相加。
2、用字母表示同底数幂乘法法则
am·an=am+n
3、计算:①a2·a5·an;②a4·a4·a4
①a2+5+n
②a12
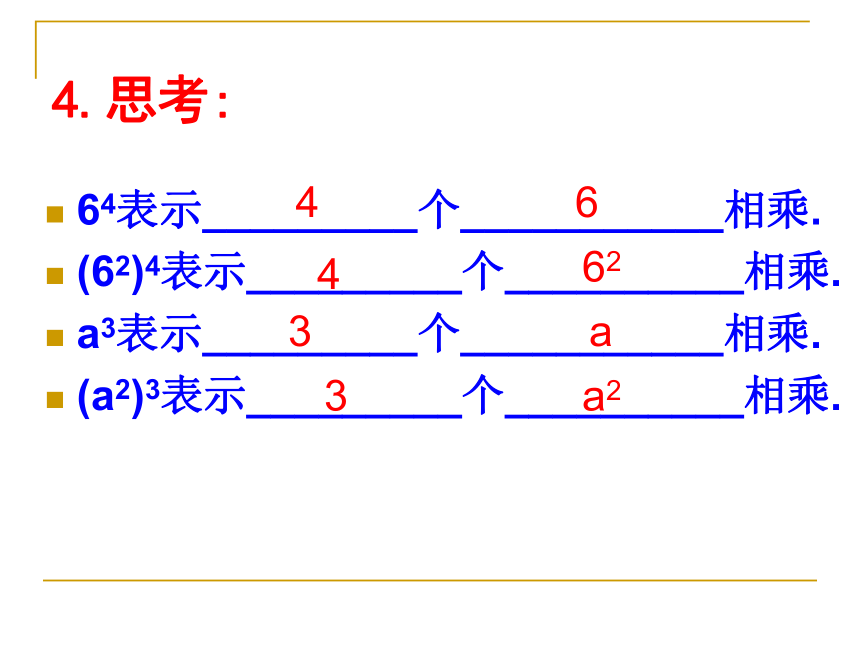
4.思考:
64表示_________个___________相乘.
(62)4表示_________个__________相乘.
a3表示_________个___________相乘.
(a2)3表示_________个__________相乘.
4
6
4
62
3
a
3
a2
15.1整式的乘法
学习目标:
1.理解幂的乘方的运算性质,进一步体会和巩固幂的意义;
2.掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
根据乘方的意义和同底数幂乘法填空:
(1)(32)3=32×32×32=3( )
(2) (a2)3=a2·a2·a2=a( )
(3)(am)3=am·am·am=a( )
6
6
3m
你认为(am)n等于什么
amn
你能对你的猜想给出验证吗
(am)n=am·am…am=am+m+…+m=amn
n个am
n个m
1、请你总结一下幂的乘方法则是什么?
幂的乘方,底数不变,指数相乘。
2、用字母表示幂的乘方法则:
(am)n=amn
学习目标一:理解幂的乘方的运算性质,进一步体会和巩固幂的意义.
例1:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.
例2:已知am=2,an=3,求a3m+2n的值
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
1、判断题:
(1)a5+a5=2a10 ( )
(2)(x3)3=x6 ( )
(3)(-3)2 (-3)4=36( )
(4)x3+y3=(x+y)3 ( )
×
×
√
×
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
2、若(x2)n=x8,则n=_______
4
3、若[(x3)m]2=x12,则m=_______
2
4、若xm x2m=2,求x9m的值.
8
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
5. ⑴试比较2100和375的大小
解:∵2100=(24)25=1625,
375=(33)25=2725
而16<27
∴2100<375
请根据上述解答过程比较:355
444 533的大小。
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
1、请你总结一下幂的乘方法则是什么?
幂的乘方,底数不变,指数相乘。
2、用字母表示幂的乘方法则:
(am)n=amn
1.(p7)4 2.m4·n+m·m3·n
3.(a4)3-(a3)4 4.26·2
5.105·10n+1 6.107·105·10n
7.[(a-b)m] n 8.(x2)3·x7
9.(x+y)7·(x+y)5 10.x2n·(xn)2
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
11.试比较2100和375的大小
解:∵2100=(24)25=1625,
375=(33)25=2725
而16<27
∴2100<375
请根据上述解答过程比较:355
444 533的大小。
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
1、叙述同底数幂乘法法则
同底数幂相乘底数不变,指数相加。
2、用字母表示同底数幂乘法法则
am·an=am+n
3、计算:①a2·a5·an;②a4·a4·a4
①a2+5+n
②a12
4.思考:
64表示_________个___________相乘.
(62)4表示_________个__________相乘.
a3表示_________个___________相乘.
(a2)3表示_________个__________相乘.
4
6
4
62
3
a
3
a2
15.1整式的乘法
学习目标:
1.理解幂的乘方的运算性质,进一步体会和巩固幂的意义;
2.掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
根据乘方的意义和同底数幂乘法填空:
(1)(32)3=32×32×32=3( )
(2) (a2)3=a2·a2·a2=a( )
(3)(am)3=am·am·am=a( )
6
6
3m
你认为(am)n等于什么
amn
你能对你的猜想给出验证吗
(am)n=am·am…am=am+m+…+m=amn
n个am
n个m
1、请你总结一下幂的乘方法则是什么?
幂的乘方,底数不变,指数相乘。
2、用字母表示幂的乘方法则:
(am)n=amn
学习目标一:理解幂的乘方的运算性质,进一步体会和巩固幂的意义.
例1:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.
例2:已知am=2,an=3,求a3m+2n的值
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
1、判断题:
(1)a5+a5=2a10 ( )
(2)(x3)3=x6 ( )
(3)(-3)2 (-3)4=36( )
(4)x3+y3=(x+y)3 ( )
×
×
√
×
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
2、若(x2)n=x8,则n=_______
4
3、若[(x3)m]2=x12,则m=_______
2
4、若xm x2m=2,求x9m的值.
8
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
5. ⑴试比较2100和375的大小
解:∵2100=(24)25=1625,
375=(33)25=2725
而16<27
∴2100<375
请根据上述解答过程比较:355
444 533的大小。
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
1、请你总结一下幂的乘方法则是什么?
幂的乘方,底数不变,指数相乘。
2、用字母表示幂的乘方法则:
(am)n=amn
1.(p7)4 2.m4·n+m·m3·n
3.(a4)3-(a3)4 4.26·2
5.105·10n+1 6.107·105·10n
7.[(a-b)m] n 8.(x2)3·x7
9.(x+y)7·(x+y)5 10.x2n·(xn)2
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
11.试比较2100和375的大小
解:∵2100=(24)25=1625,
375=(33)25=2725
而16<27
∴2100<375
请根据上述解答过程比较:355
444 533的大小。
学习目标二:掌握幂的乘方的运算性质,并灵活应用幂的乘方的性质.
