华东师大版(2012)七年级下册 8.2.2 不等式 的简单变形 课件(共20张PPT)
文档属性
| 名称 | 华东师大版(2012)七年级下册 8.2.2 不等式 的简单变形 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 317.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
8.2.2 不等式的简单变形
学习目标
1.通过探索合作,理解不等式的三条基本性质。
2.能根据不等式的性质判断问题。
3.经过对比分析掌握解不等式的基本方法。
4.重点区分解不等式时“系数化为1”与解方程的不同。
知识回顾
回忆:等式的基本性质有哪些?
等式的基本性质1:等式两边同时加上(或减去)同一个数或者同一个整式, 所得结果仍是等式.
即如果a=b,那么a+c=b+c,a-c=b-c
等式的基本性质2:等式两边同时乘以(或除以)同一个数(除数不能为0 ),所得结果仍是等式.
即如果a=b,那么ac=bc,
情境导入
问题情景:
你能准确填出不等号吗?
老师
学生
谁的年龄大?
30
13
三 年 前:
五 年 后:
30-3
13-3
30+5
13+5
>
>
>
______
______
______
假设:某老师今年a岁,某同学今年b岁, 如果已知老师与学生的年龄大小关系是:
C年前则有:
a>b
C年后则有:
a+c
b+c
__
>
a-c
b-c
__
>
探索合作
老师
学生
性质总结
结论:
如果a>b,那么:
a+c b+c, a-c b-c
这就是说,不等式的两边都 同一个数或同一个整式,不等号方向 。
不等式的性质1
不变
加上(或减去)
>
>
跟踪训练
一、根据“不等式的性质1”,请同学们试一试。
1、如果x>y,那么x+5 __ y+5,x-7__ y-7
>
2、如果3x<-2,那么3x+m___-2+m
3x-2x___-2-2x
3、如果a+10<b+10,那么a___b
4、如果a-4>b-4,那么a___b
<
>
<
<
>
对比分析
我们已经知道,解方程就是通过一系列变形,把方程变形为x=a的形式,与解方程一样,解不等式的过程,就是要将不等式变形成x>a 或x 这也就是不等式解集的
一般形式。
解:方程的两边都加上7,等式仍然成立,所以
例如: x -7=8
x -7<8
x-7+7=8+7
x-7+7 8+7
X<8+7
<
x=8+7
x=15
X<15
解:不等式的两边都加上7,不等号的方向不变,所以
“移项”
“移项”
性质运用
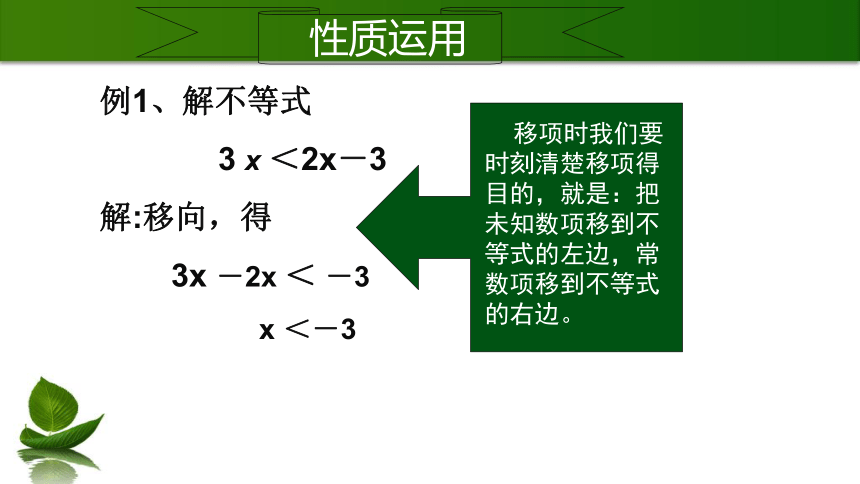
例1、解不等式
3 x <2x-3
解:移向,得
3x -2x < -3
x <-3
移项时我们要时刻清楚移项得目的,就是:把未知数项移到不等式的左边,常数项移到不等式的右边。
跟踪训练
二、解下列不等式。
将不等式7>4两边都乘以或除以同一个不为0的数,比较所得的数的大小,用“<”,“>”或“=”号填空:
7×3____4×3
7×2____4×2
7×1____4×1
7×0____4×0
7×(-1)___4×(-1)
7×(-2)___4×(-2)
7×(-3)___4×(-3)
………………………………………………
从中你能发现什么?
>
>
>
=
<
<
<
7÷3____4÷3
7÷2____4÷2
7÷1____4÷1
0不能做除数
7÷(-1)___4÷(-1)
7÷(-2)___4÷(-2)
7÷(-3)___4 × (-3)
<
<
<
>
>
>
试一试
性质总结
不等式性质2:
如果a >b,并且c>0,那么ac > bc, >
不等式性质3:
如果a >b,并且c<0,那么ac< bc, <
也就是说,不等式两边都____________ 同一个正数,不等号的方向_______;不等式两边都_____________同一个负数,不等号的方向________.
乘以(或除以)
不变
乘以(或除以)
改变
跟踪训练
三、根据“不等式的性质2、3”,请同学们试一试。
>
<
=
≥
≤
(1).如果a>b,c>0,那么ac bc。
(2).如果a>b,c<0,那么ac bc。
(3).如果a>b,c=0,那么ac bc。
(4).如果a>b,c≥0,那么ac bc。
(5).如果a>b,c≤0,那么ac bc。
对比分析
解:系数化为1,得
解:系数化为1,得
解:系数化为1,得
解:系数化为1,得
等式的基本性质2
不等式的基本性质2
不等式的基本性质3
一般情况下解方程的最后一步为“系数化为1”,解不等式也一样。
但它们的依据却大有不同。
>
>
>
>
<
<
方法总结
在解不等式“系数化为1”时,一定要看清未知数系数的正负。
(1)、当a>0时,系数化为1,得x>
ax>b
(2)、当a<0时,系数化为1,得x<
跟踪训练
四、解下列不等式。
>
<
五、选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得________,依据: .
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据_________________.
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
强化训练
自我反思
课本P57:
练 习 第1题
习题8.2 第1.3题
请同学们认真完成!!!
课后作业
再见
学习目标
1.通过探索合作,理解不等式的三条基本性质。
2.能根据不等式的性质判断问题。
3.经过对比分析掌握解不等式的基本方法。
4.重点区分解不等式时“系数化为1”与解方程的不同。
知识回顾
回忆:等式的基本性质有哪些?
等式的基本性质1:等式两边同时加上(或减去)同一个数或者同一个整式, 所得结果仍是等式.
即如果a=b,那么a+c=b+c,a-c=b-c
等式的基本性质2:等式两边同时乘以(或除以)同一个数(除数不能为0 ),所得结果仍是等式.
即如果a=b,那么ac=bc,
情境导入
问题情景:
你能准确填出不等号吗?
老师
学生
谁的年龄大?
30
13
三 年 前:
五 年 后:
30-3
13-3
30+5
13+5
>
>
>
______
______
______
假设:某老师今年a岁,某同学今年b岁, 如果已知老师与学生的年龄大小关系是:
C年前则有:
a>b
C年后则有:
a+c
b+c
__
>
a-c
b-c
__
>
探索合作
老师
学生
性质总结
结论:
如果a>b,那么:
a+c b+c, a-c b-c
这就是说,不等式的两边都 同一个数或同一个整式,不等号方向 。
不等式的性质1
不变
加上(或减去)
>
>
跟踪训练
一、根据“不等式的性质1”,请同学们试一试。
1、如果x>y,那么x+5 __ y+5,x-7__ y-7
>
2、如果3x<-2,那么3x+m___-2+m
3x-2x___-2-2x
3、如果a+10<b+10,那么a___b
4、如果a-4>b-4,那么a___b
<
>
<
<
>
对比分析
我们已经知道,解方程就是通过一系列变形,把方程变形为x=a的形式,与解方程一样,解不等式的过程,就是要将不等式变形成x>a 或x
一般形式。
解:方程的两边都加上7,等式仍然成立,所以
例如: x -7=8
x -7<8
x-7+7=8+7
x-7+7 8+7
X<8+7
<
x=8+7
x=15
X<15
解:不等式的两边都加上7,不等号的方向不变,所以
“移项”
“移项”
性质运用
例1、解不等式
3 x <2x-3
解:移向,得
3x -2x < -3
x <-3
移项时我们要时刻清楚移项得目的,就是:把未知数项移到不等式的左边,常数项移到不等式的右边。
跟踪训练
二、解下列不等式。
将不等式7>4两边都乘以或除以同一个不为0的数,比较所得的数的大小,用“<”,“>”或“=”号填空:
7×3____4×3
7×2____4×2
7×1____4×1
7×0____4×0
7×(-1)___4×(-1)
7×(-2)___4×(-2)
7×(-3)___4×(-3)
………………………………………………
从中你能发现什么?
>
>
>
=
<
<
<
7÷3____4÷3
7÷2____4÷2
7÷1____4÷1
0不能做除数
7÷(-1)___4÷(-1)
7÷(-2)___4÷(-2)
7÷(-3)___4 × (-3)
<
<
<
>
>
>
试一试
性质总结
不等式性质2:
如果a >b,并且c>0,那么ac > bc, >
不等式性质3:
如果a >b,并且c<0,那么ac< bc, <
也就是说,不等式两边都____________ 同一个正数,不等号的方向_______;不等式两边都_____________同一个负数,不等号的方向________.
乘以(或除以)
不变
乘以(或除以)
改变
跟踪训练
三、根据“不等式的性质2、3”,请同学们试一试。
>
<
=
≥
≤
(1).如果a>b,c>0,那么ac bc。
(2).如果a>b,c<0,那么ac bc。
(3).如果a>b,c=0,那么ac bc。
(4).如果a>b,c≥0,那么ac bc。
(5).如果a>b,c≤0,那么ac bc。
对比分析
解:系数化为1,得
解:系数化为1,得
解:系数化为1,得
解:系数化为1,得
等式的基本性质2
不等式的基本性质2
不等式的基本性质3
一般情况下解方程的最后一步为“系数化为1”,解不等式也一样。
但它们的依据却大有不同。
>
>
>
>
<
<
方法总结
在解不等式“系数化为1”时,一定要看清未知数系数的正负。
(1)、当a>0时,系数化为1,得x>
ax>b
(2)、当a<0时,系数化为1,得x<
跟踪训练
四、解下列不等式。
>
<
五、选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得________,依据: .
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据_________________.
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
强化训练
自我反思
课本P57:
练 习 第1题
习题8.2 第1.3题
请同学们认真完成!!!
课后作业
再见
