华东师大版八年级数学(下册)课件:17.1.2函数及其图象(共15张PPT)
文档属性
| 名称 | 华东师大版八年级数学(下册)课件:17.1.2函数及其图象(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 659.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




文档简介
*
一课时
华东师大版八年级(下册)
*
1.购买单价为每本10元的书籍,付款总金额y(元),购买本数x(本).
问:函数关系式为_____________.变量是____,常量是__ __,
_____是自变量, ______是因变量,______是_____的函数.
2.半径为R的球, 体积为V,则V与R的函数关系式为 ,
自变量是_____, ____是_____的函数.
? R?
V=
3
4
做一做
一般地,在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称y是x的函数.
复习:什么叫函数?
函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
y=10x
(x≥0)
x
y
x
x
y
y
10
R
R
V
*
注意:判断是不是函数,我们可以看它的数学式子中的变量之间是
否满足函数的定义.
例1.判断下列变量关系是不是函数?
(1)长方形面积S=ab.
(2)关系式y=± 中,y是x的函数吗?
x
不是
不是
出现三个变量
变量间不是唯一关系
思考:什么叫函数关系式?
用来表示函数关系的等式叫做函数关系式,
f =
300000
?
C=2? r
也称为函数的解析式.
函数的关系式是等式.
通常等式的右边是含有自变量的代数式,左边的一个字母表示函数.
试一试:矩形的周长是18cm,它的长是ycm,宽是xcm.写出y与x的函数
关系式
(9>x≥0)
*
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
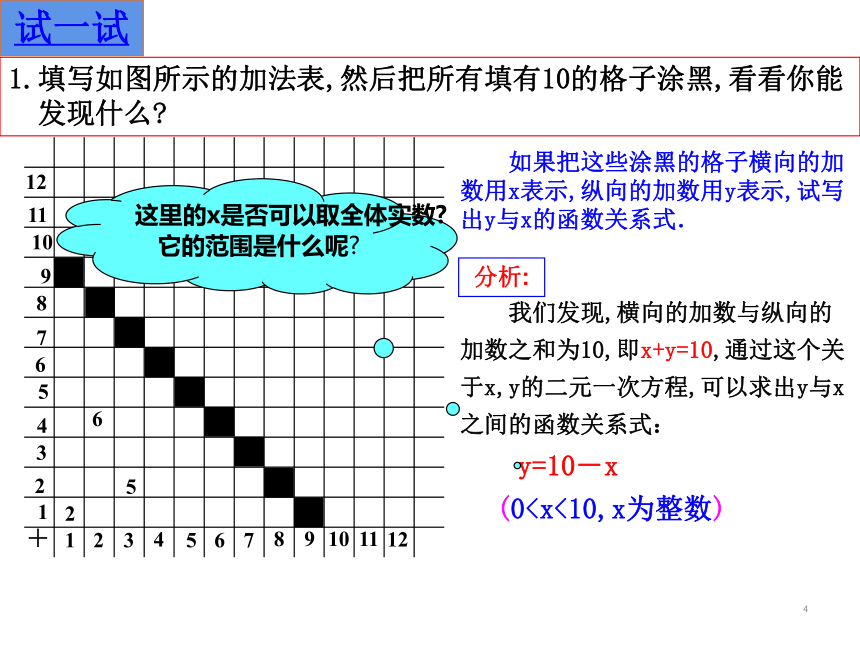
1.填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能
发现什么?
试一试
如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.
我们发现,横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式:
分析:
y=10-x
(0 这里的x是否可以取全体实数?它的范围是什么呢?
*
x
y
A
M
y= x?
1
2
(0 ≤ x≤10 )
A
B
C
P
Q
M
N
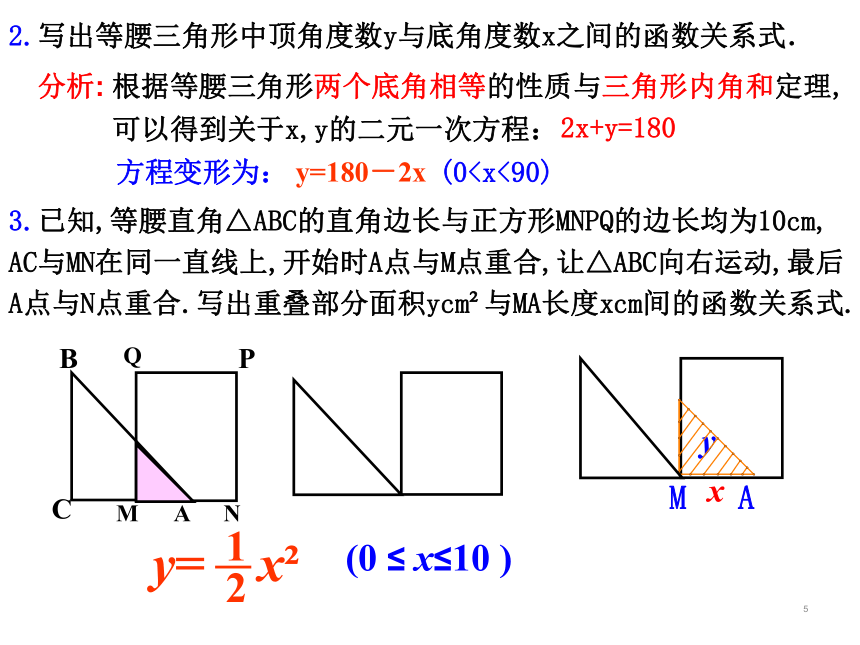
3.已知,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,
AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.写出重叠部分面积ycm?与MA长度xcm间的函数关系式.
2.写出等腰三角形中顶角度数y与底角度数x之间的函数关系式.
根据等腰三角形两个底角相等的性质与三角形内角和定理,
可以得到关于x,y的二元一次方程:
分析:
方程变形为:
y=180-2x
(02x+y=180
*
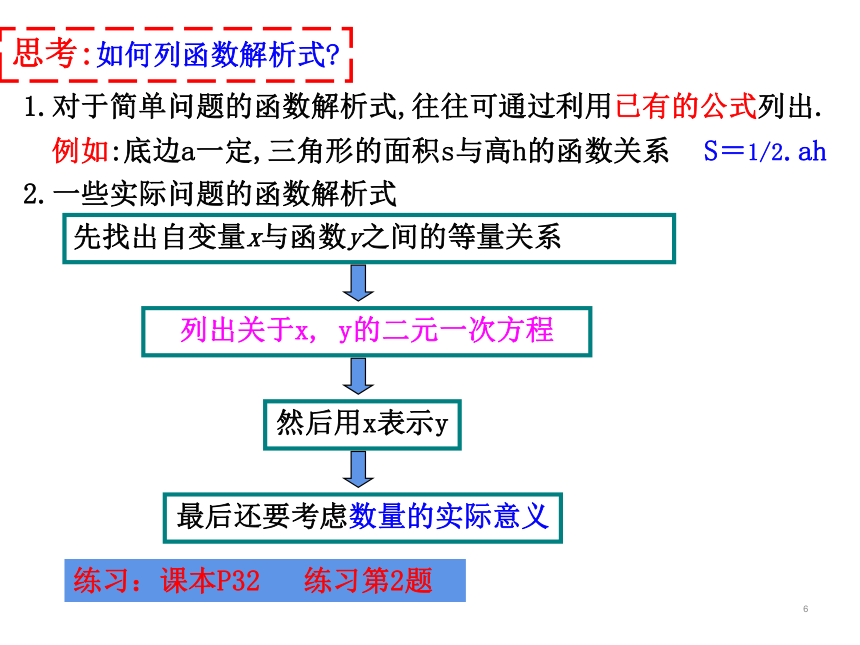
思考:如何列函数解析式?
1.对于简单问题的函数解析式,往往可通过利用已有的公式列出.
2.一些实际问题的函数解析式
例如:底边a一定,三角形的面积s与高h的函数关系
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
S=1/2.ah
练习:课本P32 练习第2题
*
如何理解自变量的取值范围?
y=10-x
(0y=180°-2x
(0(0 ≤ x≤10 )
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
例2 .求下列函数中自变量x的取值范围
1) y = 3x-1 ; 2) y =2x?+7 ; 3) y = ; 4) y= .
y= x?
分析:用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值。
(4) x≥2 .
(1) x取任意实数;
(2) x取任意实数;
(3) x≠-2
解:
*
1.当函数解析式是一个整式时,自变量的取值范围是
2.当函数解析式是分式时,自变量的取值范围是
3.当函数解析式是二次根式时,自变量的取值范围是
一.函数解析式是数学式子的自变量取值范围:
全体实数.
使分母不为零的实数.
使被开方数不小于零的数
归纳
*
二.实际问题的函数解析式中自变量取值范围:
函数自变量的取值范围既要使实际问题有意义,同时又要使解析式有意义.
2.实际问题有意义主要指的是:
(1)取值符合问题的实际背景.
(2)取值保证几何图形存在.
(例如自变量表示人数时,应为非负整数等)
(例如等腰三角形底角大于0度小于90度等).
*
练习:求下列函数中自变量x的取值范围:
y = 3x+2 ;
(2)y =-5x? ;
y = ;
(4)y = .
x-2
3
x-4
(1) x取全体实数;
(2) x取全体实数;
(3) x ≠ 2;
(4) x≥4 .
*
练习:
例3.求下列函数中自变量x的取值范围
∴x≥1且x≠2
x-1≥0
x-2≠0
(1)根据题意可得
x≥1
x≠ 2
解得
解:
x+3>0
3-x≥ 0
(2)根据题意可得
解得
x>-3
x≤ 3
∴ 3≥x>-3
*
例4.在课本32页例2问题(2)中,当MA=1 cm时,重叠部分的面积
是多少?
解
(1)设重叠部分面积为ycm?,MA长为x cm,则
y与x之间的函数关系式为:
(0 ≤ x≤10 )
(2)当x=1时,
注意:y=
1
2
叫做当x=1时的函数值.
练习:课本P32 练习第1题
*
小 结
1.函数关系式
用来表示函数关系的等式叫做函数关系式,也称为函数的解析式.
2.列函数解析式的方法
3.函数自变量的取值范围:
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
4 求自变量取值范围的方法:
根据使函数表示的实际问题有意义的条件,以及使函数解析式中的数学式子有意义的条件,列出不等式或不等式组,求出它或它们的解集,即为自变量的取值范围.
*
课本P33 第2、3、4题
*
一课时
华东师大版八年级(下册)
*
1.购买单价为每本10元的书籍,付款总金额y(元),购买本数x(本).
问:函数关系式为_____________.变量是____,常量是__ __,
_____是自变量, ______是因变量,______是_____的函数.
2.半径为R的球, 体积为V,则V与R的函数关系式为 ,
自变量是_____, ____是_____的函数.
? R?
V=
3
4
做一做
一般地,在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称y是x的函数.
复习:什么叫函数?
函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
y=10x
(x≥0)
x
y
x
x
y
y
10
R
R
V
*
注意:判断是不是函数,我们可以看它的数学式子中的变量之间是
否满足函数的定义.
例1.判断下列变量关系是不是函数?
(1)长方形面积S=ab.
(2)关系式y=± 中,y是x的函数吗?
x
不是
不是
出现三个变量
变量间不是唯一关系
思考:什么叫函数关系式?
用来表示函数关系的等式叫做函数关系式,
f =
300000
?
C=2? r
也称为函数的解析式.
函数的关系式是等式.
通常等式的右边是含有自变量的代数式,左边的一个字母表示函数.
试一试:矩形的周长是18cm,它的长是ycm,宽是xcm.写出y与x的函数
关系式
(9>x≥0)
*
1
1
2
3
4
5
6
7
12
8
10
11
9
2
3
4
5
6
7
12
8
10
11
9
5
6
2
+
1.填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能
发现什么?
试一试
如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.
我们发现,横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式:
分析:
y=10-x
(0
*
x
y
A
M
y= x?
1
2
(0 ≤ x≤10 )
A
B
C
P
Q
M
N
3.已知,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,
AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.写出重叠部分面积ycm?与MA长度xcm间的函数关系式.
2.写出等腰三角形中顶角度数y与底角度数x之间的函数关系式.
根据等腰三角形两个底角相等的性质与三角形内角和定理,
可以得到关于x,y的二元一次方程:
分析:
方程变形为:
y=180-2x
(0
*
思考:如何列函数解析式?
1.对于简单问题的函数解析式,往往可通过利用已有的公式列出.
2.一些实际问题的函数解析式
例如:底边a一定,三角形的面积s与高h的函数关系
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
然后用x表示y
最后还要考虑数量的实际意义
S=1/2.ah
练习:课本P32 练习第2题
*
如何理解自变量的取值范围?
y=10-x
(0
(0
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
例2 .求下列函数中自变量x的取值范围
1) y = 3x-1 ; 2) y =2x?+7 ; 3) y = ; 4) y= .
y= x?
分析:用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值。
(4) x≥2 .
(1) x取任意实数;
(2) x取任意实数;
(3) x≠-2
解:
*
1.当函数解析式是一个整式时,自变量的取值范围是
2.当函数解析式是分式时,自变量的取值范围是
3.当函数解析式是二次根式时,自变量的取值范围是
一.函数解析式是数学式子的自变量取值范围:
全体实数.
使分母不为零的实数.
使被开方数不小于零的数
归纳
*
二.实际问题的函数解析式中自变量取值范围:
函数自变量的取值范围既要使实际问题有意义,同时又要使解析式有意义.
2.实际问题有意义主要指的是:
(1)取值符合问题的实际背景.
(2)取值保证几何图形存在.
(例如自变量表示人数时,应为非负整数等)
(例如等腰三角形底角大于0度小于90度等).
*
练习:求下列函数中自变量x的取值范围:
y = 3x+2 ;
(2)y =-5x? ;
y = ;
(4)y = .
x-2
3
x-4
(1) x取全体实数;
(2) x取全体实数;
(3) x ≠ 2;
(4) x≥4 .
*
练习:
例3.求下列函数中自变量x的取值范围
∴x≥1且x≠2
x-1≥0
x-2≠0
(1)根据题意可得
x≥1
x≠ 2
解得
解:
x+3>0
3-x≥ 0
(2)根据题意可得
解得
x>-3
x≤ 3
∴ 3≥x>-3
*
例4.在课本32页例2问题(2)中,当MA=1 cm时,重叠部分的面积
是多少?
解
(1)设重叠部分面积为ycm?,MA长为x cm,则
y与x之间的函数关系式为:
(0 ≤ x≤10 )
(2)当x=1时,
注意:y=
1
2
叫做当x=1时的函数值.
练习:课本P32 练习第1题
*
小 结
1.函数关系式
用来表示函数关系的等式叫做函数关系式,也称为函数的解析式.
2.列函数解析式的方法
3.函数自变量的取值范围:
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
4 求自变量取值范围的方法:
根据使函数表示的实际问题有意义的条件,以及使函数解析式中的数学式子有意义的条件,列出不等式或不等式组,求出它或它们的解集,即为自变量的取值范围.
*
课本P33 第2、3、4题
*
