华东师大版八年级下册 17.2 . 1平面直角坐标系课件(共39张PPT)
文档属性
| 名称 | 华东师大版八年级下册 17.2 . 1平面直角坐标系课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 13.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 13:49:44 | ||
图片预览










文档简介
华东师大版八年级(下册)
第17章 函数及其图象
17.2 函数的图象(第1课时)
1.平面直角坐标系
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,也叫笛卡尔坐标系.
概念学习
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
水平方向的数轴称为x轴或横轴,垂直方向的数轴称为y轴或纵轴,它们称为坐标轴.两轴交点O称为原点.
问题1:如何表示在平面直角坐标系中的点呢?
同学,你知道自己的座位号吗?
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
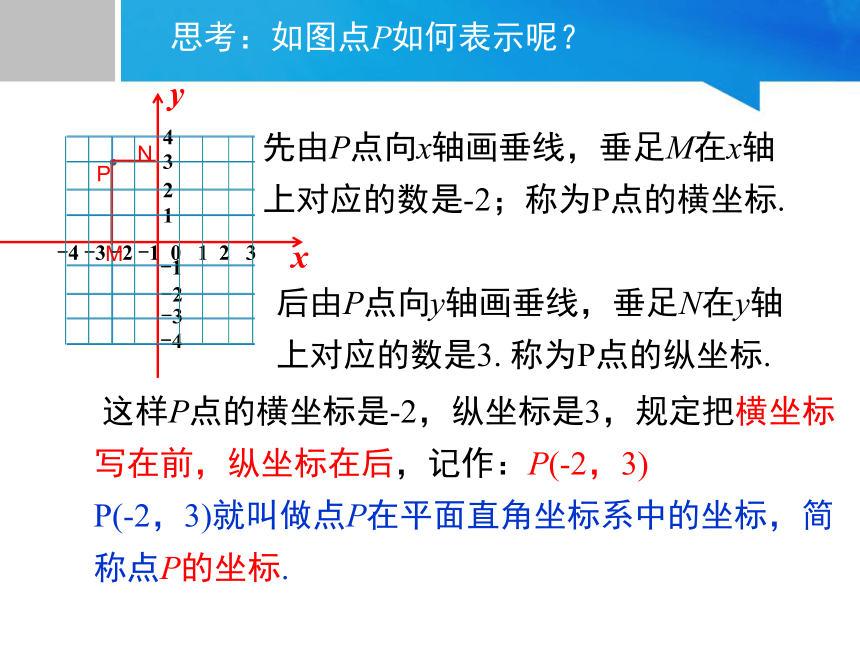
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上对应的数是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上对应的数是-2;称为P点的横坐标.
P
N
M
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
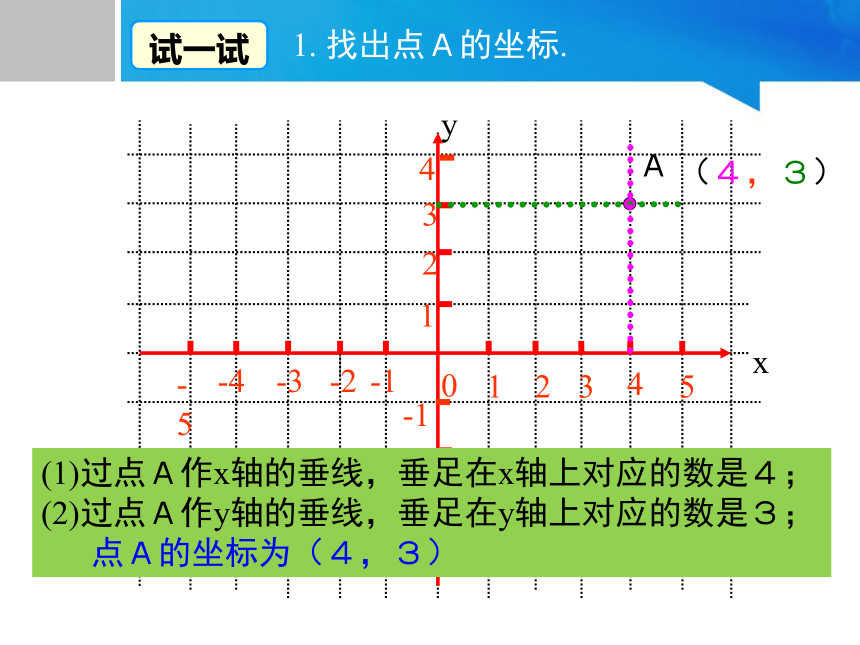
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
问题2:如何在平面直角坐标系中找到某一点的位置呢?
小明父子俩周末去电影院看电影,买了两张票,座位号分别是3排6号和6排3号.怎样才能既快又准地找到座位?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
思考1 在班里老师想找一个学生,你知道是谁吗?
思考2 你认为确定一个位置需要几个数据?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
总结:平面直角坐标系中的点都有一个坐标;每一个坐标都表示在坐标系中的某个点。
结论:平面直角坐标系中的点和有序实数对 一一对应
问题3:(3,6)与(6,3)是同一个点吗?
强调:1.有序,先横后纵;
2.表示坐标要有括号,并用逗号隔开.
典例精析
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
A
B
C
E
F
D
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
y
O
x
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
例2: 在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
练一练
游戏活动
找一位同学作为坐标原点,伸出两只手臂作为坐标轴,手指的方向为正方向。其他同学写出自己的坐标。
直角坐标系中点的坐标的特征
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
巩固练习
1:在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),
C (-4 ,-1),D(2,-4).
2.已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组
解得m>2.
m>2
【方法总结】求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
3. 点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
【方法总结】坐标轴上的点的坐标特点:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值,进而求出点的坐标.
问题7:在我们的现实生活中除了我们今天的平面直角坐标系来确定点的位置,还有那些也可以用来确定点的位置呢?
如:经纬坐标,极坐标,棋盘坐标等。
(1)如图2,所示的国际象棋的棋盘中,双方四只马的位置分别是A(b,3)、B(d、5)、C(f,7)、D(h,2),请在图中描出它们的位置.(课本练习3)
(2)如图3,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横线用数字表示,纵线用英文字母表示,这样,黑棋①的由置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为_________。
平面直角坐标系
定义:原点、坐标轴
课堂小结
点的坐标
定义与符号特征
点的坐标的确定
解析几何的诞生—数学中的转折点
笛卡儿
(法,1596-1650年)
法国科学家、哲学家和数学家
1616年获法学博士学位,1618-1621年投笔从戎,1628年移居荷兰,1649年到斯德哥尔摩
欧洲近代哲学的奠基人之一,17世纪欧洲哲学界和科学界最有影响的巨匠之一
“近代科学的始祖”“解析几何之父”
任何问题?数学问题?代数问题?方程求解
“我思故我在”
笛卡儿,欧洲文艺复兴以来,第一个为人类争取并保证理性权利的人。
课后拓展:每位同学收集至少五名数学家的事迹,用小卡片记载下来,大家交流学习。
谢谢大家!
第17章 函数及其图象
17.2 函数的图象(第1课时)
1.平面直角坐标系
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,也叫笛卡尔坐标系.
概念学习
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
水平方向的数轴称为x轴或横轴,垂直方向的数轴称为y轴或纵轴,它们称为坐标轴.两轴交点O称为原点.
问题1:如何表示在平面直角坐标系中的点呢?
同学,你知道自己的座位号吗?
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上对应的数是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上对应的数是-2;称为P点的横坐标.
P
N
M
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
问题2:如何在平面直角坐标系中找到某一点的位置呢?
小明父子俩周末去电影院看电影,买了两张票,座位号分别是3排6号和6排3号.怎样才能既快又准地找到座位?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
思考1 在班里老师想找一个学生,你知道是谁吗?
思考2 你认为确定一个位置需要几个数据?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
总结:平面直角坐标系中的点都有一个坐标;每一个坐标都表示在坐标系中的某个点。
结论:平面直角坐标系中的点和有序实数对 一一对应
问题3:(3,6)与(6,3)是同一个点吗?
强调:1.有序,先横后纵;
2.表示坐标要有括号,并用逗号隔开.
典例精析
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
A
B
C
E
F
D
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
y
O
x
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
例2: 在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
练一练
游戏活动
找一位同学作为坐标原点,伸出两只手臂作为坐标轴,手指的方向为正方向。其他同学写出自己的坐标。
直角坐标系中点的坐标的特征
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
巩固练习
1:在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),
C (-4 ,-1),D(2,-4).
2.已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组
解得m>2.
m>2
【方法总结】求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
3. 点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
【方法总结】坐标轴上的点的坐标特点:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值,进而求出点的坐标.
问题7:在我们的现实生活中除了我们今天的平面直角坐标系来确定点的位置,还有那些也可以用来确定点的位置呢?
如:经纬坐标,极坐标,棋盘坐标等。
(1)如图2,所示的国际象棋的棋盘中,双方四只马的位置分别是A(b,3)、B(d、5)、C(f,7)、D(h,2),请在图中描出它们的位置.(课本练习3)
(2)如图3,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横线用数字表示,纵线用英文字母表示,这样,黑棋①的由置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为_________。
平面直角坐标系
定义:原点、坐标轴
课堂小结
点的坐标
定义与符号特征
点的坐标的确定
解析几何的诞生—数学中的转折点
笛卡儿
(法,1596-1650年)
法国科学家、哲学家和数学家
1616年获法学博士学位,1618-1621年投笔从戎,1628年移居荷兰,1649年到斯德哥尔摩
欧洲近代哲学的奠基人之一,17世纪欧洲哲学界和科学界最有影响的巨匠之一
“近代科学的始祖”“解析几何之父”
任何问题?数学问题?代数问题?方程求解
“我思故我在”
笛卡儿,欧洲文艺复兴以来,第一个为人类争取并保证理性权利的人。
课后拓展:每位同学收集至少五名数学家的事迹,用小卡片记载下来,大家交流学习。
谢谢大家!
