华东师大版八年级下册17.5.1实践和探索(1)课件(18张PPT)
文档属性
| 名称 | 华东师大版八年级下册17.5.1实践和探索(1)课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 16:01:13 | ||
图片预览




文档简介
八年级数学(下)第十七章函数及其图象
17.5.1实践与探索
一次函数图像的交点
1.理解二元一次方程组的解是两直线的交点坐标。
2.能通过图像法求出二元一次方程组的解;培养分析问题、解决问题和类比、归纳的能力。
重点:利用图像法求出二元一次方程组的解。
难点:一次函数与二元一次方程组的关系。
?
?
学习目标
情境导入
0 2 4 6 8 10 12 14 16 18 20
1200
1080
960
840
720
600
480
360
240
120
B
A
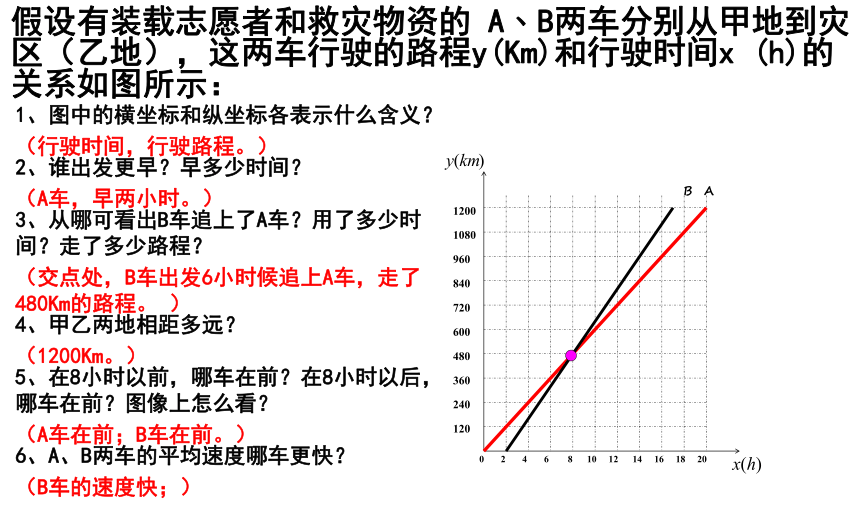
1、图中的横坐标和纵坐标各表示什么含义?
2、谁出发更早?早多少时间?
3、从哪可看出B车追上了A车?用了多少时间?走了多少路程?
4、甲乙两地相距多远?
5、在8小时以前,哪车在前?在8小时以后,哪车在前?图像上怎么看?
6、A、B两车的平均速度哪车更快?
(行驶时间,行驶路程。)
(A车,早两小时。)
(交点处,B车出发6小时候追上A车,走了480Km的路程。 )
(1200Km。)
(A车在前;B车在前。)
(B车的速度快;)
假设有装载志愿者和救灾物资的 A﹑B两车分别从甲地到灾
区(乙地),这两车行驶的路程y(Km)和行驶时间x (h)的
关系如图所示:
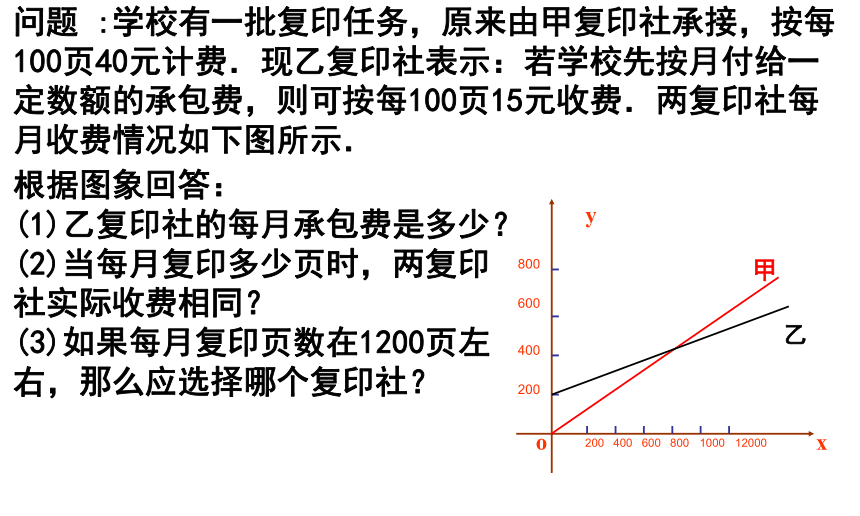
问题 :学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如下图所示.
根据图象回答:
(1)乙复印社的每月承包费是多少?
(2)当每月复印多少页时,两复印社实际收费相同?
(3)如果每月复印页数在1200页左右,那么应选择哪个复印社?
o
800
600
200
400
400
200
600
800
1000
12000
x
y
甲
乙
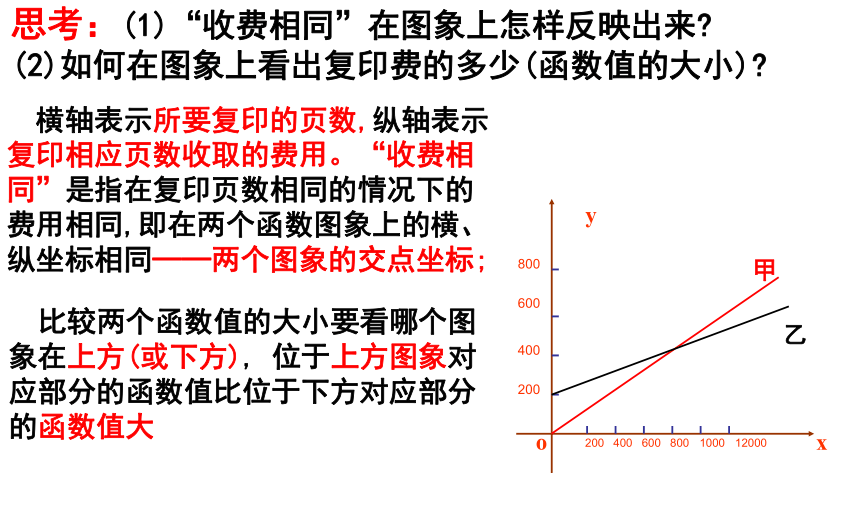
思考:(1)“收费相同”在图象上怎样反映出来?
(2)如何在图象上看出复印费的多少(函数值的大小)?
o
800
600
200
400
400
200
600
800
1000
12000
x
y
横轴表示所要复印的页数,纵轴表示复印相应页数收取的费用。“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象上的横、纵坐标相同──两个图象的交点坐标;
比较两个函数值的大小要看哪个图象在上方(或下方), 位于上方图象对应部分的函数值比位于下方对应部分的函数值大
甲
乙
归纳:由函数图象解答问题时,首先要明确横、纵轴表示的含义, 函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位 于上方图象的函数值要比位于下方图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确, 观察得越仔 细,所得的值就越准确.
④如果每月复印页数在1200页左右,那么应选择哪个复印社? 800页呢?500页呢?
·
> 800
< 800
y= 0.4x
y= 0.15x+200
①求两函数关系式
y= 0.4x
y= 0.15x+200
③从图象中可知当x_________时, 的?
从图象中可知当x_________时, 的?
x=800,
y=320
当x=1200,选择乙复印社合算;x=500,选择甲复印社合算;x=800,选择甲乙复印社费用一样
解: 在直角坐标系中画出两条直线,如下图所示.
o
y
x
两条直线的交点坐标是( -4 , 1 ),
所以方程组的解为
y=x+5
1、要求方程组 的解,需求直线 和直线 的交点坐标
2、直线2x-y=2 和 x+y=-5的交点坐标是 (-1,-4)
则 的解是 。
1
o
2
3
10
20
30
25
甲
乙
t /h
y/cm
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(㎝)与燃烧时间x (h)之间的关系如图所示。请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是_____________
从点燃到燃尽所用的时间分别是___________.
30cm、25cm
2h、2.5h
1
o
2
3
10
20
30
25
甲
乙
t /h
y/cm
(2)分别求甲、乙两根蜡烛燃烧时y与x之
间的函数关系式;
(3)燃烧多长时间时,甲乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?
做一做:下图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)问快艇出发多长时间赶上轮船?
解 (1)设表示轮船行驶过程的函数解析式为y=kx(k≠0),
由图象知:当x=8时,y=160.
代入上式,得8k=160, 可解得k=20.
所以轮船行驶过程的函数解析式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b(a≠0),
由图象知:当x=2时,y=0;当x=6时,y=160.
代入上式,得
可解得
所以快艇行驶过程的函数解析式为y=40x-80.
(2)由图象可知,轮船在8小时内行驶了160千米,快艇在4小时内行驶了160千米,所以轮船的速度是 ( 千米/时)
(3)设轮船出发x小时快艇赶上轮船,
20x=40x-80
得x=4,x-2=2.
答 快艇出发了2小时赶上轮船.
快艇的速度是 (千米/时).
一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数图象的交点(即是两条直线的交点).两个一次函数图象的交点坐标(即两条直线的交点),可以看成是某个二元一次方程组的解.
2、二元一次方程组的解与一次函数图像交点的关系:
课堂小结
1、从图像中获取信息,关键看图形中的以下几点:
1)两坐标轴的含义; 2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.
我们的生活离不开数学,我们要做生活的有心人。
17.5.1实践与探索
一次函数图像的交点
1.理解二元一次方程组的解是两直线的交点坐标。
2.能通过图像法求出二元一次方程组的解;培养分析问题、解决问题和类比、归纳的能力。
重点:利用图像法求出二元一次方程组的解。
难点:一次函数与二元一次方程组的关系。
?
?
学习目标
情境导入
0 2 4 6 8 10 12 14 16 18 20
1200
1080
960
840
720
600
480
360
240
120
B
A
1、图中的横坐标和纵坐标各表示什么含义?
2、谁出发更早?早多少时间?
3、从哪可看出B车追上了A车?用了多少时间?走了多少路程?
4、甲乙两地相距多远?
5、在8小时以前,哪车在前?在8小时以后,哪车在前?图像上怎么看?
6、A、B两车的平均速度哪车更快?
(行驶时间,行驶路程。)
(A车,早两小时。)
(交点处,B车出发6小时候追上A车,走了480Km的路程。 )
(1200Km。)
(A车在前;B车在前。)
(B车的速度快;)
假设有装载志愿者和救灾物资的 A﹑B两车分别从甲地到灾
区(乙地),这两车行驶的路程y(Km)和行驶时间x (h)的
关系如图所示:
问题 :学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如下图所示.
根据图象回答:
(1)乙复印社的每月承包费是多少?
(2)当每月复印多少页时,两复印社实际收费相同?
(3)如果每月复印页数在1200页左右,那么应选择哪个复印社?
o
800
600
200
400
400
200
600
800
1000
12000
x
y
甲
乙
思考:(1)“收费相同”在图象上怎样反映出来?
(2)如何在图象上看出复印费的多少(函数值的大小)?
o
800
600
200
400
400
200
600
800
1000
12000
x
y
横轴表示所要复印的页数,纵轴表示复印相应页数收取的费用。“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象上的横、纵坐标相同──两个图象的交点坐标;
比较两个函数值的大小要看哪个图象在上方(或下方), 位于上方图象对应部分的函数值比位于下方对应部分的函数值大
甲
乙
归纳:由函数图象解答问题时,首先要明确横、纵轴表示的含义, 函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位 于上方图象的函数值要比位于下方图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确, 观察得越仔 细,所得的值就越准确.
④如果每月复印页数在1200页左右,那么应选择哪个复印社? 800页呢?500页呢?
·
> 800
< 800
y= 0.4x
y= 0.15x+200
①求两函数关系式
y= 0.4x
y= 0.15x+200
③从图象中可知当x_________时, 的?
从图象中可知当x_________时, 的?
x=800,
y=320
当x=1200,选择乙复印社合算;x=500,选择甲复印社合算;x=800,选择甲乙复印社费用一样
解: 在直角坐标系中画出两条直线,如下图所示.
o
y
x
两条直线的交点坐标是( -4 , 1 ),
所以方程组的解为
y=x+5
1、要求方程组 的解,需求直线 和直线 的交点坐标
2、直线2x-y=2 和 x+y=-5的交点坐标是 (-1,-4)
则 的解是 。
1
o
2
3
10
20
30
25
甲
乙
t /h
y/cm
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(㎝)与燃烧时间x (h)之间的关系如图所示。请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是_____________
从点燃到燃尽所用的时间分别是___________.
30cm、25cm
2h、2.5h
1
o
2
3
10
20
30
25
甲
乙
t /h
y/cm
(2)分别求甲、乙两根蜡烛燃烧时y与x之
间的函数关系式;
(3)燃烧多长时间时,甲乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?
做一做:下图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)问快艇出发多长时间赶上轮船?
解 (1)设表示轮船行驶过程的函数解析式为y=kx(k≠0),
由图象知:当x=8时,y=160.
代入上式,得8k=160, 可解得k=20.
所以轮船行驶过程的函数解析式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b(a≠0),
由图象知:当x=2时,y=0;当x=6时,y=160.
代入上式,得
可解得
所以快艇行驶过程的函数解析式为y=40x-80.
(2)由图象可知,轮船在8小时内行驶了160千米,快艇在4小时内行驶了160千米,所以轮船的速度是 ( 千米/时)
(3)设轮船出发x小时快艇赶上轮船,
20x=40x-80
得x=4,x-2=2.
答 快艇出发了2小时赶上轮船.
快艇的速度是 (千米/时).
一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数图象的交点(即是两条直线的交点).两个一次函数图象的交点坐标(即两条直线的交点),可以看成是某个二元一次方程组的解.
2、二元一次方程组的解与一次函数图像交点的关系:
课堂小结
1、从图像中获取信息,关键看图形中的以下几点:
1)两坐标轴的含义; 2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.
我们的生活离不开数学,我们要做生活的有心人。
