华东师大版八年级下册18.1平行四边形对角线的性质课件(共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.1平行四边形对角线的性质课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 792.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览



文档简介
18.1 平行四边形的性质
第十八章 平行四边形
第3课时 平行四边形对角线的特征
教学目标:
1.探索并掌握平行四边形对角线的性质;
2.灵活运用平行四边形对角线的性质进行推
理和计算
教学重难点:
平行四边形对角线性质的推理
一、回顾与复习
用文字和几何语言叙述平行四边形的性质
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
A
B
D
C
O
AB=CD;AD=BC
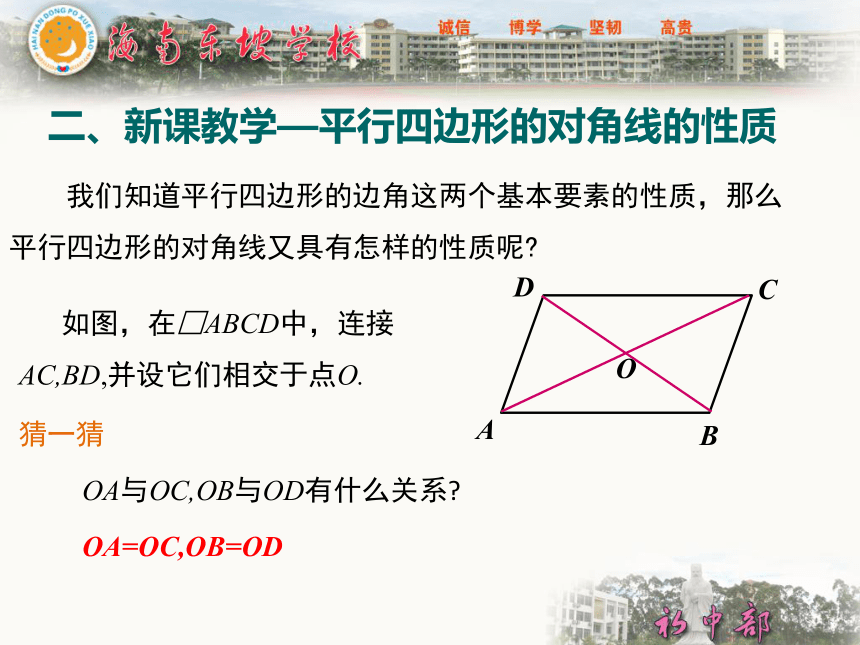
二、新课教学—平行四边形的对角线的性质
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
A
B
C
D
O
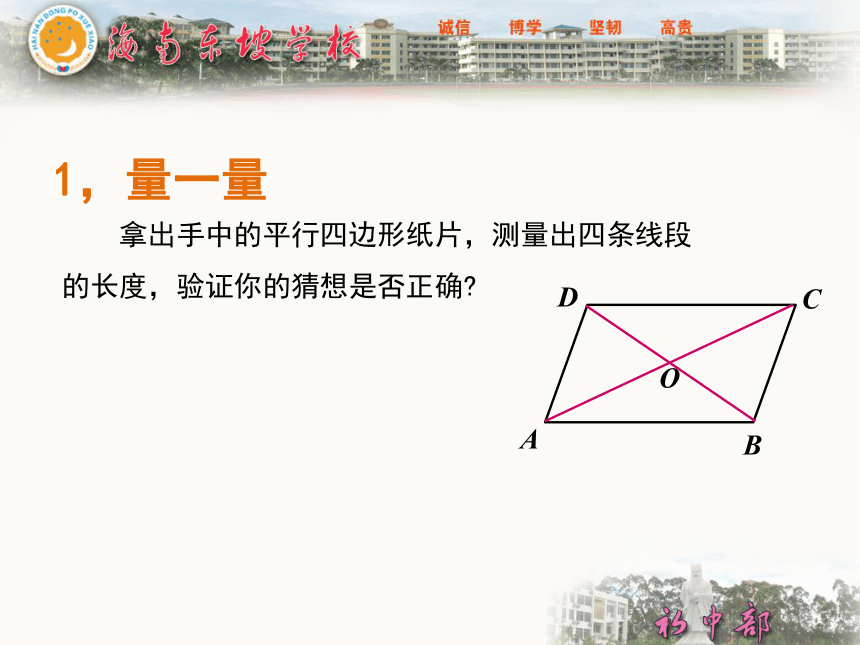
1,量一量
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确?
A
B
D
C
O
A
B
D
C
O
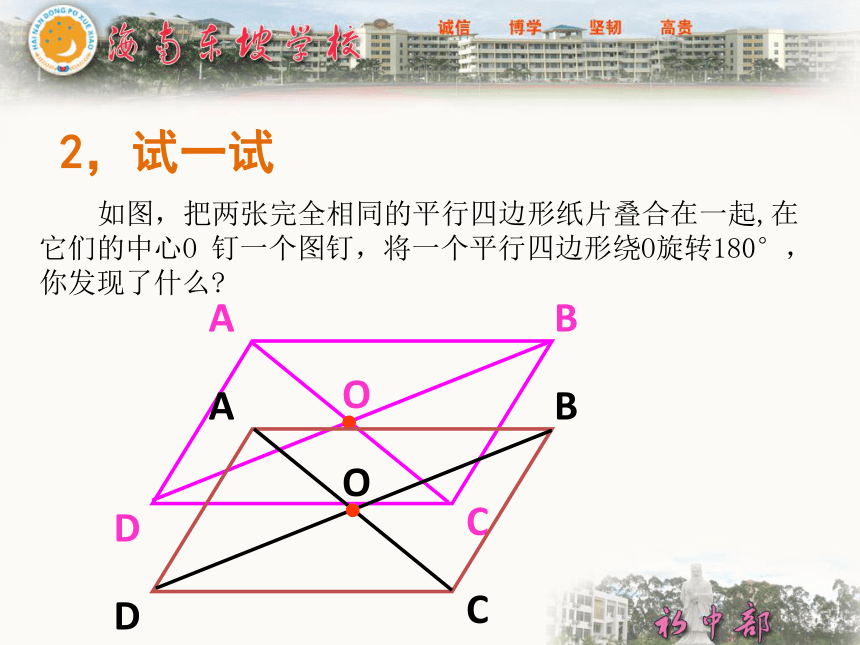
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
2,试一试
●
A
D
O
C
B
D
B
O
C
A
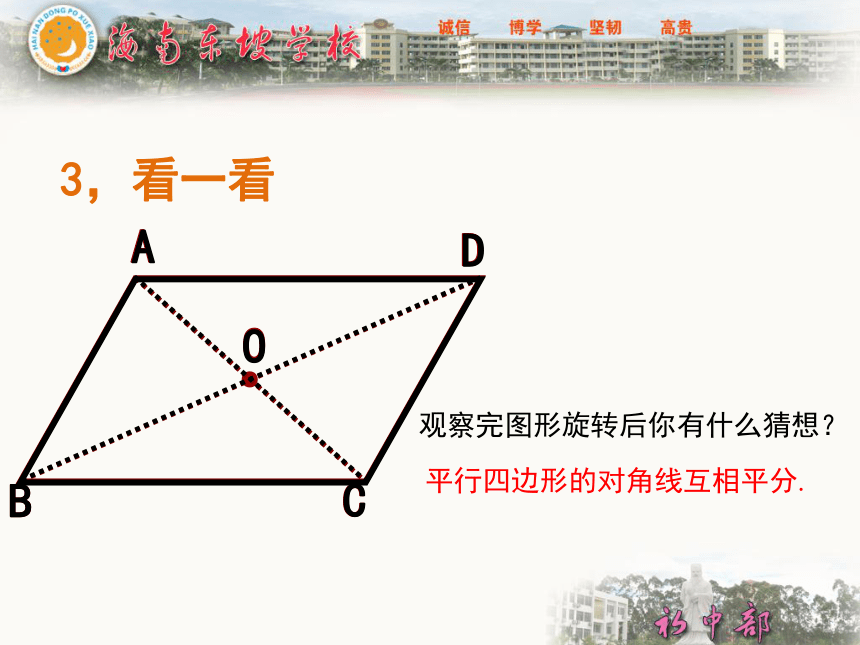
观察完图形旋转后你有什么猜想?
平行四边形的对角线互相平分.
3,看一看
4,证一证
已知:如图: □ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
A
C
D
B
O
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
归纳总结
例 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:
∵四边形ABCD是平行四边形
∴BC=AD=5
∴AB⊥AC
∴△ABC是直角三角形
AO= AC=2
∴BD=2BO=
典例精析
∴BO=
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
4
7
3
练一练
第十九章 四边形
2.已知: □ ABCD的对角线AC、BD相交于点
O,AC =16㎝,BD =12㎝,BC =10㎝,
则□ABCD 的周长是_______,
□ ABCD的面积是__________。
40cm
96cm2
8
6
10
10
练一练
八年级 数学
第十九章 四边形
练一练
1、 通过本节课的学习,你有什么收获?
2、 平行四边形的性质有哪些?
课堂小结
第十八章 平行四边形
第3课时 平行四边形对角线的特征
教学目标:
1.探索并掌握平行四边形对角线的性质;
2.灵活运用平行四边形对角线的性质进行推
理和计算
教学重难点:
平行四边形对角线性质的推理
一、回顾与复习
用文字和几何语言叙述平行四边形的性质
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
A
B
D
C
O
AB=CD;AD=BC
二、新课教学—平行四边形的对角线的性质
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
A
B
C
D
O
1,量一量
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确?
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
2,试一试
●
A
D
O
C
B
D
B
O
C
A
观察完图形旋转后你有什么猜想?
平行四边形的对角线互相平分.
3,看一看
4,证一证
已知:如图: □ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
A
C
D
B
O
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
归纳总结
例 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:
∵四边形ABCD是平行四边形
∴BC=AD=5
∴AB⊥AC
∴△ABC是直角三角形
AO= AC=2
∴BD=2BO=
典例精析
∴BO=
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
4
7
3
练一练
第十九章 四边形
2.已知: □ ABCD的对角线AC、BD相交于点
O,AC =16㎝,BD =12㎝,BC =10㎝,
则□ABCD 的周长是_______,
□ ABCD的面积是__________。
40cm
96cm2
8
6
10
10
练一练
八年级 数学
第十九章 四边形
练一练
1、 通过本节课的学习,你有什么收获?
2、 平行四边形的性质有哪些?
课堂小结
