华东师大版八年级下册18.2.1平行四边形的判定(1)课件(22张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.2.1平行四边形的判定(1)课件(22张PPT) | 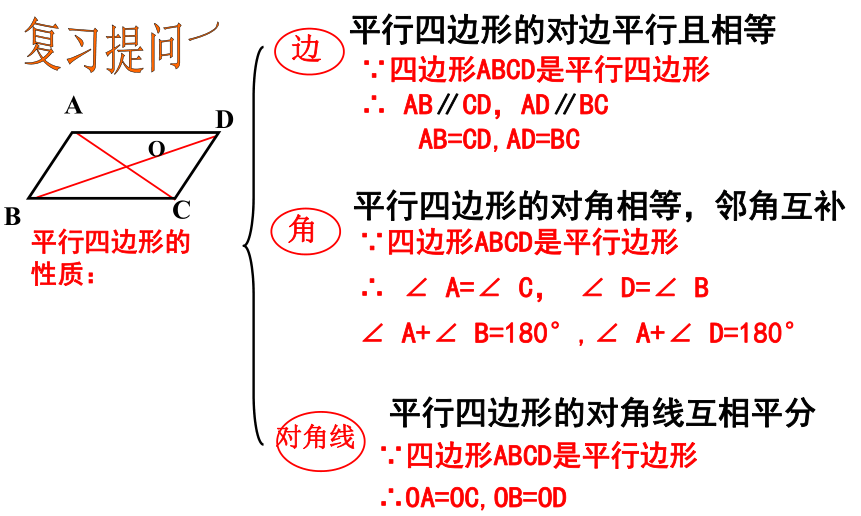 | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 16:03:21 | ||
图片预览







文档简介
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
AB=CD,AD=BC
∥
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B=180°,∠ A+∠ D=180°
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
复习提问一
复习提问二
将以上的性质定理,分别用命题形式叙述出来。
根据平行四边形的定义,我们研究了平行四边形的其它性质,那么如何来判定一个四边形是平行四边
形呢?除了定义还有什么方法?平行四边形性质定
理的逆命题是否成立?
(如果……那么……)
18.2.1平行四边形的判定(1)
1.掌握用平行四边形的定义判定一个四边形是平行四边形
2.理解并掌握两组对边分别相等、一组对边平行且相等的四边形是平行四边形;
学习目标:
重点:平行四边形的判定定理;
难点:掌握平行四边形的性质和判定的区别及熟练应用。
自学指导一:
自学课本第81-82页内容,思考并完成下列问题。
1、两组对边分别平行的四边形是平行四边形。
用几何语言如何表达定义法?
两组对边
分别平行
平行
四边形
性质
判定
定义既是性质,也是判定方法.
几何语言:
定义:两组对边分别平行的四边形是平行四边形。
∵ AD∥BC,AB∥DC
∴ 四边形ABCD是平行四边形
A
D
B
C
平行四边形的判定1(定义法)
自学指导一:
自学课本第81-82页内容,思考并完成下列问题。
5、用几何语言如何表达“两组对边分别相等的四边形是平行四边形”?
2、完成81页“思考”中的填空。
3、按82页“试一试”你有什么发现?
4、由此得到平行四边形的一种判定方法是什么?
证明你的结论并交流。
思考:
“平行四边形两组对边分别相等”中条件和结论分别是什么?它的逆命题是什么?
条件:
一个四边形是平行四边形
结论:
它的两组对边分别相等
逆命题:
两组对边分别相等的四边形是平行四边形。
这个逆命题是真命题吗?
已知:四边形ABCD,AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
∴ AB∥CD,AD∥BC
D
B
C
2
1
3
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形
证明:两组对边分别相等的四边形是平行四边形
真命题
A
B
D
C
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
几何语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
D
B
C
(2)∵ , AD = BC
∴四边形ABCD是平行四边形
基础练习:填空
(1)∵AB ∥ CD, .
∴四边形ABCD是平行四边形
AD ∥ BC
AB = CD
A
D
B
C
练习题1 已知:如图,E、F分别为平行四边形ABCD两边AD、BC的中点,连结BE、DF。求证:∠1=∠2
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,AD=BC.
又∵E、F分别是AD、BC的中点,
∴AE=CF.
∴△ABE≌△CDF(SAS)
∴BE=DF
又∵DE=BF
∴四边形BFDE是平行四边形
∴∠1=∠2
练习题2 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且AE=CF,顺次连接B、E、D,F.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF,AB=CD
∵AE=CF.
∴△ABE≌△CDF(SAS)
∴BE=DF
同理可证:DE=BF
∴四边形BFDE是平行四边形
自学指导二:
自学课本83-84页内容,思考并完成下列问题。
1.观察83页“思考” 的问题,填空。
2.按“试一试”完成“有一组对边平行且相等”的四边形,观察你所画的图形,它是平行四边形吗?
3. 试着用演绎推理证明你的发现。
4. 由此我们可以得到平行四边形的另一种判定方法是什么?怎么用几何语言来描述?
已知:如图在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
证明:一组对边平行且相等的四边形是平行四边形
D
B
C
1
2
A
证明:连接BD
∵AB∥CD
∴∠1=∠2
在△ABD和△BCD中
∴ΔABC≌ΔCDA(S.A.S.)
∴BC=DA
(两组对边分别相等的四边形是平行四边形))
∴四边形ABCD是平行四边形
AB=CD(已知)
∠1=∠2(已证)
BD=DB(公共边)
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
D
B
C
一组对边平行,另一组对边相等的四边形是平行四边形
命题:
练习
C
B
D
A
C
B
D
A
是假命题
例:已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵ AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
练习题1 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线, ∴∠ABD=∠DBE, ∵DE∥AB, ∴∠ABD=∠BDE, ∴∠DBE=∠BDE, ∴BE=DE; ∵BE=AF, ∴AF=DE; ∴四边形ADEF是平行四边形;
练习题2 已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
求证:四边形AMCN是平行四边形;
证明:
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∵M,N分别为AB和CD的中点
∴AM=AB,CN=CD
∴AM=CN,且AB∥CD
∴四边形AMCN是平行四边形
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
课堂小结
P85 练习 第2、3题
作业
结束
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
AB=CD,AD=BC
∥
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B=180°,∠ A+∠ D=180°
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
复习提问一
复习提问二
将以上的性质定理,分别用命题形式叙述出来。
根据平行四边形的定义,我们研究了平行四边形的其它性质,那么如何来判定一个四边形是平行四边
形呢?除了定义还有什么方法?平行四边形性质定
理的逆命题是否成立?
(如果……那么……)
18.2.1平行四边形的判定(1)
1.掌握用平行四边形的定义判定一个四边形是平行四边形
2.理解并掌握两组对边分别相等、一组对边平行且相等的四边形是平行四边形;
学习目标:
重点:平行四边形的判定定理;
难点:掌握平行四边形的性质和判定的区别及熟练应用。
自学指导一:
自学课本第81-82页内容,思考并完成下列问题。
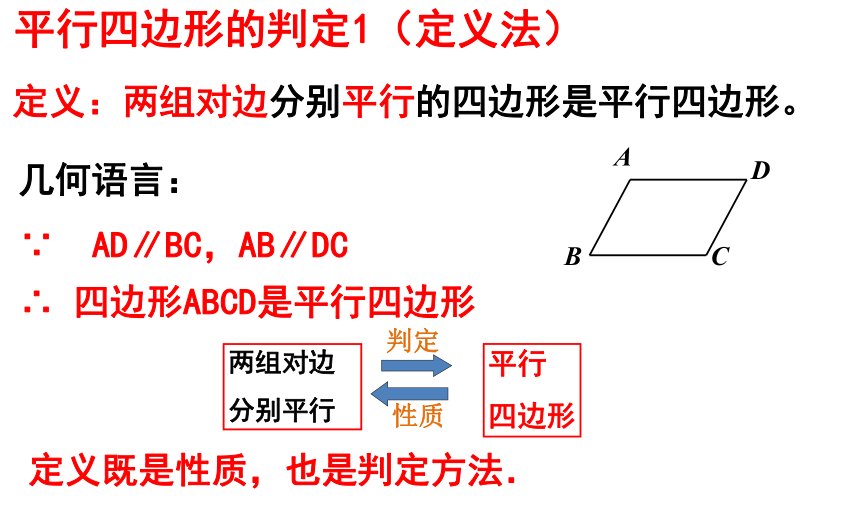
1、两组对边分别平行的四边形是平行四边形。
用几何语言如何表达定义法?
两组对边
分别平行
平行
四边形
性质
判定
定义既是性质,也是判定方法.
几何语言:
定义:两组对边分别平行的四边形是平行四边形。
∵ AD∥BC,AB∥DC
∴ 四边形ABCD是平行四边形
A
D
B
C
平行四边形的判定1(定义法)
自学指导一:
自学课本第81-82页内容,思考并完成下列问题。
5、用几何语言如何表达“两组对边分别相等的四边形是平行四边形”?
2、完成81页“思考”中的填空。
3、按82页“试一试”你有什么发现?
4、由此得到平行四边形的一种判定方法是什么?
证明你的结论并交流。
思考:
“平行四边形两组对边分别相等”中条件和结论分别是什么?它的逆命题是什么?
条件:
一个四边形是平行四边形
结论:
它的两组对边分别相等
逆命题:
两组对边分别相等的四边形是平行四边形。
这个逆命题是真命题吗?
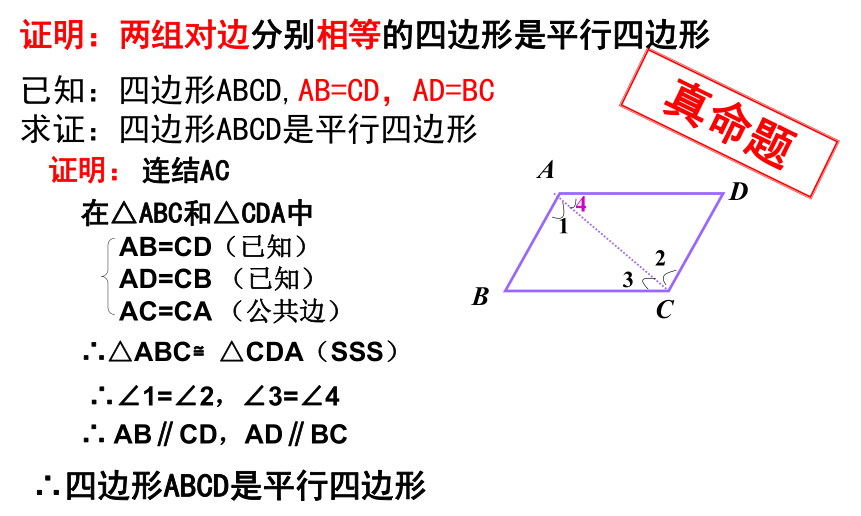
已知:四边形ABCD,AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
∴ AB∥CD,AD∥BC
D
B
C
2
1
3
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形
证明:两组对边分别相等的四边形是平行四边形
真命题
A
B
D
C
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
几何语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
D
B
C
(2)∵ , AD = BC
∴四边形ABCD是平行四边形
基础练习:填空
(1)∵AB ∥ CD, .
∴四边形ABCD是平行四边形
AD ∥ BC
AB = CD
A
D
B
C
练习题1 已知:如图,E、F分别为平行四边形ABCD两边AD、BC的中点,连结BE、DF。求证:∠1=∠2
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,AD=BC.
又∵E、F分别是AD、BC的中点,
∴AE=CF.
∴△ABE≌△CDF(SAS)
∴BE=DF
又∵DE=BF
∴四边形BFDE是平行四边形
∴∠1=∠2
练习题2 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且AE=CF,顺次连接B、E、D,F.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF,AB=CD
∵AE=CF.
∴△ABE≌△CDF(SAS)
∴BE=DF
同理可证:DE=BF
∴四边形BFDE是平行四边形
自学指导二:
自学课本83-84页内容,思考并完成下列问题。
1.观察83页“思考” 的问题,填空。
2.按“试一试”完成“有一组对边平行且相等”的四边形,观察你所画的图形,它是平行四边形吗?
3. 试着用演绎推理证明你的发现。
4. 由此我们可以得到平行四边形的另一种判定方法是什么?怎么用几何语言来描述?
已知:如图在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
证明:一组对边平行且相等的四边形是平行四边形
D
B
C
1
2
A
证明:连接BD
∵AB∥CD
∴∠1=∠2
在△ABD和△BCD中
∴ΔABC≌ΔCDA(S.A.S.)
∴BC=DA
(两组对边分别相等的四边形是平行四边形))
∴四边形ABCD是平行四边形
AB=CD(已知)
∠1=∠2(已证)
BD=DB(公共边)
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
D
B
C
一组对边平行,另一组对边相等的四边形是平行四边形
命题:
练习
C
B
D
A
C
B
D
A
是假命题
例:已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵ AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
练习题1 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线, ∴∠ABD=∠DBE, ∵DE∥AB, ∴∠ABD=∠BDE, ∴∠DBE=∠BDE, ∴BE=DE; ∵BE=AF, ∴AF=DE; ∴四边形ADEF是平行四边形;
练习题2 已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
求证:四边形AMCN是平行四边形;
证明:
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∵M,N分别为AB和CD的中点
∴AM=AB,CN=CD
∴AM=CN,且AB∥CD
∴四边形AMCN是平行四边形
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
课堂小结
P85 练习 第2、3题
作业
结束
