华东师大版八年级下册19.2 .1菱形性质课件 ( 共17张PPT)
文档属性
| 名称 | 华东师大版八年级下册19.2 .1菱形性质课件 ( 共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览




文档简介
19.2 .1 菱形的性质
知识回顾
平行四边形的对边平行且相等;
平行线之间的距离处处相等
平行四边形的概念及性质
平行四边形的对角相等、邻角互补;
平行四边形的对角线互相平分 ;
平行四边形是中心对称图形 .
矩形的概念及性质
矩形:有一个角是直角的特殊平行四边形.
矩形的性质:
矩形的对角线相等且互相平分.
矩形具有平行四边形的所有性质 ;
矩形的四个内角都是直角;
矩形既是轴对称图形又是中心对称图形 ;
知识回顾
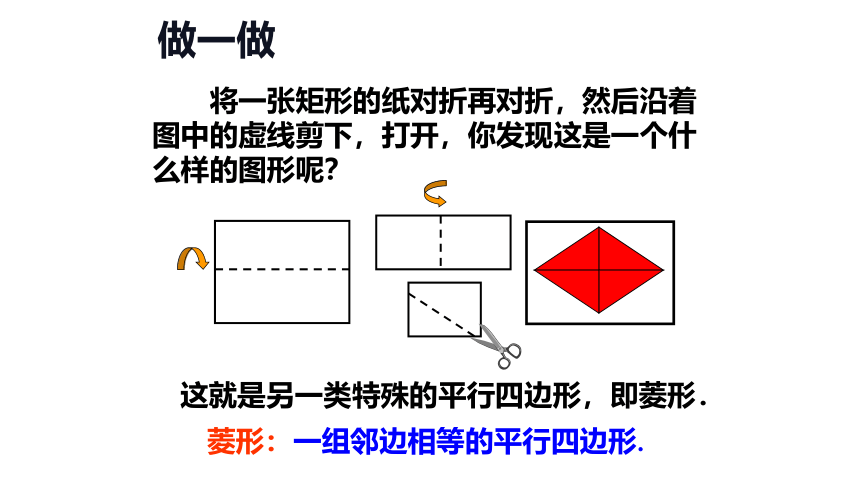
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
做一做
菱形:一组邻边相等的平行四边形.
这就是另一类特殊的平行四边形,即菱形.
有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形,它具有平行四边形的一切性质.
对边相等.
对角相等.
对角线互相平分.
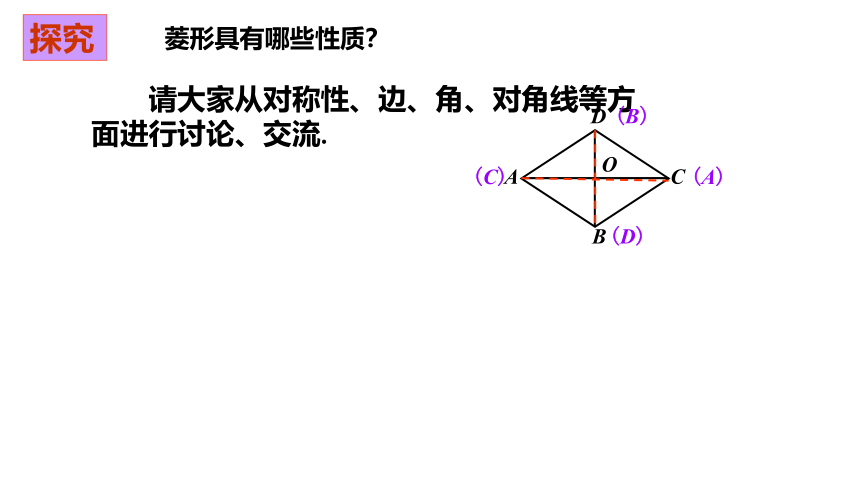
探究
菱形具有哪些性质?
请大家从对称性、边、角、对角线等方面进行讨论、交流.
A
O
D
C
B
(A)
(B)
(C)
(D)
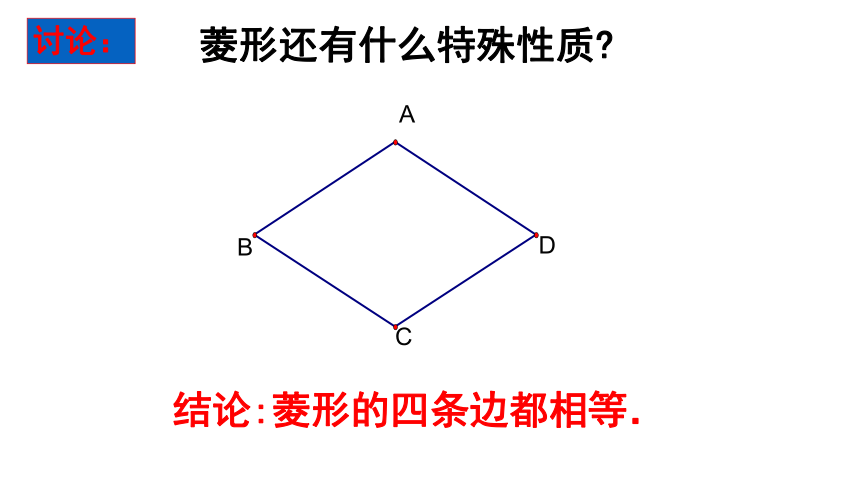
讨论:
D
A
C
B
菱形还有什么特殊性质?
结论:菱形的四条边都相等.
讨论:
D
O
A
C
B
⒉连结菱形ABCD的对角线AC、BD相交于点O.
你还有什么发现?
结论:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
探究
1、 菱形是中心图形吗?如果是,对称中心在哪里?
2、 菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴在哪里?对称轴之间有什么位置关系?
探究:如图,菱形ABCD被对角线AC、BD分成__ 个_____的直角三角形,设菱形的两条对角线长分别为a和b,则每个直角三角形的两直角边长分别为
_______.
你能利用三角形的面积公式探究出菱形ABCD的面积S与a、b的关系吗?
S菱形ABCD =
或
S菱形ABCD=底×高
a
b
全等
四
1.菱形是特殊的平行四边形,具备平行四边形的所有性质.
2.菱形是中心对称图形,对称中心为它的对角线的交点;也是轴对称图形,对称轴为它的对角线所在的直线(有两条对称轴).
3.菱形的四条边都相等.
4.菱形的两条对角线互相垂直平分,并且分别平分每一组对角.
归纳总结:菱形的性质
例题讲解
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形.
(1)在菱形ABCD中,
∠B+∠BAD=180?(两直线平行同旁内角互补).
又因为∠BAD=2∠B,
所以∠B=60?.
(2)在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等).
所以在△ABC中,∠BAC=∠BCA(等边对等角).
又因为∠B+∠BAC+∠BCA=180?(三角形内角和定理),
所以∠BAC=∠BCA=∠B=60?.
所以AB=BC=AC(等角对等边).
即ABC是等边三角形.
AD∥BC,
D
O
A
C
B
例⒈在菱形ABCD中,对角线AC、BD的长分别为a、b,AC、BD相交于点O.
⑴用含a、b的代数式表示菱形ABCD的面积S.
⑵若a=3cm,b=4cm,求菱形ABCD的面积和周长.
例题讲解
例题精析
例2.如图,菱形ABCD中,E是AB的中点,且DE⊥AB.(1)求∠ABD的度数;(2)若菱形的边长为2,求菱形的面积.
A
B
C
D
E
打好基础:
比一比,看谁的反应最快!
1、下列说法中错误的是( )
A、一组邻边相等的平行四边形是菱形;
B、对角线互相垂直的平行四边形是菱形;
C、对角线互相平分的四边形是菱形;
D、菱形的每一条对角线平分一组对角.
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段, 既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为_____.
52
C
D
巩固练习
2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______.
1.菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为______;边长为______.
3.已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是
__________.
8cm
5cm
64cm
12cm,16cm
课堂小结
矩形
菱形
定义
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
性
质
1.具有平行四边形的一切性质;
2.四个角都是直角;
3.矩形的对角线相等.
1.具有平行四边形的一切性质;
2.菱形的四条边都相等;
3.菱形的对角线互相垂直,并且每一条对角线平分一组对角.
矩形和菱形的性质
菱形的面积等于两条对角线长的乘积的一半.
菱形既是轴对称图形,又是中心对称图形.
对称轴是对角线所在的直线,对称中心是两条对角线的交点.
知识回顾
平行四边形的对边平行且相等;
平行线之间的距离处处相等
平行四边形的概念及性质
平行四边形的对角相等、邻角互补;
平行四边形的对角线互相平分 ;
平行四边形是中心对称图形 .
矩形的概念及性质
矩形:有一个角是直角的特殊平行四边形.
矩形的性质:
矩形的对角线相等且互相平分.
矩形具有平行四边形的所有性质 ;
矩形的四个内角都是直角;
矩形既是轴对称图形又是中心对称图形 ;
知识回顾
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
做一做
菱形:一组邻边相等的平行四边形.
这就是另一类特殊的平行四边形,即菱形.
有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形,它具有平行四边形的一切性质.
对边相等.
对角相等.
对角线互相平分.
探究
菱形具有哪些性质?
请大家从对称性、边、角、对角线等方面进行讨论、交流.
A
O
D
C
B
(A)
(B)
(C)
(D)
讨论:
D
A
C
B
菱形还有什么特殊性质?
结论:菱形的四条边都相等.
讨论:
D
O
A
C
B
⒉连结菱形ABCD的对角线AC、BD相交于点O.
你还有什么发现?
结论:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
探究
1、 菱形是中心图形吗?如果是,对称中心在哪里?
2、 菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴在哪里?对称轴之间有什么位置关系?
探究:如图,菱形ABCD被对角线AC、BD分成__ 个_____的直角三角形,设菱形的两条对角线长分别为a和b,则每个直角三角形的两直角边长分别为
_______.
你能利用三角形的面积公式探究出菱形ABCD的面积S与a、b的关系吗?
S菱形ABCD =
或
S菱形ABCD=底×高
a
b
全等
四
1.菱形是特殊的平行四边形,具备平行四边形的所有性质.
2.菱形是中心对称图形,对称中心为它的对角线的交点;也是轴对称图形,对称轴为它的对角线所在的直线(有两条对称轴).
3.菱形的四条边都相等.
4.菱形的两条对角线互相垂直平分,并且分别平分每一组对角.
归纳总结:菱形的性质
例题讲解
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形.
(1)在菱形ABCD中,
∠B+∠BAD=180?(两直线平行同旁内角互补).
又因为∠BAD=2∠B,
所以∠B=60?.
(2)在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等).
所以在△ABC中,∠BAC=∠BCA(等边对等角).
又因为∠B+∠BAC+∠BCA=180?(三角形内角和定理),
所以∠BAC=∠BCA=∠B=60?.
所以AB=BC=AC(等角对等边).
即ABC是等边三角形.
AD∥BC,
D
O
A
C
B
例⒈在菱形ABCD中,对角线AC、BD的长分别为a、b,AC、BD相交于点O.
⑴用含a、b的代数式表示菱形ABCD的面积S.
⑵若a=3cm,b=4cm,求菱形ABCD的面积和周长.
例题讲解
例题精析
例2.如图,菱形ABCD中,E是AB的中点,且DE⊥AB.(1)求∠ABD的度数;(2)若菱形的边长为2,求菱形的面积.
A
B
C
D
E
打好基础:
比一比,看谁的反应最快!
1、下列说法中错误的是( )
A、一组邻边相等的平行四边形是菱形;
B、对角线互相垂直的平行四边形是菱形;
C、对角线互相平分的四边形是菱形;
D、菱形的每一条对角线平分一组对角.
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段, 既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为_____.
52
C
D
巩固练习
2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______.
1.菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为______;边长为______.
3.已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是
__________.
8cm
5cm
64cm
12cm,16cm
课堂小结
矩形
菱形
定义
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
性
质
1.具有平行四边形的一切性质;
2.四个角都是直角;
3.矩形的对角线相等.
1.具有平行四边形的一切性质;
2.菱形的四条边都相等;
3.菱形的对角线互相垂直,并且每一条对角线平分一组对角.
矩形和菱形的性质
菱形的面积等于两条对角线长的乘积的一半.
菱形既是轴对称图形,又是中心对称图形.
对称轴是对角线所在的直线,对称中心是两条对角线的交点.
