华东师大版七年级数学下册第7章7.4实践与探索教学课件(17张ppt)
文档属性
| 名称 | 华东师大版七年级数学下册第7章7.4实践与探索教学课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览





文档简介
7.4 实践与探索
导入新课
讲授新课
当堂练习
课堂小结
鸡兔同笼
源于我国古代《孙子算经》
“雉(鸡)兔同笼”题:今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?
看课本 15页阅读材料最后一段第一行。
看课本 44页阅读材料,体会我国古代在数学上的伟大成就。
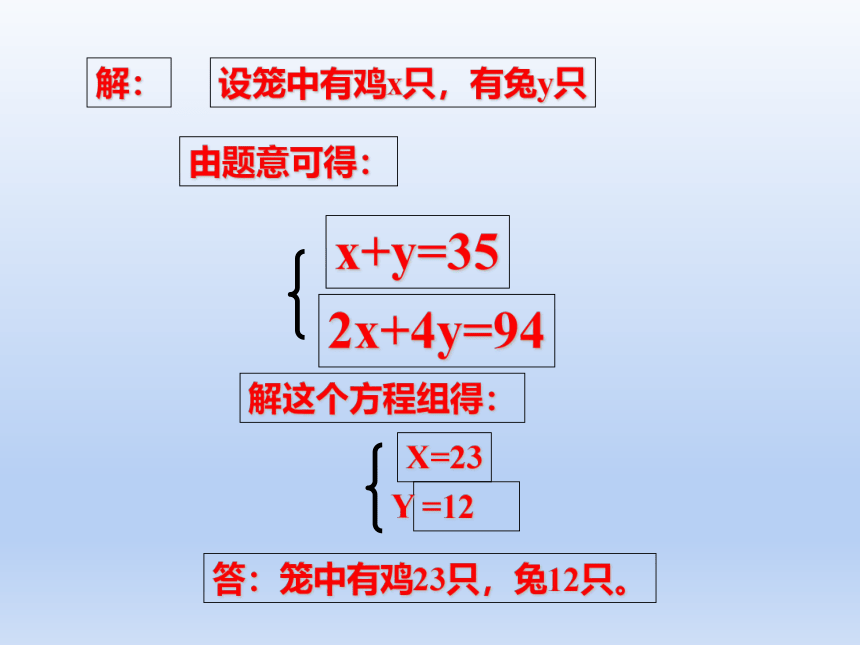
解:
设笼中有鸡x只,有兔y只
由题意可得:
x+y=35
2x+4y=94
解这个方程组得:
X=23
=12
答:笼中有鸡23只,兔12只。
Y
学习目标
学会用二元一次方程组(或三元一次方程组)
来解决实际问题.(难点)
导入新课
问题引入
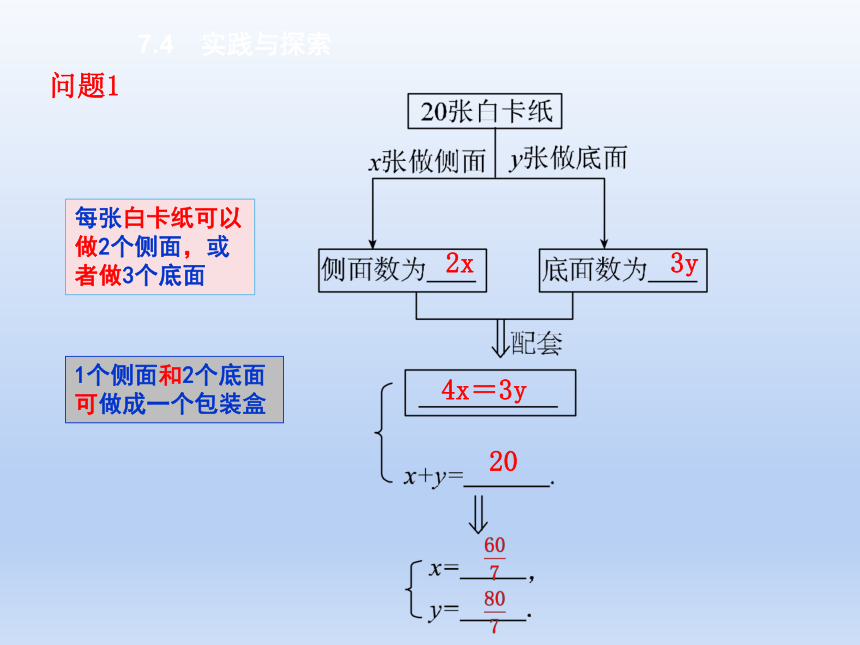
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面。已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
7.4 实践与探索
问题1
2x
3y
4x=3y
20
每张白卡纸可以做2个侧面,或者做3个底面
1个侧面和2个底面可做成一个包装盒
解:设用x张白卡纸做盒身,用y张白卡纸做盒底盖,由题意得
所以可做16个包装盒.
解得
问题:要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面。已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
由于解是分数,所以若白卡纸不套裁, 8张白卡纸做侧面,可做16个侧面,则最多能做成16个包装盒;
想一想:如果一张白卡纸可以适当的套裁出一个侧面和一个底面,那么,又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分地利用白卡纸?
若可套裁
用8张做侧面,可做8×2=16(个)侧面;
11张做底面,可做11×3=33(个)底面;
将余下的一张白卡纸剪成两半:
一半做1个侧面,另一半做1个底面,则共可做侧面17个,底面34个,正好配成17个包装盒,较充分地利用了材料.
问题2: 小明在拼图时,发现8个一样大小的长方形如图那样,恰好拼成一个大长方形.
小红看见了,说:“我来试一试。”结果七拼八凑,拼成如图那样的正方形。咳,怎么中间还留下了一个洞,恰好是边长为2的 小正方形!
2
你能求出这些长方形的长和宽吗?
- 8× =22
即(x+2y)2-8xy=4
所得到的方程不是我们所学过的方程,没办法求解,怎么办?
3x=5y
2y=x+2
解:设每个小长方形的长为xmm,宽为ymm,根据题意,得:
解这个方程组,得
x=10
y=6
{
{
探索问题(2),由图7.4.1能得出小长方形的长(x)和宽(y)的关系是
____________;
(2)由图7.4.2能得出小长方形的长和宽的关系是
____________.
你能把这个问题的解答过程写出来吗?
3x=5y
x+2=2y
经检验,符合题意。
答:这些长方形的长为10mm,宽为6mm。
.如图,用8块相同的小长方形地砖拼成一个大的长方形图案,已知大长方形的周长为200cm,那么每个小长方形地砖的面积是多少?
解:设小长方形的长为x cm,宽为y cm,
根据题意,则:
解得
x=30,
y=10.
答:每个小长方形的面积为300cm2.
所以每个小长方形的面积等于30×10=300cm2.
x x
y x y y
y
x
练一练
探索最优方案:
某物流公司现有31吨货物需运往某地,计划同时租用A型车a辆,B型车b辆,使每辆车都装满货物且恰好一次运完。已知每种型号车的载重量和租金如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}车型
A
B
载重量(吨/辆)
3
4
租金(元/辆)
1000
1200
(1)请你帮该物流公司设计租车方案;
(2)请选出最省钱的租车方案,并求出最少租车费用。
∵a,b均为正整数,
a=9 或 a=5 或 a=1
∴ b=1 b=4 b=7
解:(1)根据题意得:3a+4b=31
∴有3种租车方案:?租用A型车9辆,B型车1辆;?租用A型车5辆,B型车4辆;?租用A型车1辆,B型车7辆.
(2)方案?需租金9×1000+1200=10200(元)
方案?需租金5×1000+4×1200=9800(元)
方案?需租金1×1000+7×1200=9400(元)
∵10200>9800>9400
∴最省钱的租车方案是租用A型车1辆,B型车7辆,最少租车费用为9400元。
课本43页习题7.4第1、2题
1.某市为更有效地利用水资源,制定了用水标准:
如果一户三口之家每月用水量不超过Am3 ,按每立方米水1.30元收费;如果超过Am3 ,超过部分按每立方米水2.90元收费,其余仍按按每立方米水1.30元收费.小红一家三人,1月份共用水12 m3 ,支付水费22元.问该市制定的用水标准A为多少?小红一家超过部分的用水是多少立方米?
解:设用水标准A为x m3,小红一家超标使用了ym3 的水,根据题意得:
x + y = 12,
1.30x + 2.90y = 22.
解得
答:用水标准A为8 m3,小红一家超标使用了4m3 的水.
课本43页习题7.4第1、2题
2.长风乐园的门票价格规定如下表所列.某校七年级(1)、(2)两个班共104人去游长风乐园,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算,如果两班都以班为单位分别购票,则一共应付1240元;如果两班联合起来,作为一个团体购票,则可以节省不少钱.问两班各有多少名学生?
购票人数(人)
1~50
51~100
100以上
每人门票价(元)
13
11
9
解:设七年级(1)班有x 人,(2)班有y人,根据题意得:
x + y = 104,
13x +11 y = 1240.
解得
答:七年级(1)班有48人,(2)班有56人.
课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
? 2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
课后作业
课本46页复习题C组题
导入新课
讲授新课
当堂练习
课堂小结
鸡兔同笼
源于我国古代《孙子算经》
“雉(鸡)兔同笼”题:今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?
看课本 15页阅读材料最后一段第一行。
看课本 44页阅读材料,体会我国古代在数学上的伟大成就。
解:
设笼中有鸡x只,有兔y只
由题意可得:
x+y=35
2x+4y=94
解这个方程组得:
X=23
=12
答:笼中有鸡23只,兔12只。
Y
学习目标
学会用二元一次方程组(或三元一次方程组)
来解决实际问题.(难点)
导入新课
问题引入
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面。已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
7.4 实践与探索
问题1
2x
3y
4x=3y
20
每张白卡纸可以做2个侧面,或者做3个底面
1个侧面和2个底面可做成一个包装盒
解:设用x张白卡纸做盒身,用y张白卡纸做盒底盖,由题意得
所以可做16个包装盒.
解得
问题:要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面。已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
由于解是分数,所以若白卡纸不套裁, 8张白卡纸做侧面,可做16个侧面,则最多能做成16个包装盒;
想一想:如果一张白卡纸可以适当的套裁出一个侧面和一个底面,那么,又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分地利用白卡纸?
若可套裁
用8张做侧面,可做8×2=16(个)侧面;
11张做底面,可做11×3=33(个)底面;
将余下的一张白卡纸剪成两半:
一半做1个侧面,另一半做1个底面,则共可做侧面17个,底面34个,正好配成17个包装盒,较充分地利用了材料.
问题2: 小明在拼图时,发现8个一样大小的长方形如图那样,恰好拼成一个大长方形.
小红看见了,说:“我来试一试。”结果七拼八凑,拼成如图那样的正方形。咳,怎么中间还留下了一个洞,恰好是边长为2的 小正方形!
2
你能求出这些长方形的长和宽吗?
- 8× =22
即(x+2y)2-8xy=4
所得到的方程不是我们所学过的方程,没办法求解,怎么办?
3x=5y
2y=x+2
解:设每个小长方形的长为xmm,宽为ymm,根据题意,得:
解这个方程组,得
x=10
y=6
{
{
探索问题(2),由图7.4.1能得出小长方形的长(x)和宽(y)的关系是
____________;
(2)由图7.4.2能得出小长方形的长和宽的关系是
____________.
你能把这个问题的解答过程写出来吗?
3x=5y
x+2=2y
经检验,符合题意。
答:这些长方形的长为10mm,宽为6mm。
.如图,用8块相同的小长方形地砖拼成一个大的长方形图案,已知大长方形的周长为200cm,那么每个小长方形地砖的面积是多少?
解:设小长方形的长为x cm,宽为y cm,
根据题意,则:
解得
x=30,
y=10.
答:每个小长方形的面积为300cm2.
所以每个小长方形的面积等于30×10=300cm2.
x x
y x y y
y
x
练一练
探索最优方案:
某物流公司现有31吨货物需运往某地,计划同时租用A型车a辆,B型车b辆,使每辆车都装满货物且恰好一次运完。已知每种型号车的载重量和租金如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}车型
A
B
载重量(吨/辆)
3
4
租金(元/辆)
1000
1200
(1)请你帮该物流公司设计租车方案;
(2)请选出最省钱的租车方案,并求出最少租车费用。
∵a,b均为正整数,
a=9 或 a=5 或 a=1
∴ b=1 b=4 b=7
解:(1)根据题意得:3a+4b=31
∴有3种租车方案:?租用A型车9辆,B型车1辆;?租用A型车5辆,B型车4辆;?租用A型车1辆,B型车7辆.
(2)方案?需租金9×1000+1200=10200(元)
方案?需租金5×1000+4×1200=9800(元)
方案?需租金1×1000+7×1200=9400(元)
∵10200>9800>9400
∴最省钱的租车方案是租用A型车1辆,B型车7辆,最少租车费用为9400元。
课本43页习题7.4第1、2题
1.某市为更有效地利用水资源,制定了用水标准:
如果一户三口之家每月用水量不超过Am3 ,按每立方米水1.30元收费;如果超过Am3 ,超过部分按每立方米水2.90元收费,其余仍按按每立方米水1.30元收费.小红一家三人,1月份共用水12 m3 ,支付水费22元.问该市制定的用水标准A为多少?小红一家超过部分的用水是多少立方米?
解:设用水标准A为x m3,小红一家超标使用了ym3 的水,根据题意得:
x + y = 12,
1.30x + 2.90y = 22.
解得
答:用水标准A为8 m3,小红一家超标使用了4m3 的水.
课本43页习题7.4第1、2题
2.长风乐园的门票价格规定如下表所列.某校七年级(1)、(2)两个班共104人去游长风乐园,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算,如果两班都以班为单位分别购票,则一共应付1240元;如果两班联合起来,作为一个团体购票,则可以节省不少钱.问两班各有多少名学生?
购票人数(人)
1~50
51~100
100以上
每人门票价(元)
13
11
9
解:设七年级(1)班有x 人,(2)班有y人,根据题意得:
x + y = 104,
13x +11 y = 1240.
解得
答:七年级(1)班有48人,(2)班有56人.
课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
? 2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
课后作业
课本46页复习题C组题
