华东师大版七年级数学下册课件:9.1.2-三角形的内角和与外角和(共18张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册课件:9.1.2-三角形的内角和与外角和(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:14:06 | ||
图片预览


文档简介
9.1.2 三角形的内角和与外角和
A
B
C
复习
你还记得三角形的内角和是多少吗?
你还能证明它吗?
A
B
C
D
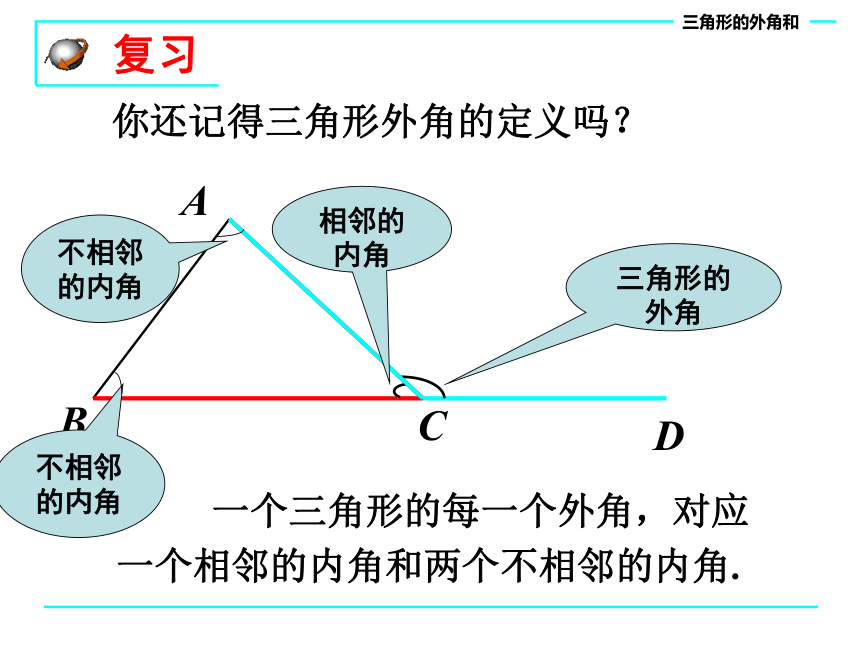
一个三角形的每一个外角,对应一个相邻的内角和两个不相邻的内角.
相邻的
内角
三角形的外角
复习
你还记得三角形外角的定义吗?
不相邻的内角
不相邻的内角
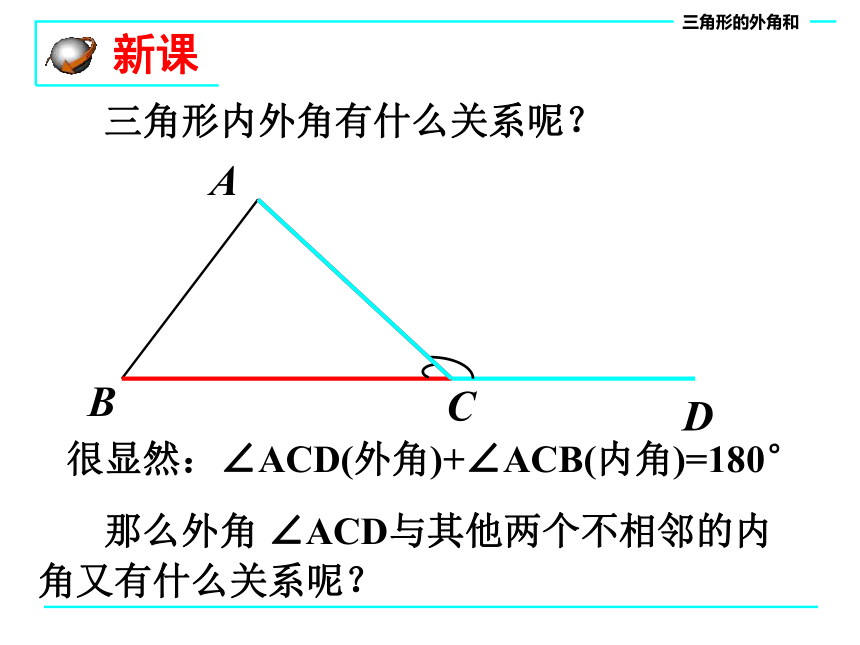
新课
三角形内外角有什么关系呢?
B
C
D
A
很显然:∠ACD(外角)+∠ACB(内角)=180°
那么外角 ∠ACD与其他两个不相邻的内角又有什么关系呢?
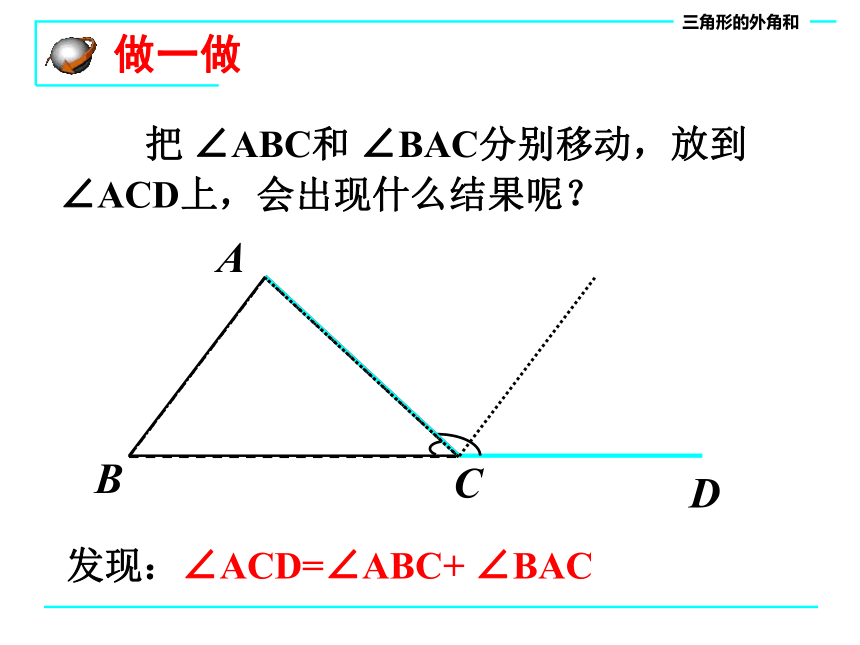
做一做
B
C
A
D
把 ∠ABC和 ∠BAC分别移动,放到 ∠ACD上,会出现什么结果呢?
发现:∠ACD=∠ABC+ ∠BAC
三角形外角的性质
∠ACD=∠ABC+ ∠BAC
即:三角形的一个外角等于与它不相邻的两个内角的和.
可知:三角形的一个外角大于任何一个与它不相邻的内角.
因为:∠ACD+∠ACB=180°
∠ABC+ ∠BAC+ ∠ACB=180 °
B
C
A
)
)
)
1
2
3
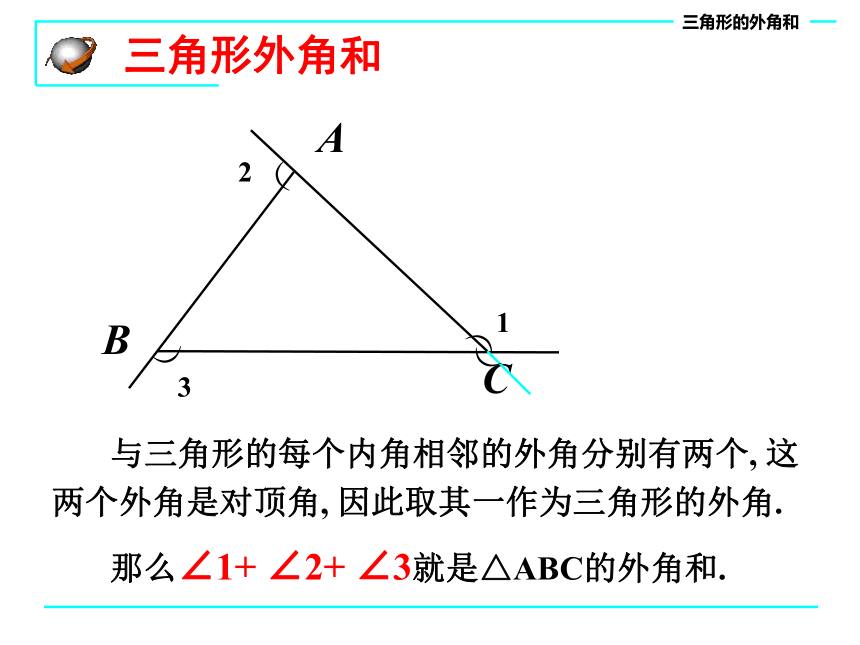
三角形外角和
)
与三角形的每个内角相邻的外角分别有两个, 这两个外角是对顶角, 因此取其一作为三角形的外角.
那么∠1+ ∠2+ ∠3就是△ABC的外角和.
三角形外角和
B
C
A
)
)
)
1
2
3
所以:∠1+ ∠2+ ∠3= 360 °
∠1+ = 180 °
∠2+ = 180 °
∠3+ = 180 °
三式相加可以得到
∠1+ ∠2+ ∠3+ + + = .
∠ACB
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
540 °
而 ∠ACB +∠BAC +∠ABC= 180 °
三角形外角和等于360 °
例题解析
例:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
80°
70°
?
?
∵∠ADC是△ABD的外角(已知)
解:
∴∠ADC=∠B+∠BAD=80°
又∵∠B=∠BAD(已知)
(三角形的一个外角等于与它不
相邻的两个内角的和 )
∴∠B=80°×
=40°(等量代换)
练习
1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系______________________.
A
B
C
D
P
1
2
∠A< ∠2< ∠1
求证: ∠A<∠1
20°
30°
51°
若∠ABP=20°∠ACP=30°
∠A=51°,
求∠1的度数?
2、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
∴ ∠A+∠B+∠C+∠D+∠E
=∠1+∠2+∠C
=180°
练习
3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______
A
D
E
C
B
1
4
3
2
30°
练习
1、三角形内角和为180°;
2、三角形外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
反思
课本59页练习
作业
1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______
1
课外作业
2、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
课外作业
3. 如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
课外作业
如果你想学会游泳,你必须下水;
如果想成为解题能手,你必须解题.
——(数学家)波利亚
If?you?wish?to?learn?swimming,you?have?to?go into?the?water, and if you?wish?to?become?a?problem?solver,you have?to?solve?problems.
数学名言
A
B
C
复习
你还记得三角形的内角和是多少吗?
你还能证明它吗?
A
B
C
D
一个三角形的每一个外角,对应一个相邻的内角和两个不相邻的内角.
相邻的
内角
三角形的外角
复习
你还记得三角形外角的定义吗?
不相邻的内角
不相邻的内角
新课
三角形内外角有什么关系呢?
B
C
D
A
很显然:∠ACD(外角)+∠ACB(内角)=180°
那么外角 ∠ACD与其他两个不相邻的内角又有什么关系呢?
做一做
B
C
A
D
把 ∠ABC和 ∠BAC分别移动,放到 ∠ACD上,会出现什么结果呢?
发现:∠ACD=∠ABC+ ∠BAC
三角形外角的性质
∠ACD=∠ABC+ ∠BAC
即:三角形的一个外角等于与它不相邻的两个内角的和.
可知:三角形的一个外角大于任何一个与它不相邻的内角.
因为:∠ACD+∠ACB=180°
∠ABC+ ∠BAC+ ∠ACB=180 °
B
C
A
)
)
)
1
2
3
三角形外角和
)
与三角形的每个内角相邻的外角分别有两个, 这两个外角是对顶角, 因此取其一作为三角形的外角.
那么∠1+ ∠2+ ∠3就是△ABC的外角和.
三角形外角和
B
C
A
)
)
)
1
2
3
所以:∠1+ ∠2+ ∠3= 360 °
∠1+ = 180 °
∠2+ = 180 °
∠3+ = 180 °
三式相加可以得到
∠1+ ∠2+ ∠3+ + + = .
∠ACB
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
540 °
而 ∠ACB +∠BAC +∠ABC= 180 °
三角形外角和等于360 °
例题解析
例:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
80°
70°
?
?
∵∠ADC是△ABD的外角(已知)
解:
∴∠ADC=∠B+∠BAD=80°
又∵∠B=∠BAD(已知)
(三角形的一个外角等于与它不
相邻的两个内角的和 )
∴∠B=80°×
=40°(等量代换)
练习
1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系______________________.
A
B
C
D
P
1
2
∠A< ∠2< ∠1
求证: ∠A<∠1
20°
30°
51°
若∠ABP=20°∠ACP=30°
∠A=51°,
求∠1的度数?
2、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
∴ ∠A+∠B+∠C+∠D+∠E
=∠1+∠2+∠C
=180°
练习
3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______
A
D
E
C
B
1
4
3
2
30°
练习
1、三角形内角和为180°;
2、三角形外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
反思
课本59页练习
作业
1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______
1
课外作业
2、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
课外作业
3. 如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
课外作业
如果你想学会游泳,你必须下水;
如果想成为解题能手,你必须解题.
——(数学家)波利亚
If?you?wish?to?learn?swimming,you?have?to?go into?the?water, and if you?wish?to?become?a?problem?solver,you have?to?solve?problems.
数学名言
