华东师大版七年级数学下册课件:9.3.2用多种正多边形(共26张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册课件:9.3.2用多种正多边形(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 714.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:40:46 | ||
图片预览



文档简介
9.3 用正多边形铺设地面
2.用多种正多边形
复习回顾
用一种正多边形铺设的规律:正多边形的一个内角是360°的约数(或360°是这个正多边形一个内角的整数倍)!
围绕一个顶点拼在一起的几个内角加在一起恰好组成一个周角( 360°).
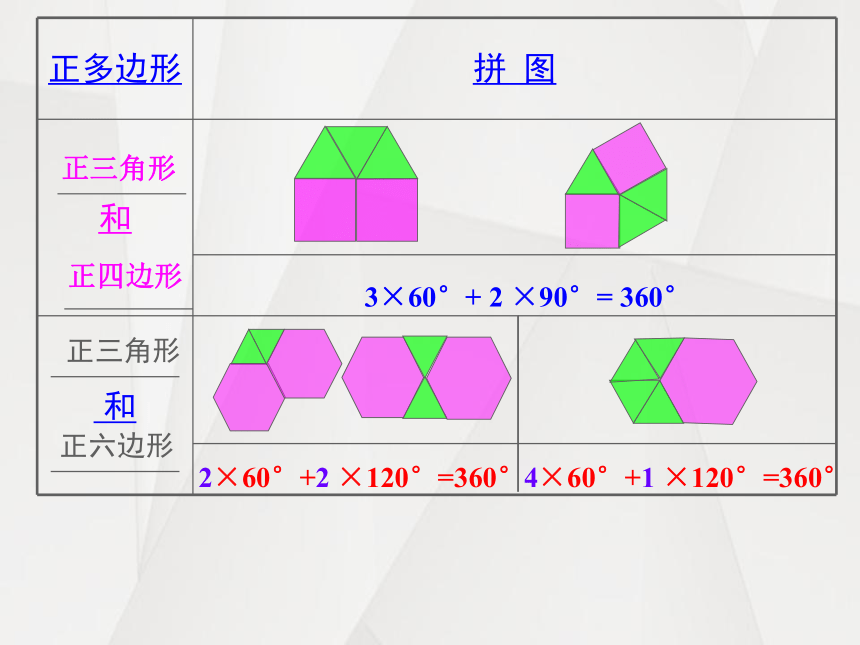
正多边形
拼 图
和
和
3×60°+ 2 ×90°= 360°
2×60°+2 ×120°=360°
4×60°+1 ×120°=360°
正三角形
正四边形
正三角形
正六边形
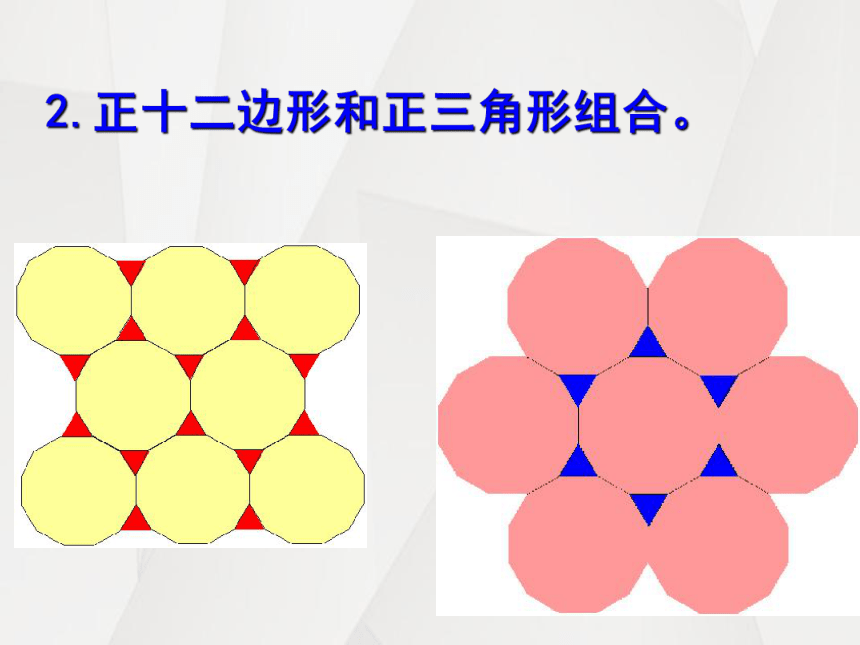
2.正十二边形和正三角形组合。
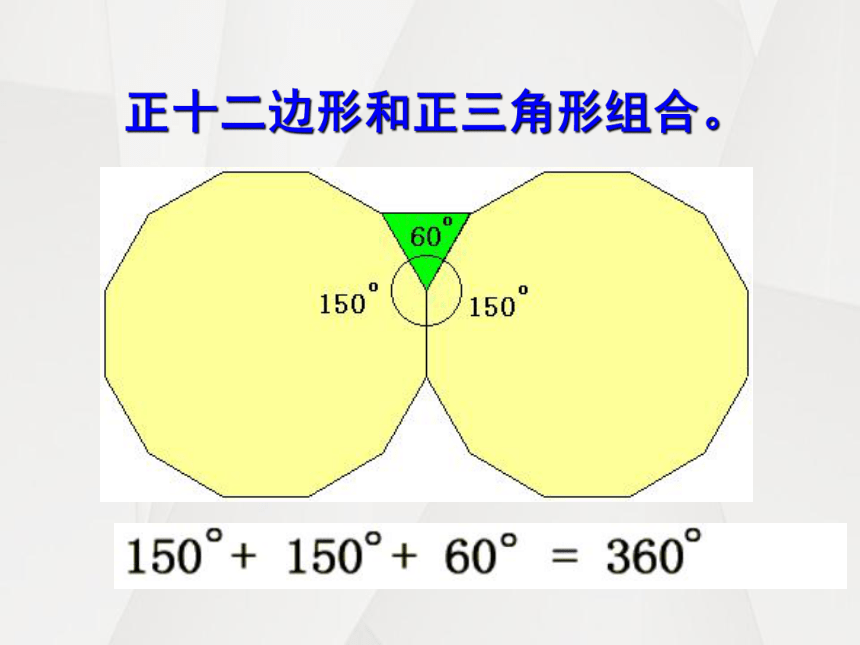
正十二边形和正三角形组合。
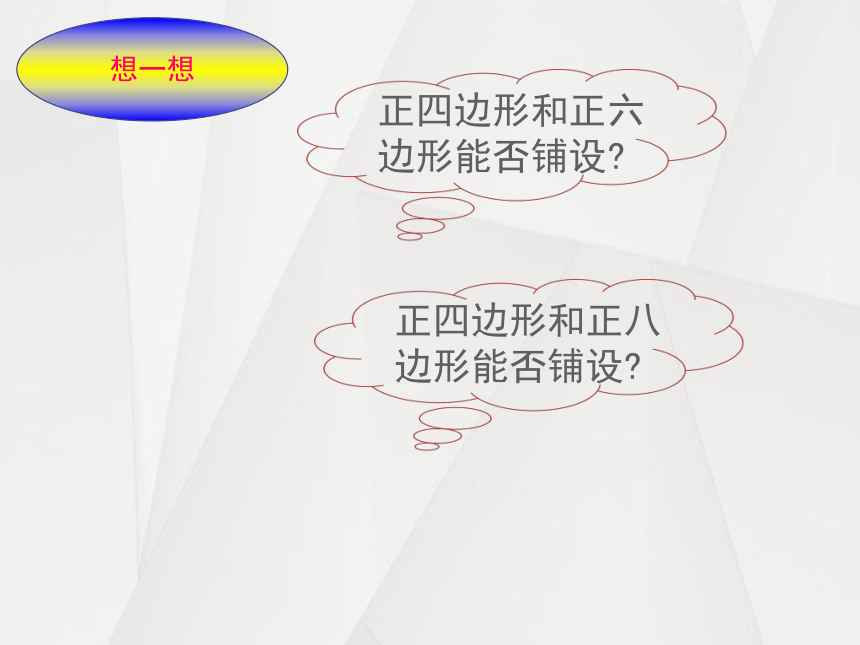
想一想
正四边形和正六边形能否铺设?
正四边形和正八边形能否铺设?
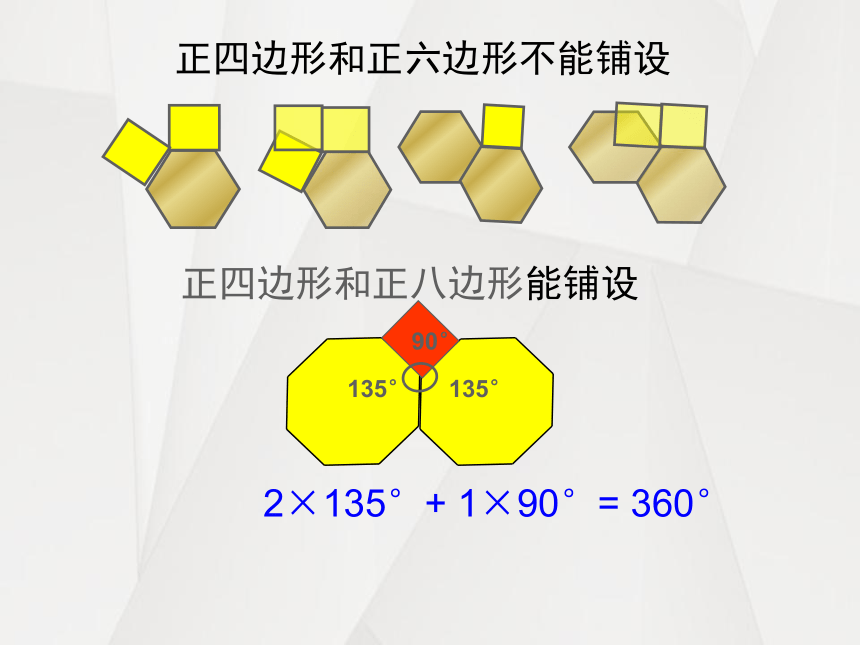
正四边形和正六边形不能铺设
正四边形和正八边形能铺设
90°
135°
135°
2×135°+ 1×90°= 360°
你能总结其中的规律吗?
得出结论:
用两种正多边形铺设的规律:
拼接在同一个点的各个角的和恰好等于360°(周角)
用两种正多边形铺设的情况有:
1、正三角形和正四边形
(3×60°+ 2 ×90°= 360°)
2、正三角形和正六边形
(2× 60°+ +2 ×120°= 360° )
( 4×60°+1 ×120°=360°)
3、正三边形和正十二边形
(1× 60°+ 2 ×150°= 360°)
4、正四边形和正八边形
(2×135°+ 1×90°= 360°)
探究:
用几个形状、大小相同的任意三角形能铺设成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
同一种任意三角形能铺设成平面图案。
1
4
3
2
1
4
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以同一种任意四边形能铺设成平面图案。
1.不能铺设成平面图案的正多边形组合为( )
A.正八边形和正方形 B.正三角形和正四边形
C.正六边形和正三角形 D.正六边形和正八边形
D
练习
2.用正三角形和正十二边形铺设,可能情况有( )
A.1种 B.2种 C.3种 C.4种
A
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形的角,则有
2m+5n=12
m=1
n=2
m·60 +n·150=360
。
。
。
∵ m,n 为正整数
∴解为
3.用正三角形和正六边形铺设地面,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式是( )
A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6
D
m+2·n=6
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,则有
那么用三种正多边形:正三角形、正方形、正六边形能否进行平面铺设?如果不能铺设,为什么?如果能,你能把它画出来吗(草图)?
拓展延伸
正六边形、正方形、正三角形
正十二边形、正六边形和正方形的组合。
正十二边形、正方形、正三角形
用三种正多边形铺设的情况:
1、正三边形、正四边形和正六边形
2、正四边形、正六边形和正十二边形
3、正三边形、正四边形和正十二边形
(1×60°+ 2 ×90°+ 120° = 360°)
(1×90°+ 1×120°+1 ×150° = 360°)
(2×60°+ 1 ×90°+ 1× 120° = 360°)
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
2.用多种正多边形
复习回顾
用一种正多边形铺设的规律:正多边形的一个内角是360°的约数(或360°是这个正多边形一个内角的整数倍)!
围绕一个顶点拼在一起的几个内角加在一起恰好组成一个周角( 360°).
正多边形
拼 图
和
和
3×60°+ 2 ×90°= 360°
2×60°+2 ×120°=360°
4×60°+1 ×120°=360°
正三角形
正四边形
正三角形
正六边形
2.正十二边形和正三角形组合。
正十二边形和正三角形组合。
想一想
正四边形和正六边形能否铺设?
正四边形和正八边形能否铺设?
正四边形和正六边形不能铺设
正四边形和正八边形能铺设
90°
135°
135°
2×135°+ 1×90°= 360°
你能总结其中的规律吗?
得出结论:
用两种正多边形铺设的规律:
拼接在同一个点的各个角的和恰好等于360°(周角)
用两种正多边形铺设的情况有:
1、正三角形和正四边形
(3×60°+ 2 ×90°= 360°)
2、正三角形和正六边形
(2× 60°+ +2 ×120°= 360° )
( 4×60°+1 ×120°=360°)
3、正三边形和正十二边形
(1× 60°+ 2 ×150°= 360°)
4、正四边形和正八边形
(2×135°+ 1×90°= 360°)
探究:
用几个形状、大小相同的任意三角形能铺设成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
同一种任意三角形能铺设成平面图案。
1
4
3
2
1
4
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以同一种任意四边形能铺设成平面图案。
1.不能铺设成平面图案的正多边形组合为( )
A.正八边形和正方形 B.正三角形和正四边形
C.正六边形和正三角形 D.正六边形和正八边形
D
练习
2.用正三角形和正十二边形铺设,可能情况有( )
A.1种 B.2种 C.3种 C.4种
A
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形的角,则有
2m+5n=12
m=1
n=2
m·60 +n·150=360
。
。
。
∵ m,n 为正整数
∴解为
3.用正三角形和正六边形铺设地面,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式是( )
A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6
D
m+2·n=6
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,则有
那么用三种正多边形:正三角形、正方形、正六边形能否进行平面铺设?如果不能铺设,为什么?如果能,你能把它画出来吗(草图)?
拓展延伸
正六边形、正方形、正三角形
正十二边形、正六边形和正方形的组合。
正十二边形、正方形、正三角形
用三种正多边形铺设的情况:
1、正三边形、正四边形和正六边形
2、正四边形、正六边形和正十二边形
3、正三边形、正四边形和正十二边形
(1×60°+ 2 ×90°+ 120° = 360°)
(1×90°+ 1×120°+1 ×150° = 360°)
(2×60°+ 1 ×90°+ 1× 120° = 360°)
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
