华东师大版七年级数学下册课件:10.1.2轴对称的再认识(共17张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册课件:10.1.2轴对称的再认识(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 386.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:43:07 | ||
图片预览





文档简介
学习目标:
1、了解线段垂直平分线角平分线及其性质。
2、会利用线段的垂直平分线性质进行简单的计算和说理。
3、正确灵活的运用垂直平分线和角平分线的性质
10.1.2轴对称的再认识
自学指导:
1、预习课本P102---P104的内容,重点理解探索线段垂直平分线性质的过程, 自己动手完成P102做一做,然后自己总结垂直平分线的概念及线段是否是轴对称图形 。
2、牢记并运用
(1)线段有且只有一条垂直平分线,有两条对称轴。
(2)角是轴对称图形,对称轴是角平分线所在的直线。角平线有如下重要的性质:角平分线上的点到角两边的距离相等。
O
A
B
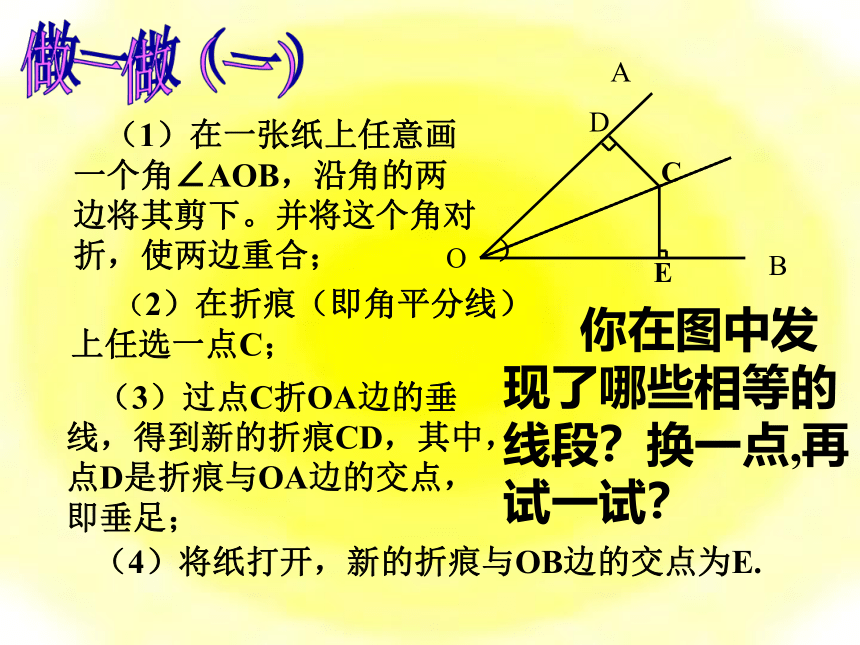
(1)在一张纸上任意画一个角∠AOB,沿角的两边将其剪下。并将这个角对折,使两边重合;
(2)在折痕(即角平分线)上任选一点C;
C
)
(3)过点C折OA边的垂线,得到新的折痕CD,其中,点D是折痕与OA边的交点,即垂足;
D
(4)将纸打开,新的折痕与OB边的交点为E.
E
你在图中发现了哪些相等的线段?换一点,再试一试?
发现:
(1)角是轴对称图形,角平分线所在直线是它的对称轴.
(2)角平分线上的点到这个角的两边的距离相等.
想一想:线段是轴对称图形吗?如果是,你能找出他的一条对称轴吗?试一试按下列步骤做一做:
(1)画一条线段AB,对折AB使点A,B重合,折痕AB的交点为O;
(2)在折痕上任取一点C,沿CA将纸折叠;
(3)把纸展开,得到折痕CA和CB
B
A(B)
O
C
★ 线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线,midperpendicular).
★ 线段垂直平分线上的点到这条线段两端点的距离相等.
对称轴
.
.
.
A1
A2
线段A1A2的中点
对称轴
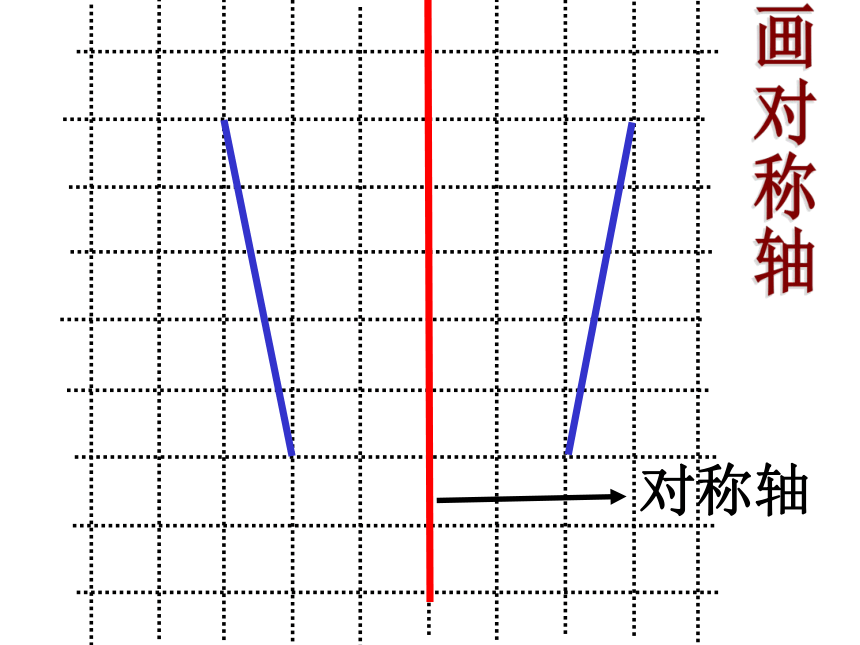
1. 画图形的对称轴的方法:
(1)找出轴对称图形的任意一组对称点;
(2)连结对称点;
(3)画出对称点所连线段的垂直平分线,
就是该图形的对称轴.
如果一个图形关于某一条直线对称,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2.轴对称性质:
3.轴对称性质的应用.
课 堂 小 结
思考:画出下列轴对称图形,做出它们的对称轴。
等腰三角形
等边三角形
正方形
长方形
Ⅰ角和线段是轴对称图形,它们的对称轴分别是角平分线所在直线和线段的垂直平分线(即中垂线);
Ⅱ角的平分线上的点到这个角的两边的距离相等;
Ⅲ线段垂直平分线上的点到 这条线段两个端点的距离相等.
1.习题10.1(第一课时) 第1,2,3,4;
2.与本节有关练习册
1:如图所示,在△ABC中,∠C= 90°,BD是角平分线, 交AC于点D, DE⊥AB, 垂足为点E, AD=3DE. AD和3DC是什么关系?为什么?
C
B
A
D
E
自学指导
解:∵∠C=∠BED=900
∠CBD=∠DBE
BD=BD
∴CD=DE
又∵AD=3DE
∴AD=3DC
1. 直线a,b,c表示三条相交叉的公路,A.B.C表示位于公路交叉处的三个村庄.若在△ABC内部修建一处加油站,使加油站到公路a ,c的距离相等,到A村与C村的距离也相等.则加油站P应修在______的角平分线与__________的中垂线的交点处.
A
B
C
c
a
b
∠B
线段AC
2.判断正误:
(1)到直线L距离相等的两点关于直线L对称 ( )
(2)两点关于连结它们的线段的中垂线对称 ( )
(3)角的两边关于该角平分线对称 ( )
(4)角平分线上点到该角两边某一点的距离相等 ( )
(5)线段中垂线上的点到该线段两点的距离相等 ( )
(6)到线段两端点距离相等的点在该线段的中垂线上
( )
(7)到角两边距离相等的点在该角的平分线上 ( )
X
√
√
X
X
√
√
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,P D⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
(2) 如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
图(2)
如图,AB是△ABC的一条边,,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=______cm,
DA= _cm.
A
B
E
D
C
图(1)
4
6
26
1、了解线段垂直平分线角平分线及其性质。
2、会利用线段的垂直平分线性质进行简单的计算和说理。
3、正确灵活的运用垂直平分线和角平分线的性质
10.1.2轴对称的再认识
自学指导:
1、预习课本P102---P104的内容,重点理解探索线段垂直平分线性质的过程, 自己动手完成P102做一做,然后自己总结垂直平分线的概念及线段是否是轴对称图形 。
2、牢记并运用
(1)线段有且只有一条垂直平分线,有两条对称轴。
(2)角是轴对称图形,对称轴是角平分线所在的直线。角平线有如下重要的性质:角平分线上的点到角两边的距离相等。
O
A
B
(1)在一张纸上任意画一个角∠AOB,沿角的两边将其剪下。并将这个角对折,使两边重合;
(2)在折痕(即角平分线)上任选一点C;
C
)
(3)过点C折OA边的垂线,得到新的折痕CD,其中,点D是折痕与OA边的交点,即垂足;
D
(4)将纸打开,新的折痕与OB边的交点为E.
E
你在图中发现了哪些相等的线段?换一点,再试一试?
发现:
(1)角是轴对称图形,角平分线所在直线是它的对称轴.
(2)角平分线上的点到这个角的两边的距离相等.
想一想:线段是轴对称图形吗?如果是,你能找出他的一条对称轴吗?试一试按下列步骤做一做:
(1)画一条线段AB,对折AB使点A,B重合,折痕AB的交点为O;
(2)在折痕上任取一点C,沿CA将纸折叠;
(3)把纸展开,得到折痕CA和CB
B
A(B)
O
C
★ 线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线,midperpendicular).
★ 线段垂直平分线上的点到这条线段两端点的距离相等.
对称轴
.
.
.
A1
A2
线段A1A2的中点
对称轴
1. 画图形的对称轴的方法:
(1)找出轴对称图形的任意一组对称点;
(2)连结对称点;
(3)画出对称点所连线段的垂直平分线,
就是该图形的对称轴.
如果一个图形关于某一条直线对称,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2.轴对称性质:
3.轴对称性质的应用.
课 堂 小 结
思考:画出下列轴对称图形,做出它们的对称轴。
等腰三角形
等边三角形
正方形
长方形
Ⅰ角和线段是轴对称图形,它们的对称轴分别是角平分线所在直线和线段的垂直平分线(即中垂线);
Ⅱ角的平分线上的点到这个角的两边的距离相等;
Ⅲ线段垂直平分线上的点到 这条线段两个端点的距离相等.
1.习题10.1(第一课时) 第1,2,3,4;
2.与本节有关练习册
1:如图所示,在△ABC中,∠C= 90°,BD是角平分线, 交AC于点D, DE⊥AB, 垂足为点E, AD=3DE. AD和3DC是什么关系?为什么?
C
B
A
D
E
自学指导
解:∵∠C=∠BED=900
∠CBD=∠DBE
BD=BD
∴CD=DE
又∵AD=3DE
∴AD=3DC
1. 直线a,b,c表示三条相交叉的公路,A.B.C表示位于公路交叉处的三个村庄.若在△ABC内部修建一处加油站,使加油站到公路a ,c的距离相等,到A村与C村的距离也相等.则加油站P应修在______的角平分线与__________的中垂线的交点处.
A
B
C
c
a
b
∠B
线段AC
2.判断正误:
(1)到直线L距离相等的两点关于直线L对称 ( )
(2)两点关于连结它们的线段的中垂线对称 ( )
(3)角的两边关于该角平分线对称 ( )
(4)角平分线上点到该角两边某一点的距离相等 ( )
(5)线段中垂线上的点到该线段两点的距离相等 ( )
(6)到线段两端点距离相等的点在该线段的中垂线上
( )
(7)到角两边距离相等的点在该角的平分线上 ( )
X
√
√
X
X
√
√
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,P D⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
(2) 如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
图(2)
如图,AB是△ABC的一条边,,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=______cm,
DA= _cm.
A
B
E
D
C
图(1)
4
6
26
