华东师大版七年级数学下册课件:10.2.2平移的特征(共30张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册课件:10.2.2平移的特征(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览







文档简介
学 习 目 标
1、回顾平移的定义。
2、能找出平移的对应点、对应边、对应角。
3、能找出平移方向和平移距离。
4、感悟一些数学思想方法:运动变化思想、.化归思想 。
回顾
(1)平移的定义
在平面内,将一个图形沿某个方向平行移动一定的距离,这样的图形运动称为平移。
(2)平移的特点
经平移运动后的图形: 形状和大小不变,图形的位置发生变化.
1. 什么叫平移?平移有何特点?
2. 平移是由什么决定的?
由移动的方向和移动的距离所决定.
3. 要求
1.会判断是否是平移图形;
2.能够找出平移图形的对应点对应线段和对应角.
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A?
B?
C?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A
B
C
0
2
1
3
4
5
6
7
8
9
10
P
Q
A
B
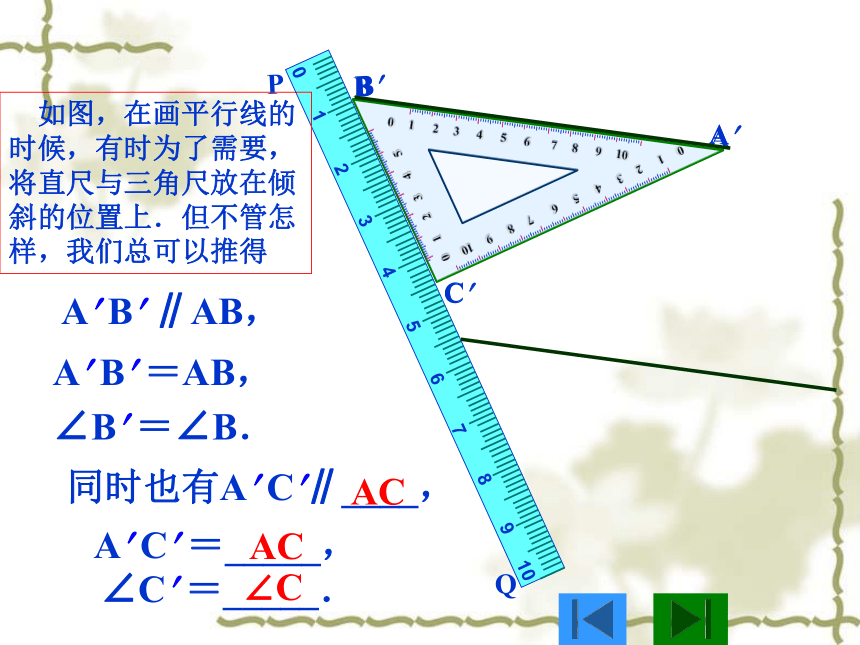
A? B? ∥AB,
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.但不管怎样,我们总可以推得
A? B? =AB,
∠B? =∠B.
同时也有A? C?∥____,
A? C? =_____,
∠C? =_____.
AC
AC
∠C
这就告诉我们,平移后的图形与原来的图形的对应线段平行并且相等,对应角相等,图形的形状与大小都没有发生变化.
注 意
在平移过程中,对应线段也可能在一条直线上(如上图中的B? C?与BC).
探索
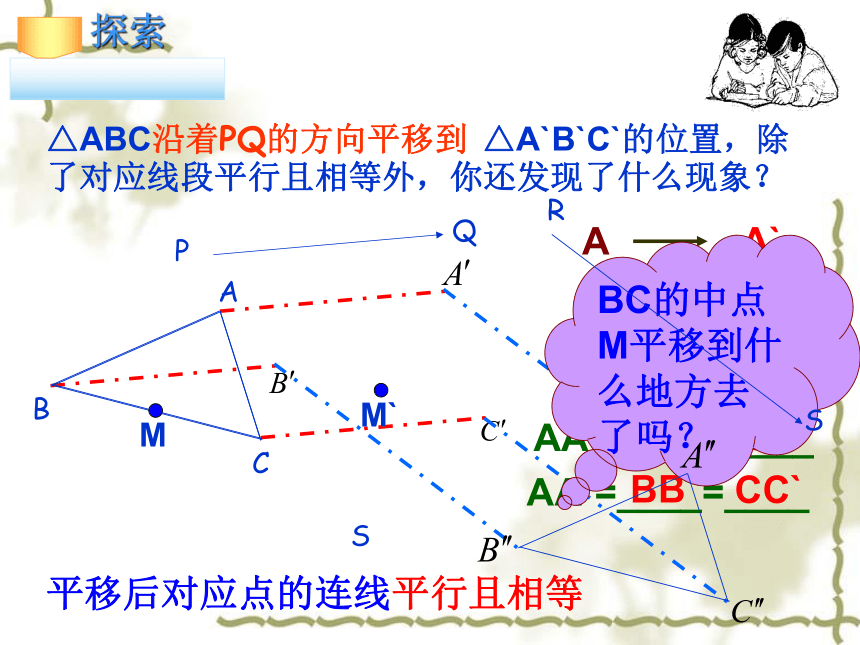
△ABC沿着PQ的方向平移到 △A`B`C`的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A`
B
B`
C
C`
AA`//____//____
AA`=____=____
BB`
CC`
CC`
BB`
平移后对应点的连线平行且相等
BC的中点M平移到什么地方去了吗?
M
M`
S
R
S
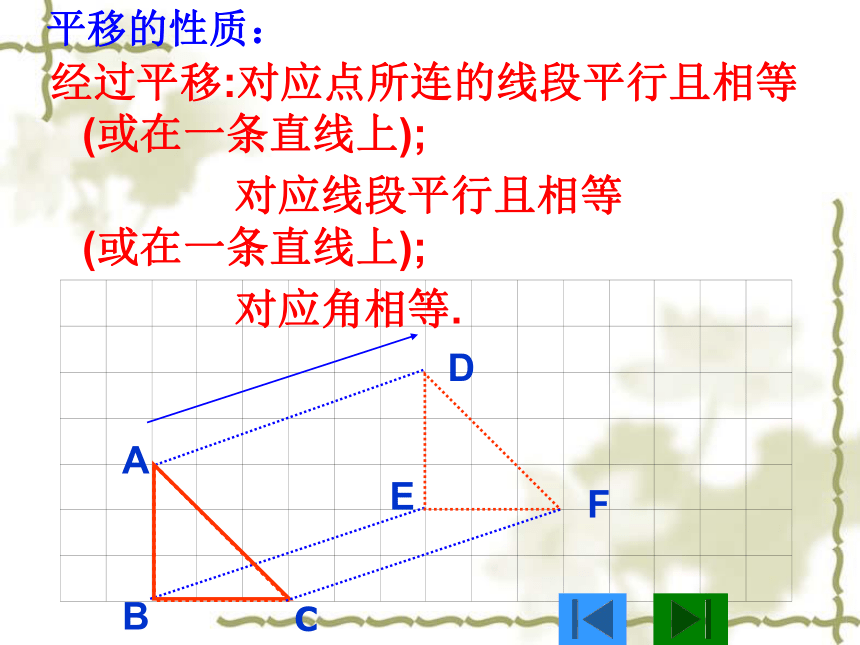
平移的性质:
经过平移:对应点所连的线段平行且相等 (或在一条直线上);
对应线段平行且相等 (或在一条直线上);
对应角相等.
A
B
D
E
F
C
A?
B?
C?
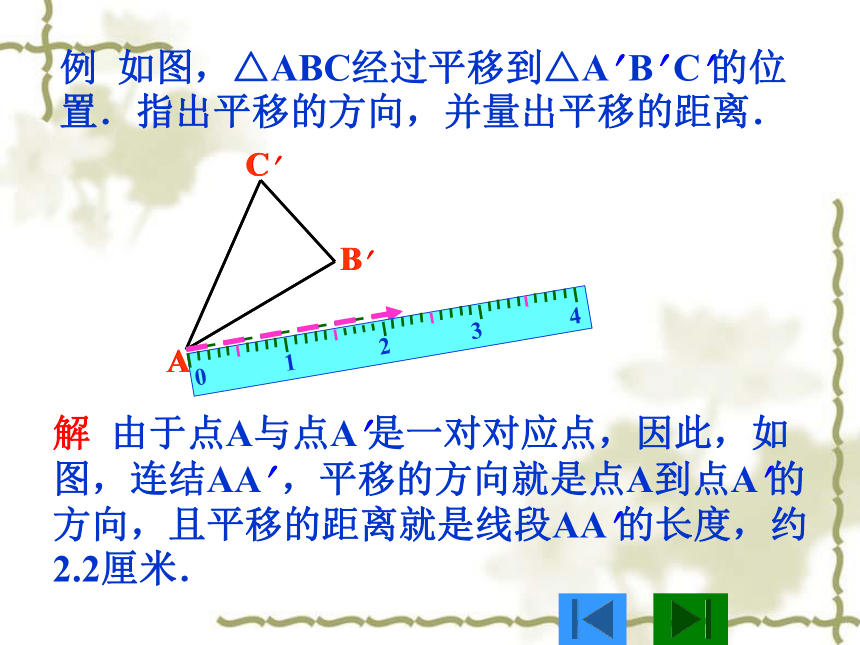
例 如图,△ABC经过平移到△A? B? C?的位置.指出平移的方向,并量出平移的距离.
解 由于点A与点A?是一对对应点,因此,如图,连结AA? ,平移的方向就是点A到点A?的方向,且平移的距离就是线段AA?的长度,约2.2厘米.
A
B
C
0
2
4
3
1
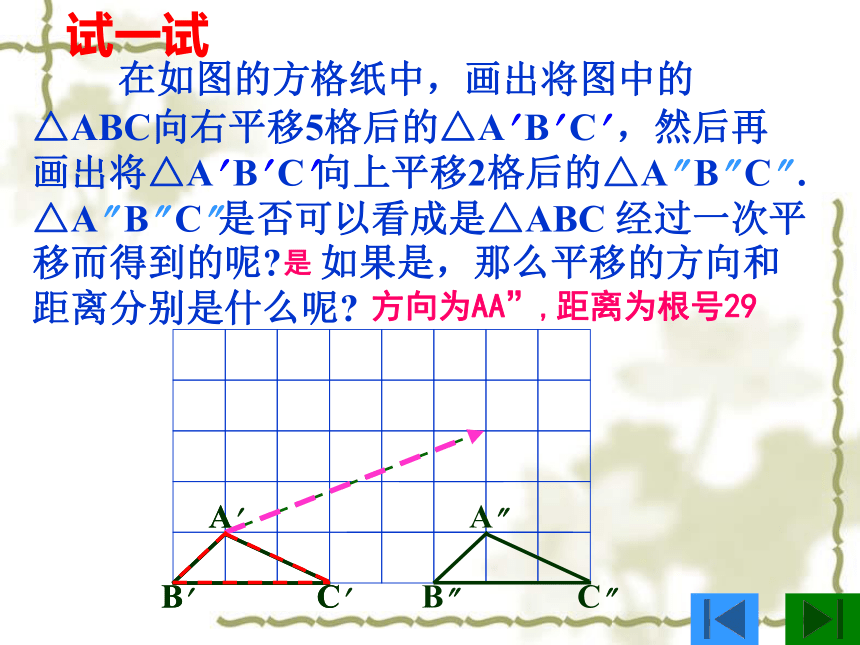
在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A? B? C? ,然后再画出将△A? B? C?向上平移2格后的△A? B? C? . △A? B? C?是否可以看成是△ABC 经过一次平移而得到的呢? 如果是,那么平移的方向和距离分别是什么呢?
试一试
A
B
C
A?
B?
C?
A?
B?
C?
是
方向为AA”,距离为根号29
C?
做一做
如图,在纸上画△ABC和两条平行的对称轴m、 n.画出△ABC关于直线m对称的△A? B? C? ,再画出△A? B? C?关于直线n对称的△A? B? C? .
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?
A
B
C
m
n
A?
B?
A?
B?
C?
互相平移得到的,即两次翻折(对称轴要互相平行)相当于一次平移.
平移的特征
(1)经平移运动后的图形: 形状和大小不变,图形的位置发生变化.
小结 :
(2)平移后的图形与原来的图形的对应线段平行并且相等(或在一条直线上),对应点所连的线段平行并且相等(或在一条直线上),对应角相等.
练习
1. 如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长.
A
B
C
D
O
(A? )
(B? )
(O? )
2. 先将方格纸中的图形向左平移5格,然后再向下平移3格.
3. 将所给图形沿着PQ方向平移,平移的距离为线段PQ的长.画出平移后的新图形.
P
Q
1.平移改变的是图形的 ( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2.经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同
B 既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
选择
A
C
A
B
C
D
E
F
练习1 如图,△ABC平移之后到了△DEF的位置,下列说法错误的是(???? )
A 点B的对应点是点E
B 平移的距离是线段BE 的长度
C 点A的对应点是点B
D 点C的对应点是点F
C
练习2 已知△ABD沿BD平移到了△FCE的位置,CE=10,CD=4,则平移的方向是____________,平移的距离是 _____.
B
D
A
C
E
F
沿射线BD的方向
6
如图,∠DEF是∠ABC经过平移得到的,∠ABC=33?,求∠DEF的度数.
A
B
C
D
E
F
随堂练习1
∠DEF=33度
F
A
B
C
E
D
2.图中的4个小三角形都是等边三角形,边长为1.3 cm,你能通过平移三角形ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
答: ?ABC沿射线BF和射线BD的方向平移1.3cm,可以分别得到?FAE和?ECD.
如图:直线a与直线b平行.
a
b
.
.
.
C
C?
A
A?
(1)在直线a上任意取两点A、A?,分别过点A、A?作直线b的垂线,垂足分别为C、C? .
(2)分别度量点A、A?到直线b的距离,你发现了什么?
AC=A? C?
如图:直线a与直线b不平行.
(1)在直线a上任意取两点A、A?,分别过点A、A?作直线b的垂线,垂足分别为C、C? .
a
b
.
.
.
C
C?
A
A?
(2)分别度量点A、A?到直线b的距离,你发现了什么?
AC A? C?
如果两条直线互相平行,那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离.
a
b
.
.
A
A?
例:
已知△ABC中,AB=AC,AD是BC边上的高,画出△ABD平移后的三角形。其平移方向为射线BD,平移的距离为线段BD的长
A
B
C
D
北
东
A
B
C
O
30?
5cm
将三角形ABC沿南偏东30?方向平移5cm
2.如图,将字母M按箭头所指的方向平移3cm,作出平移后的图形.
任意画一个三角形,然后将此三角形沿着北偏东60°的方向平移2.8厘米,画出平移后的三角形.
2. 平移方格纸中的图形(如图),使点A平移到点A′处,画出平移后的图形.
(第2题) (第3题)
3. 如图,AB=DC,画出线段AB平移后的线段DE,其平移方向为射线AD的方向,平移的距离为线段AD的长.平移后所得的线段DE与线段DC相等吗?连结EC, ∠DEC与∠DCE相等吗?试说明理由.
(由平移的性质知AB=DE,而AB=DC,所以DE=DC;因为在⊿DEC中,DE=DC,所以∠DEC=∠DCD.)
4. 利用如图所示的图形,通过平移设计图案.
(第4题)
1、回顾平移的定义。
2、能找出平移的对应点、对应边、对应角。
3、能找出平移方向和平移距离。
4、感悟一些数学思想方法:运动变化思想、.化归思想 。
回顾
(1)平移的定义
在平面内,将一个图形沿某个方向平行移动一定的距离,这样的图形运动称为平移。
(2)平移的特点
经平移运动后的图形: 形状和大小不变,图形的位置发生变化.
1. 什么叫平移?平移有何特点?
2. 平移是由什么决定的?
由移动的方向和移动的距离所决定.
3. 要求
1.会判断是否是平移图形;
2.能够找出平移图形的对应点对应线段和对应角.
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A?
B?
C?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A
B
C
0
2
1
3
4
5
6
7
8
9
10
P
Q
A
B
A? B? ∥AB,
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.但不管怎样,我们总可以推得
A? B? =AB,
∠B? =∠B.
同时也有A? C?∥____,
A? C? =_____,
∠C? =_____.
AC
AC
∠C
这就告诉我们,平移后的图形与原来的图形的对应线段平行并且相等,对应角相等,图形的形状与大小都没有发生变化.
注 意
在平移过程中,对应线段也可能在一条直线上(如上图中的B? C?与BC).
探索
△ABC沿着PQ的方向平移到 △A`B`C`的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A`
B
B`
C
C`
AA`//____//____
AA`=____=____
BB`
CC`
CC`
BB`
平移后对应点的连线平行且相等
BC的中点M平移到什么地方去了吗?
M
M`
S
R
S
平移的性质:
经过平移:对应点所连的线段平行且相等 (或在一条直线上);
对应线段平行且相等 (或在一条直线上);
对应角相等.
A
B
D
E
F
C
A?
B?
C?
例 如图,△ABC经过平移到△A? B? C?的位置.指出平移的方向,并量出平移的距离.
解 由于点A与点A?是一对对应点,因此,如图,连结AA? ,平移的方向就是点A到点A?的方向,且平移的距离就是线段AA?的长度,约2.2厘米.
A
B
C
0
2
4
3
1
在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A? B? C? ,然后再画出将△A? B? C?向上平移2格后的△A? B? C? . △A? B? C?是否可以看成是△ABC 经过一次平移而得到的呢? 如果是,那么平移的方向和距离分别是什么呢?
试一试
A
B
C
A?
B?
C?
A?
B?
C?
是
方向为AA”,距离为根号29
C?
做一做
如图,在纸上画△ABC和两条平行的对称轴m、 n.画出△ABC关于直线m对称的△A? B? C? ,再画出△A? B? C?关于直线n对称的△A? B? C? .
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?
A
B
C
m
n
A?
B?
A?
B?
C?
互相平移得到的,即两次翻折(对称轴要互相平行)相当于一次平移.
平移的特征
(1)经平移运动后的图形: 形状和大小不变,图形的位置发生变化.
小结 :
(2)平移后的图形与原来的图形的对应线段平行并且相等(或在一条直线上),对应点所连的线段平行并且相等(或在一条直线上),对应角相等.
练习
1. 如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长.
A
B
C
D
O
(A? )
(B? )
(O? )
2. 先将方格纸中的图形向左平移5格,然后再向下平移3格.
3. 将所给图形沿着PQ方向平移,平移的距离为线段PQ的长.画出平移后的新图形.
P
Q
1.平移改变的是图形的 ( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2.经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同
B 既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
选择
A
C
A
B
C
D
E
F
练习1 如图,△ABC平移之后到了△DEF的位置,下列说法错误的是(???? )
A 点B的对应点是点E
B 平移的距离是线段BE 的长度
C 点A的对应点是点B
D 点C的对应点是点F
C
练习2 已知△ABD沿BD平移到了△FCE的位置,CE=10,CD=4,则平移的方向是____________,平移的距离是 _____.
B
D
A
C
E
F
沿射线BD的方向
6
如图,∠DEF是∠ABC经过平移得到的,∠ABC=33?,求∠DEF的度数.
A
B
C
D
E
F
随堂练习1
∠DEF=33度
F
A
B
C
E
D
2.图中的4个小三角形都是等边三角形,边长为1.3 cm,你能通过平移三角形ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
答: ?ABC沿射线BF和射线BD的方向平移1.3cm,可以分别得到?FAE和?ECD.
如图:直线a与直线b平行.
a
b
.
.
.
C
C?
A
A?
(1)在直线a上任意取两点A、A?,分别过点A、A?作直线b的垂线,垂足分别为C、C? .
(2)分别度量点A、A?到直线b的距离,你发现了什么?
AC=A? C?
如图:直线a与直线b不平行.
(1)在直线a上任意取两点A、A?,分别过点A、A?作直线b的垂线,垂足分别为C、C? .
a
b
.
.
.
C
C?
A
A?
(2)分别度量点A、A?到直线b的距离,你发现了什么?
AC A? C?
如果两条直线互相平行,那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离.
a
b
.
.
A
A?
例:
已知△ABC中,AB=AC,AD是BC边上的高,画出△ABD平移后的三角形。其平移方向为射线BD,平移的距离为线段BD的长
A
B
C
D
北
东
A
B
C
O
30?
5cm
将三角形ABC沿南偏东30?方向平移5cm
2.如图,将字母M按箭头所指的方向平移3cm,作出平移后的图形.
任意画一个三角形,然后将此三角形沿着北偏东60°的方向平移2.8厘米,画出平移后的三角形.
2. 平移方格纸中的图形(如图),使点A平移到点A′处,画出平移后的图形.
(第2题) (第3题)
3. 如图,AB=DC,画出线段AB平移后的线段DE,其平移方向为射线AD的方向,平移的距离为线段AD的长.平移后所得的线段DE与线段DC相等吗?连结EC, ∠DEC与∠DCE相等吗?试说明理由.
(由平移的性质知AB=DE,而AB=DC,所以DE=DC;因为在⊿DEC中,DE=DC,所以∠DEC=∠DCD.)
4. 利用如图所示的图形,通过平移设计图案.
(第4题)
