华东师大版七年级数学下册课件:第9章《多边形》复习(共15张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册课件:第9章《多边形》复习(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:50:41 | ||
图片预览




文档简介
第九章 多边形
回顾与思考
1、概念:由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
三角形的概念及分类
2、分类:
按角分
锐角三角形
直角三角形
钝角三角形
按边分
等腰三角形
斜三角形
不等边三角形(不规则三角形)
只有两条边相等的等腰三角形
等边三角形
三角形的高、中线、角平分线
锐角三角形的高都在三角形的内部,
且交于一点
直角三角形的三条高交于直角顶点
钝角三角形的三条高不交于一点,
但它们所在直线交于一点
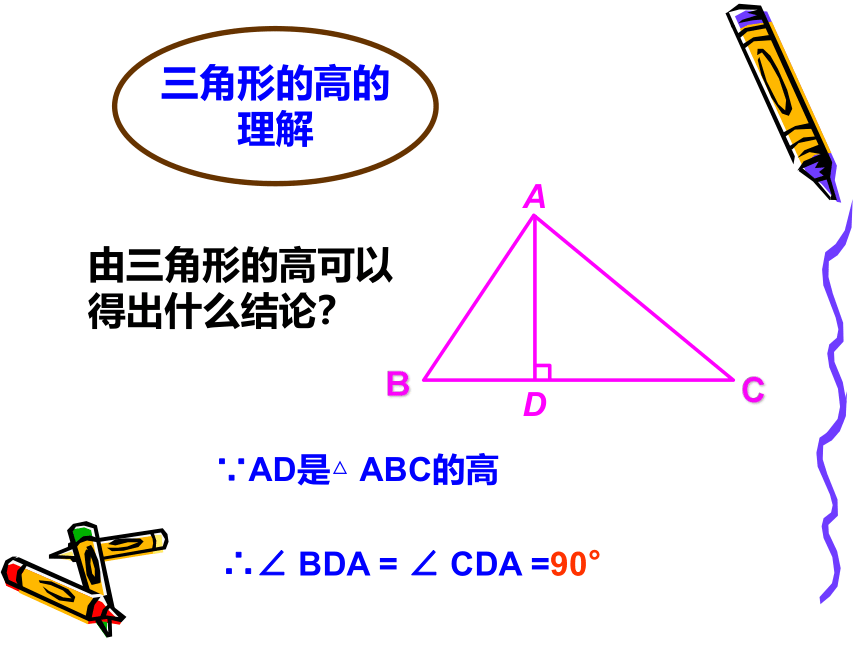
三角形的高
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
三角形的高的
理解
由三角形的高可以得出什么结论?
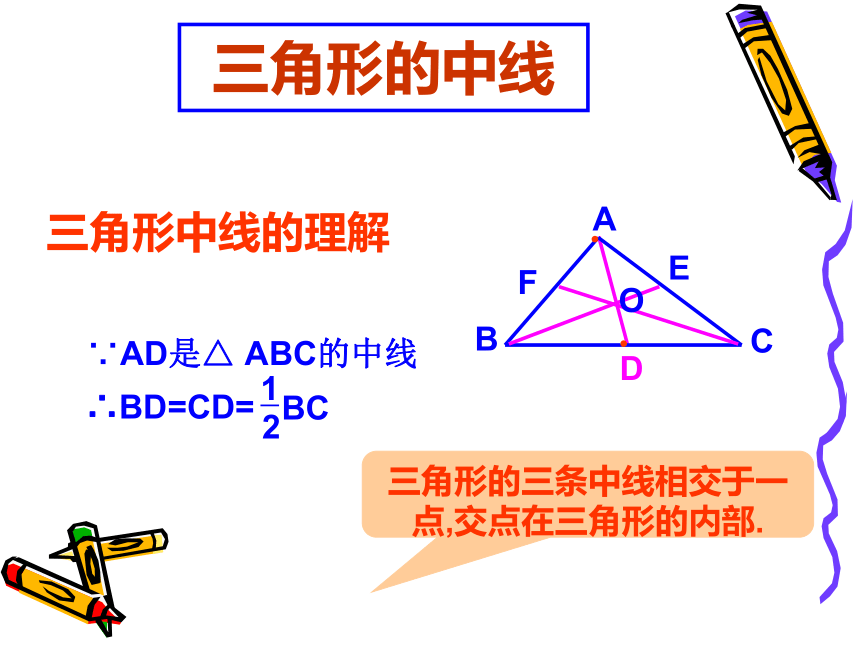
三角形的中线
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD=
1
2
BC
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的理解
E
F
O
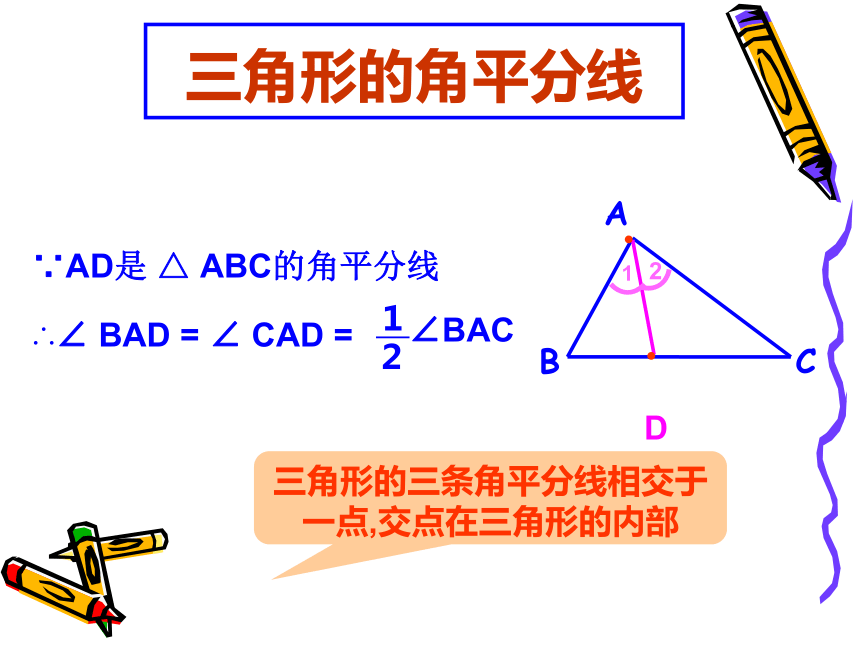
三角形的角平分线
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ BAD = ∠ CAD =
1
2
∠BAC
●
●
三角形的三条角平分线相交于一点,交点在三角形的内部
︶
︶
1
2
练习
填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
AF
CD
AC
∠2
∠ABC
∠4
三角形的内角和与外角和
三角形的外角和等于3600
三角形的内角和等于1800
∠ACD= ∠A+ ∠B
(1)三角形的一个外角等于与它不相邻的两个
内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
∠ACD > ∠A
∠ACD > ∠B
三角形外角的性质
已知三角形两边a、b长为 9、5,
则第三边c的取值范围 。
三角形的任何两边之差小于第三边。
|a-b|< c<a+b
三角形的任何两边之和大于第三边。
三角形的三边关系
在建筑工地我们常可看见如图所示,用
木条EF固定矩形门框ABCD的情形。这种做
法根据( )
A、两点之间线段最短
B、两点确定一条直线
C、三角形的稳定性
D、矩形的四个角都是直角
C
多边形的内角和与外角和
1、n边形的内角和公式:(n-2)×180°
2、多边形的外角和是360°
如图所示, △ABC的高BD、CE交于H点,
∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
返回
下一页
上一页
用同种正多边形瓷砖能不留空隙,不重叠地铺满
地板的关键是:
围绕一点拼在一起的正多边形的几个内角之和为360?
模型:
正多边形个数×正多边形每个内角度数=360?
两种正多边形拼地板:
围绕 一点拼在一起的两种正多边形的
内角之和为360?。
关键:
模型:
正多边形1个数×正多边形1内角度数 +
正多边形2个数×正多边形2内角度数=360 ?
及时检测
某装修公司到科维商场买同样一种多边形的地砖平铺地面,在以下四种地砖中,你认为该公司不能买( )
A.正三角形地砖 B.正方形地砖
C.正五边形地砖 D.正六边形地砖
回顾与思考
1、概念:由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
三角形的概念及分类
2、分类:
按角分
锐角三角形
直角三角形
钝角三角形
按边分
等腰三角形
斜三角形
不等边三角形(不规则三角形)
只有两条边相等的等腰三角形
等边三角形
三角形的高、中线、角平分线
锐角三角形的高都在三角形的内部,
且交于一点
直角三角形的三条高交于直角顶点
钝角三角形的三条高不交于一点,
但它们所在直线交于一点
三角形的高
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
三角形的高的
理解
由三角形的高可以得出什么结论?
三角形的中线
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD=
1
2
BC
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的理解
E
F
O
三角形的角平分线
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ BAD = ∠ CAD =
1
2
∠BAC
●
●
三角形的三条角平分线相交于一点,交点在三角形的内部
︶
︶
1
2
练习
填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
AF
CD
AC
∠2
∠ABC
∠4
三角形的内角和与外角和
三角形的外角和等于3600
三角形的内角和等于1800
∠ACD= ∠A+ ∠B
(1)三角形的一个外角等于与它不相邻的两个
内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
∠ACD > ∠A
∠ACD > ∠B
三角形外角的性质
已知三角形两边a、b长为 9、5,
则第三边c的取值范围 。
三角形的任何两边之差小于第三边。
|a-b|< c<a+b
三角形的任何两边之和大于第三边。
三角形的三边关系
在建筑工地我们常可看见如图所示,用
木条EF固定矩形门框ABCD的情形。这种做
法根据( )
A、两点之间线段最短
B、两点确定一条直线
C、三角形的稳定性
D、矩形的四个角都是直角
C
多边形的内角和与外角和
1、n边形的内角和公式:(n-2)×180°
2、多边形的外角和是360°
如图所示, △ABC的高BD、CE交于H点,
∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
返回
下一页
上一页
用同种正多边形瓷砖能不留空隙,不重叠地铺满
地板的关键是:
围绕一点拼在一起的正多边形的几个内角之和为360?
模型:
正多边形个数×正多边形每个内角度数=360?
两种正多边形拼地板:
围绕 一点拼在一起的两种正多边形的
内角之和为360?。
关键:
模型:
正多边形1个数×正多边形1内角度数 +
正多边形2个数×正多边形2内角度数=360 ?
及时检测
某装修公司到科维商场买同样一种多边形的地砖平铺地面,在以下四种地砖中,你认为该公司不能买( )
A.正三角形地砖 B.正方形地砖
C.正五边形地砖 D.正六边形地砖
