华师版八年级数学下册课件:18.1.1-平行四边形的性质(第1课时)(25张PPT)
文档属性
| 名称 | 华师版八年级数学下册课件:18.1.1-平行四边形的性质(第1课时)(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览





文档简介
18.1.1 平行四边形的性质
(边、角性质)
(1)、理解平行四边形的概念,了解四边形的不稳定性。?
(2)、探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等。??
学习目标
(1)重点:平行四边形性质的探究和应用。
(2)难点:平行四边形的性质定理的证明及应用。?
请同学们欣赏一组日常生活中常见的图片,你能观察到图片中有我们学过的哪些四边形?
1.定义:
有两组对边分别平行的四边形叫做平行四边形.
2.记作:
A
B
D
C
□ABCD
3.读作:
5.对边:AB、CD; AD、BC.
对角:
4.几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
平行四边形ABCD
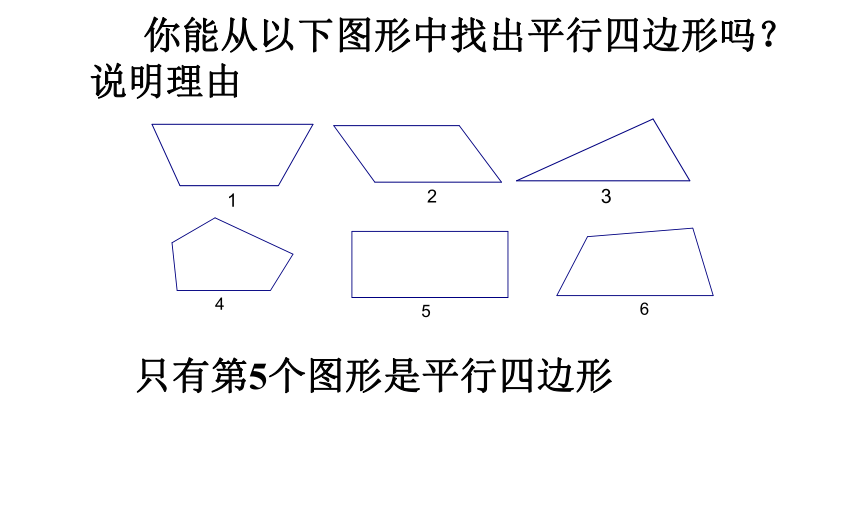
你能从以下图形中找出平行四边形吗?说明理由
只有第5个图形是平行四边形
(1)要识别一个图形是 平行四边形,目前的方法有几个?
(2)平行四边形首先应该是几边形?
(3)应该有几组对边平行?
思考:
概括:定义既是性质也是判定方法,现在判定一个四边形是平行四边形的方法只有一个,就是利用定义判定
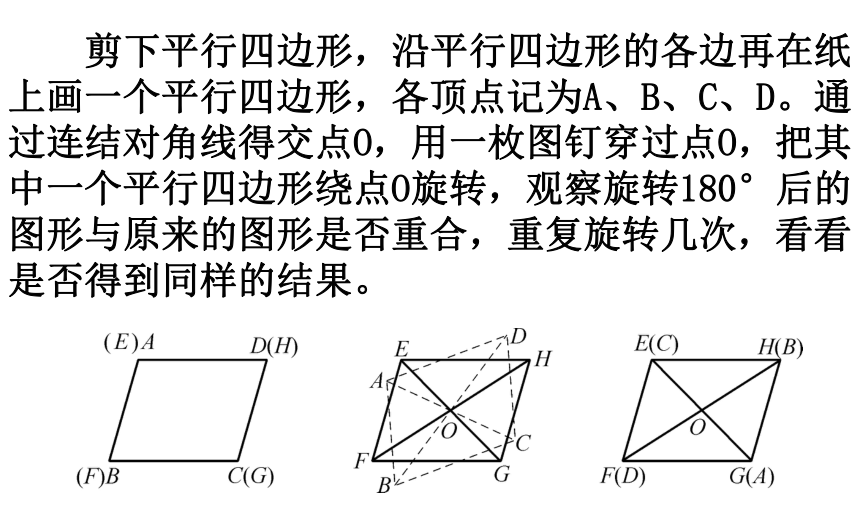
剪下平行四边形,沿平行四边形的各边再在纸上画一个平行四边形,各顶点记为A、B、C、D。通过连结对角线得交点O,用一枚图钉穿过点O,把其中一个平行四边形绕点O旋转,观察旋转180°后的图形与原来的图形是否重合,重复旋转几次,看看是否得到同样的结果。
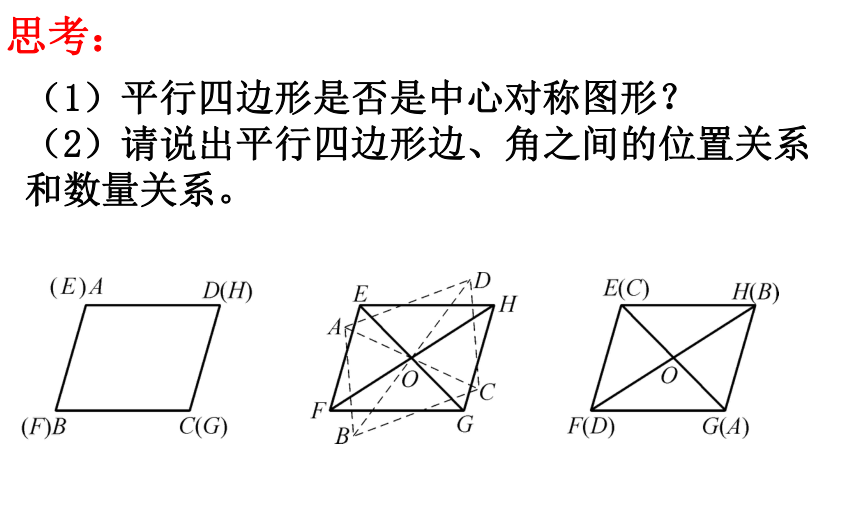
(1)平行四边形是否是中心对称图形?
(2)请说出平行四边形边、角之间的位置关系和数量关系。
思考:
D
C
A
B
2
3
1
4
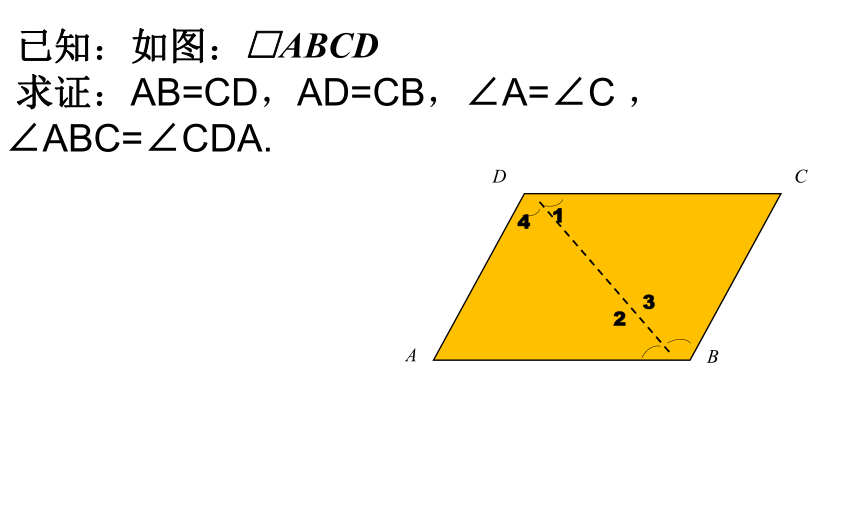
已知:如图:
求证:AB=CD,AD=CB,∠A=∠C ,∠ABC=∠CDA.
□ABCD
D
C
A
B
2
3
1
4
证明:连结 BD .
∵四边形 ABCD 是平行四边形 ,
∴AB//DC ,AD//BC
∴∠2=∠1 , ∠4 =∠3 .
又∵BD = DB ,
∴△ABD≌△CBD .
∴AB = CD ,AD = CB , ∠A = ∠C
由∠2=∠1 , ∠4 =∠3 得
∠2 + ∠3 = ∠1+∠4 ,
即∠ABC=∠CDA .
归纳:平行四边形的问题可以转化为三角形的问题解决。
D
C
A
B
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
A
B
D
C
例1 如图,在 中,已知∠A=40°,
求其他各个内角的度数;
□ABCD
A
B
D
C
例1 如图,在 中,已知∠A=40°,
求其他各个内角的度数;
□ABCD
解:在 中,
∠A = ∠C,∠B= ∠D ∵∠A=40°,
∴∠C=40°.
又∵AD∥BC,
∴∠A +∠B =180°,
∴∠B=180°- ∠A
=180°-140° = 140° ∴∠D=∠B=140°
□ABCD
1、将例1中的∠A=40°改为∠B=140°求
各个内角的度数
□ABCD
变式训练
A
B
D
C
解:在 中,
∠A = ∠C,∠B= ∠D ∵∠B=140°,
∴∠D=140°.
又∵AD∥BC,
∴∠A +∠B =180°,
∴∠A=180°- ∠B
=180°-140° = 40° ∴∠A = ∠C= 40°
□ABCD
2、如图,在 中,已知AC平分∠BAD,∠BAC=20°,求各内角的度数。
□ABCD
变式训练
解:在 中,
∠B = ∠D,∠BAD= ∠BCD ∵AC平分∠BAD,∠BAC=20°
∴∠BAD=∠BCD=2∠BAC=40°.
又∵AD∥BC,
∴∠BAD +∠B =180°,
∴∠B=180°-∠BAD=180°-40° = 140° ∴∠B = ∠D= 140°
□ABCD
例2、如图, 中,已知AB=8,周长达24,求其余三边的长。
□ABCD
例2、如图, 中,已知AB=8,周长达24,求其余三边的长。
□ABCD
解:在
∴AB = DC,AD=BC
∵AB=8,
∴DC=8,
又∵ AB+BC+CD+DA=24,
∴ AD=BC=4
□ABCD中
□ABCD
练习一:填空题
1、在 中,∠A=72°, 则∠B=_____°,
∠C= ______ °, ∠D= _____° ;
2、在 中 ,若∠A+ ∠C= 210°,则∠A=______ 、∠B=______
3、在 中, AB+CD=28cm. 的周长
等于96cm, 则AB=______, BC=______ ,
CD=______ , AD=______ .
□ABCD
□ABCD
□ABCD
108
108
72
105°
75°
14
34
14
34
A
B
D
C
练习二 如图, 中,∠A=3∠B, 求∠C和∠D 的度数
□ABCD
解:∵四边形ABCD是平行四边形
∴∠A = ∠C,∠B= ∠D
AD∥BC
∴∠A +∠B =180°
∵∠A=3∠B
∴∠B=45°∠A=135°
∴∠A = ∠C=135°
∠B= ∠D=45°
练习三:已知 的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
□ABCD
解:在 中,
AB =CD,BC= AD ∵ 的周长为60cm
∴AB+CD+BC+AD=60
即AB+BC=30
又∵AB:BC=3:2
□ABCD
□ABCD
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
练一练
5.5cm
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在 中,如果∠A=42°那么∠B=48° ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠C=145°. ( )
□ABCD
练一练
5.5cm
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在 中,如果∠A=42°那么∠B=48° ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠C=145°. ( )
√
√
×
□ABCD
√
×
×
课堂小结:
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
3. 两平行线的距离相等
(边、角性质)
(1)、理解平行四边形的概念,了解四边形的不稳定性。?
(2)、探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等。??
学习目标
(1)重点:平行四边形性质的探究和应用。
(2)难点:平行四边形的性质定理的证明及应用。?
请同学们欣赏一组日常生活中常见的图片,你能观察到图片中有我们学过的哪些四边形?
1.定义:
有两组对边分别平行的四边形叫做平行四边形.
2.记作:
A
B
D
C
□ABCD
3.读作:
5.对边:AB、CD; AD、BC.
对角:
4.几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
平行四边形ABCD
你能从以下图形中找出平行四边形吗?说明理由
只有第5个图形是平行四边形
(1)要识别一个图形是 平行四边形,目前的方法有几个?
(2)平行四边形首先应该是几边形?
(3)应该有几组对边平行?
思考:
概括:定义既是性质也是判定方法,现在判定一个四边形是平行四边形的方法只有一个,就是利用定义判定
剪下平行四边形,沿平行四边形的各边再在纸上画一个平行四边形,各顶点记为A、B、C、D。通过连结对角线得交点O,用一枚图钉穿过点O,把其中一个平行四边形绕点O旋转,观察旋转180°后的图形与原来的图形是否重合,重复旋转几次,看看是否得到同样的结果。
(1)平行四边形是否是中心对称图形?
(2)请说出平行四边形边、角之间的位置关系和数量关系。
思考:
D
C
A
B
2
3
1
4
已知:如图:
求证:AB=CD,AD=CB,∠A=∠C ,∠ABC=∠CDA.
□ABCD
D
C
A
B
2
3
1
4
证明:连结 BD .
∵四边形 ABCD 是平行四边形 ,
∴AB//DC ,AD//BC
∴∠2=∠1 , ∠4 =∠3 .
又∵BD = DB ,
∴△ABD≌△CBD .
∴AB = CD ,AD = CB , ∠A = ∠C
由∠2=∠1 , ∠4 =∠3 得
∠2 + ∠3 = ∠1+∠4 ,
即∠ABC=∠CDA .
归纳:平行四边形的问题可以转化为三角形的问题解决。
D
C
A
B
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
A
B
D
C
例1 如图,在 中,已知∠A=40°,
求其他各个内角的度数;
□ABCD
A
B
D
C
例1 如图,在 中,已知∠A=40°,
求其他各个内角的度数;
□ABCD
解:在 中,
∠A = ∠C,∠B= ∠D ∵∠A=40°,
∴∠C=40°.
又∵AD∥BC,
∴∠A +∠B =180°,
∴∠B=180°- ∠A
=180°-140° = 140° ∴∠D=∠B=140°
□ABCD
1、将例1中的∠A=40°改为∠B=140°求
各个内角的度数
□ABCD
变式训练
A
B
D
C
解:在 中,
∠A = ∠C,∠B= ∠D ∵∠B=140°,
∴∠D=140°.
又∵AD∥BC,
∴∠A +∠B =180°,
∴∠A=180°- ∠B
=180°-140° = 40° ∴∠A = ∠C= 40°
□ABCD
2、如图,在 中,已知AC平分∠BAD,∠BAC=20°,求各内角的度数。
□ABCD
变式训练
解:在 中,
∠B = ∠D,∠BAD= ∠BCD ∵AC平分∠BAD,∠BAC=20°
∴∠BAD=∠BCD=2∠BAC=40°.
又∵AD∥BC,
∴∠BAD +∠B =180°,
∴∠B=180°-∠BAD=180°-40° = 140° ∴∠B = ∠D= 140°
□ABCD
例2、如图, 中,已知AB=8,周长达24,求其余三边的长。
□ABCD
例2、如图, 中,已知AB=8,周长达24,求其余三边的长。
□ABCD
解:在
∴AB = DC,AD=BC
∵AB=8,
∴DC=8,
又∵ AB+BC+CD+DA=24,
∴ AD=BC=4
□ABCD中
□ABCD
练习一:填空题
1、在 中,∠A=72°, 则∠B=_____°,
∠C= ______ °, ∠D= _____° ;
2、在 中 ,若∠A+ ∠C= 210°,则∠A=______ 、∠B=______
3、在 中, AB+CD=28cm. 的周长
等于96cm, 则AB=______, BC=______ ,
CD=______ , AD=______ .
□ABCD
□ABCD
□ABCD
108
108
72
105°
75°
14
34
14
34
A
B
D
C
练习二 如图, 中,∠A=3∠B, 求∠C和∠D 的度数
□ABCD
解:∵四边形ABCD是平行四边形
∴∠A = ∠C,∠B= ∠D
AD∥BC
∴∠A +∠B =180°
∵∠A=3∠B
∴∠B=45°∠A=135°
∴∠A = ∠C=135°
∠B= ∠D=45°
练习三:已知 的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
□ABCD
解:在 中,
AB =CD,BC= AD ∵ 的周长为60cm
∴AB+CD+BC+AD=60
即AB+BC=30
又∵AB:BC=3:2
□ABCD
□ABCD
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
练一练
5.5cm
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在 中,如果∠A=42°那么∠B=48° ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠C=145°. ( )
□ABCD
练一练
5.5cm
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在 中,如果∠A=42°那么∠B=48° ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠C=145°. ( )
√
√
×
□ABCD
√
×
×
课堂小结:
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
3. 两平行线的距离相等
