华师版八年级数学下册课件:18.1.2平行四边形的性质(第2课时)(27张PPT)
文档属性
| 名称 | 华师版八年级数学下册课件:18.1.2平行四边形的性质(第2课时)(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:56:52 | ||
图片预览



文档简介
18.1.2平行四边形的性质
1、掌握“平行四边形的对角线互相平分”的性质定理
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
重点:平行四边形的对角线互相平分.
难点:运用“平行四边形的对角线互相平分”这一性质解决简单的问题.
学习目标
八年级 数学
复习
A
D
B
C
定 义
表示方法
性 质
两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。
1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等, 相邻两角互补。
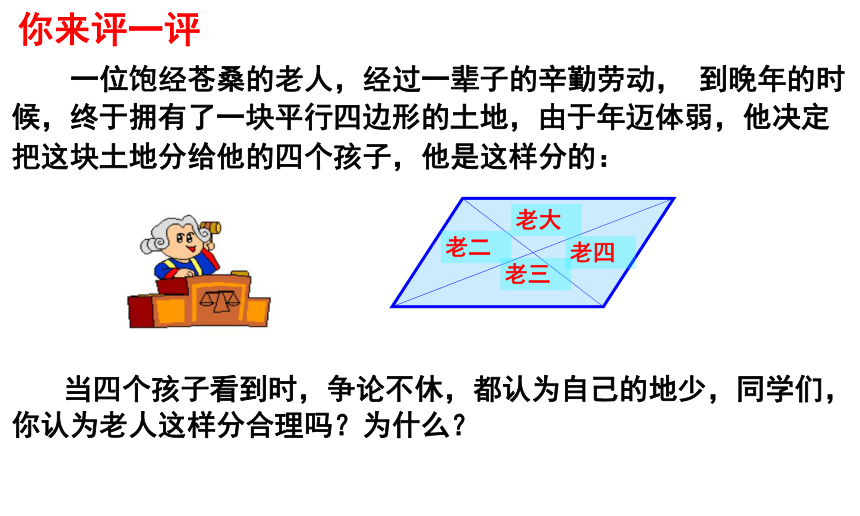
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
你来评一评
知识形成
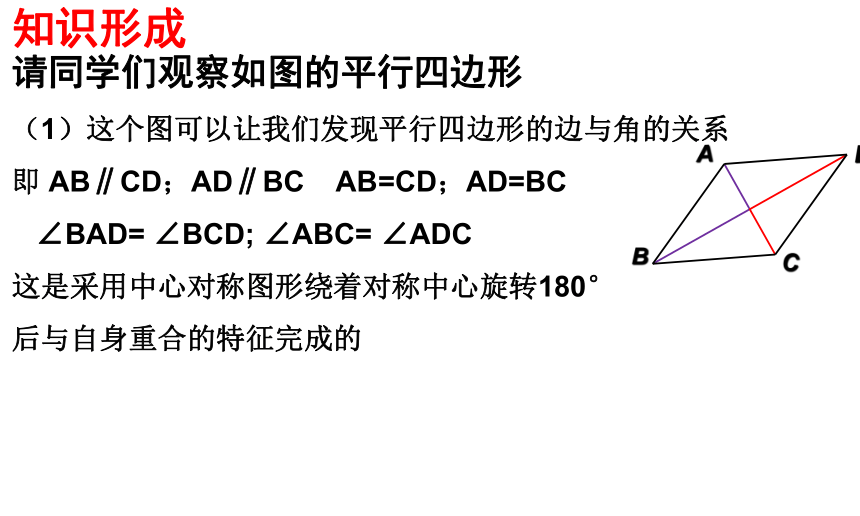
请同学们观察如图的平行四边形
(1)这个图可以让我们发现平行四边形的边与角的关系
即 AB∥CD;AD∥BC AB=CD;AD=BC
∠BAD= ∠BCD; ∠ABC= ∠ADC
这是采用中心对称图形绕着对称中心旋转180°
后与自身重合的特征完成的
A
B
D
C
知识形成
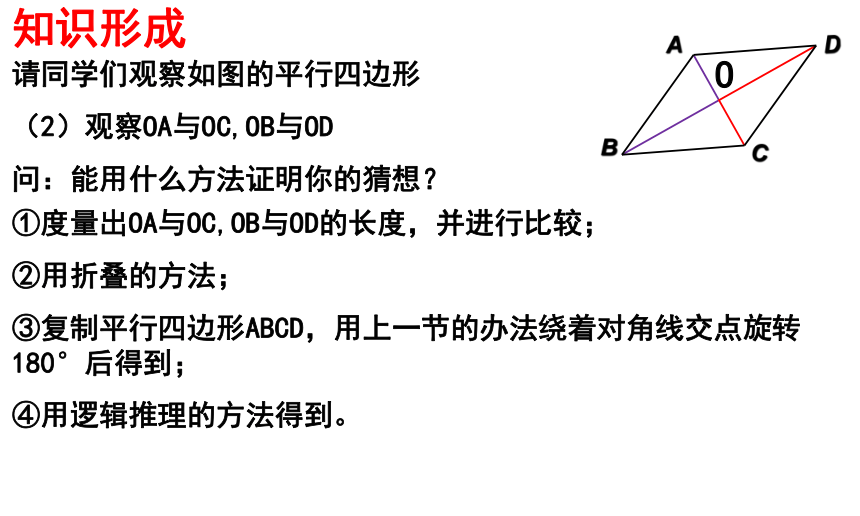
①度量出OA与OC,OB与OD的长度,并进行比较;
②用折叠的方法;
③复制平行四边形ABCD,用上一节的办法绕着对角线交点旋转180°后得到;
④用逻辑推理的方法得到。
A
B
D
C
请同学们观察如图的平行四边形
(2)观察OA与OC,OB与OD
问:能用什么方法证明你的猜想?
O
A
B
D
C
O
A
B
D
C
O
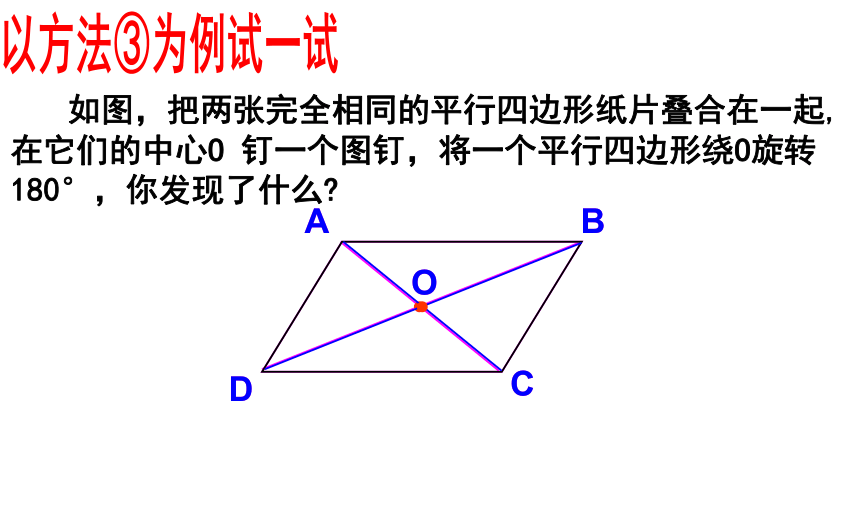
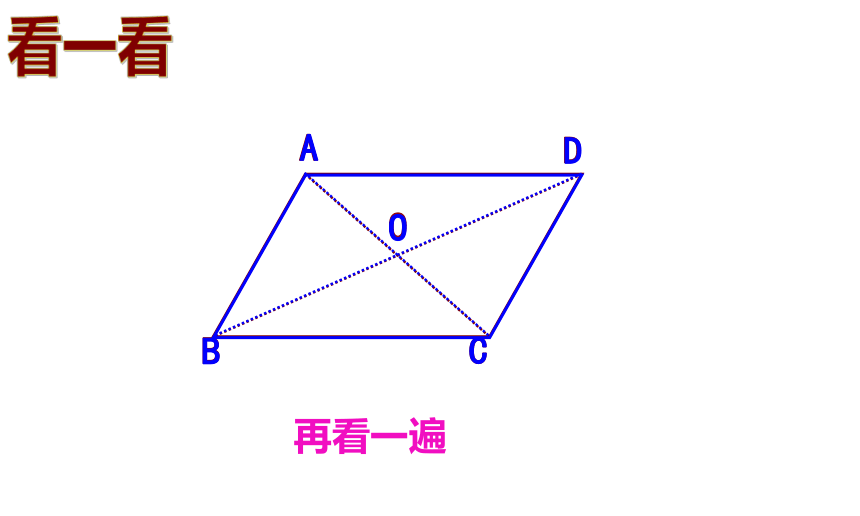
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
*
●
A
D
O
C
B
D
B
O
C
A
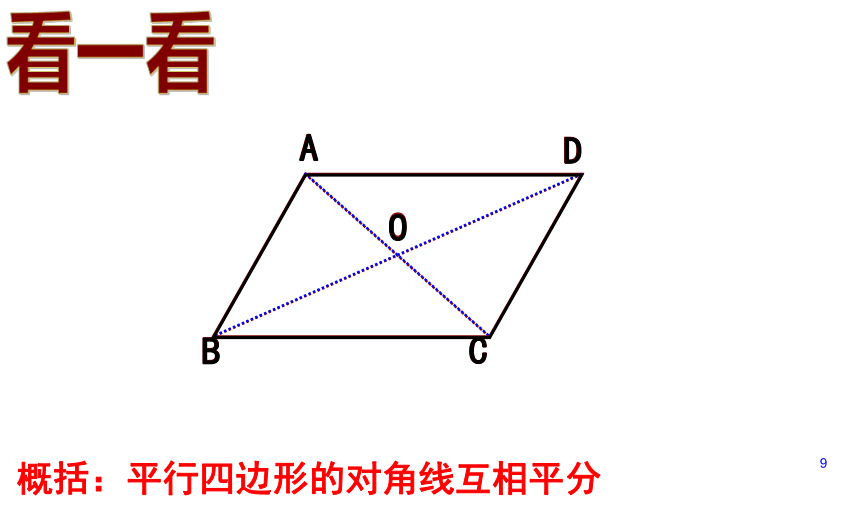
概括:平行四边形的对角线互相平分
*
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
3
2
4
1
证明:平行四边形的对角线互相平分
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
O
A
B
D
C
O
1、如图,在 ABCD中,BC=10cm, AC=8cm, BD=14cm,
(1)△ BOC的周长是多少?说明理由?
(2) △ ABC与△ DBC的周长哪个长,长多少?
10+4+7=21
△ DBC的周长较长
A
B
C
D
O
*
2、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及平行四边形ABCD的面积
A
B
C
D
O
解:∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵AC⊥BC∴△ABC是直角三角形
A
C
D
B
O
●
老大
老四
老三
老二
M
故四人的土地面积相同,老人分地合理。
*
*
1、如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是_________.
O
D
B
A
C
●
1<AD<9
2、平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
3、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
D
O
D
B
A
C
●
4、如图,在平面直角坐标系中, OBCD的顶点O﹑B﹑D的坐标如图所示,则顶点C的 坐标为( )
Y
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
x
O (0,0)
B(5,0)
C
D(2,3)
5、 如图,在 ABCD中, 对角线AC﹑BD相交于点O,AC+BD=20, △AOB的周长等于15,则CD=______
5
O
D
B
A
C
●
O
D
B
A
C
6、如图, ABCD中, 对角线AC﹑BD相交于点O,△AOB的周长等于15,AB=6,则AC、BD和是多少?
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD
∴AC+BD=2AO+2BO=2(AO+BO)
=2×9=18.
O
D
B
A
C
O
D
B
A
C
●
F
E
7:如图, ABCD的对角线AC和BD相较于点O,EF过点O且与边AB、CD分别相交于点E和F.求证:OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
解:∵四边形ABCD是平行四边形,
∴ OB=OD
又∵ AB∥DC,
∴∠EBO=∠FDO.
又∵∠BOE=∠DOF,
∴ △BEO≌△DFO.
∴ OE=OF
O
D
B
A
C
●
F
E
8:如图,在□ ABCD中,对角线AC=21cm,BE ⊥AC ,垂足为点E,且BE=5cm,AD=7cm. 求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则
□ ABCD的面积等于AD·x.
∵ S□ ABCD=2S ΔABC=AC ·BE,
∴ AD·x=AC ·BE,
即7x=21×5,
∴ x=15(cm).
即AD和BC之间的距离为15cm.
你知道其中的理由吗?
D
A
B
C
E
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
1、掌握“平行四边形的对角线互相平分”的性质定理
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
重点:平行四边形的对角线互相平分.
难点:运用“平行四边形的对角线互相平分”这一性质解决简单的问题.
学习目标
八年级 数学
复习
A
D
B
C
定 义
表示方法
性 质
两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。
1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等, 相邻两角互补。
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
你来评一评
知识形成
请同学们观察如图的平行四边形
(1)这个图可以让我们发现平行四边形的边与角的关系
即 AB∥CD;AD∥BC AB=CD;AD=BC
∠BAD= ∠BCD; ∠ABC= ∠ADC
这是采用中心对称图形绕着对称中心旋转180°
后与自身重合的特征完成的
A
B
D
C
知识形成
①度量出OA与OC,OB与OD的长度,并进行比较;
②用折叠的方法;
③复制平行四边形ABCD,用上一节的办法绕着对角线交点旋转180°后得到;
④用逻辑推理的方法得到。
A
B
D
C
请同学们观察如图的平行四边形
(2)观察OA与OC,OB与OD
问:能用什么方法证明你的猜想?
O
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
*
●
A
D
O
C
B
D
B
O
C
A
概括:平行四边形的对角线互相平分
*
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
3
2
4
1
证明:平行四边形的对角线互相平分
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
O
A
B
D
C
O
1、如图,在 ABCD中,BC=10cm, AC=8cm, BD=14cm,
(1)△ BOC的周长是多少?说明理由?
(2) △ ABC与△ DBC的周长哪个长,长多少?
10+4+7=21
△ DBC的周长较长
A
B
C
D
O
*
2、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及平行四边形ABCD的面积
A
B
C
D
O
解:∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵AC⊥BC∴△ABC是直角三角形
A
C
D
B
O
●
老大
老四
老三
老二
M
故四人的土地面积相同,老人分地合理。
*
*
1、如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是_________.
O
D
B
A
C
●
1<AD<9
2、平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
3、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
D
O
D
B
A
C
●
4、如图,在平面直角坐标系中, OBCD的顶点O﹑B﹑D的坐标如图所示,则顶点C的 坐标为( )
Y
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
x
O (0,0)
B(5,0)
C
D(2,3)
5、 如图,在 ABCD中, 对角线AC﹑BD相交于点O,AC+BD=20, △AOB的周长等于15,则CD=______
5
O
D
B
A
C
●
O
D
B
A
C
6、如图, ABCD中, 对角线AC﹑BD相交于点O,△AOB的周长等于15,AB=6,则AC、BD和是多少?
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD
∴AC+BD=2AO+2BO=2(AO+BO)
=2×9=18.
O
D
B
A
C
O
D
B
A
C
●
F
E
7:如图, ABCD的对角线AC和BD相较于点O,EF过点O且与边AB、CD分别相交于点E和F.求证:OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
解:∵四边形ABCD是平行四边形,
∴ OB=OD
又∵ AB∥DC,
∴∠EBO=∠FDO.
又∵∠BOE=∠DOF,
∴ △BEO≌△DFO.
∴ OE=OF
O
D
B
A
C
●
F
E
8:如图,在□ ABCD中,对角线AC=21cm,BE ⊥AC ,垂足为点E,且BE=5cm,AD=7cm. 求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则
□ ABCD的面积等于AD·x.
∵ S□ ABCD=2S ΔABC=AC ·BE,
∴ AD·x=AC ·BE,
即7x=21×5,
∴ x=15(cm).
即AD和BC之间的距离为15cm.
你知道其中的理由吗?
D
A
B
C
E
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
