华师大版八年级下册19.1 矩形的性质 》课件 (共13张PPT)
文档属性
| 名称 | 华师大版八年级下册19.1 矩形的性质 》课件 (共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 17:54:56 | ||
图片预览




文档简介
§19.1 .1矩形的性质
学习目标
1.通过生活实例与活动归纳矩形的定义
与性质
2.理解矩形的性质并会运用矩形的性质
解决相关问题
3、培养学生的观察能力、动手能力、自学能力、计算能力和逻辑思维能力
自学感知:
1、用自制的平行四边形,轻轻的推动其中的一点,你会发现什么?
2、你知道为什么还是平行四边形吗?
3、当改变平行四边形的内角时,使其一个内角恰好为直角,此时平行四边形就变成了一个矩形,你能不能给矩形一个合理的定义?
自学感知:
一般性质:
具备平行四边形所有的性质
对边相等,
对角相等,
对角线互相平分
自学感知:
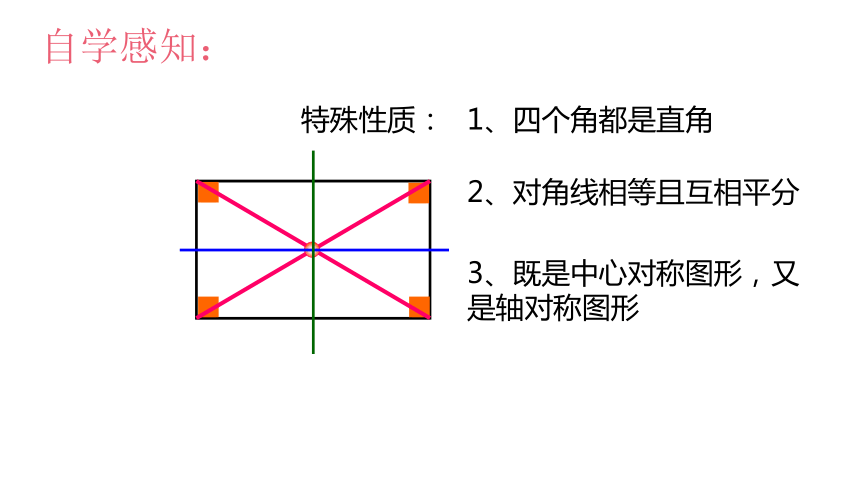
特殊性质:
1、四个角都是直角
2、对角线相等且互相平分
3、既是中心对称图形,又是轴对称图形
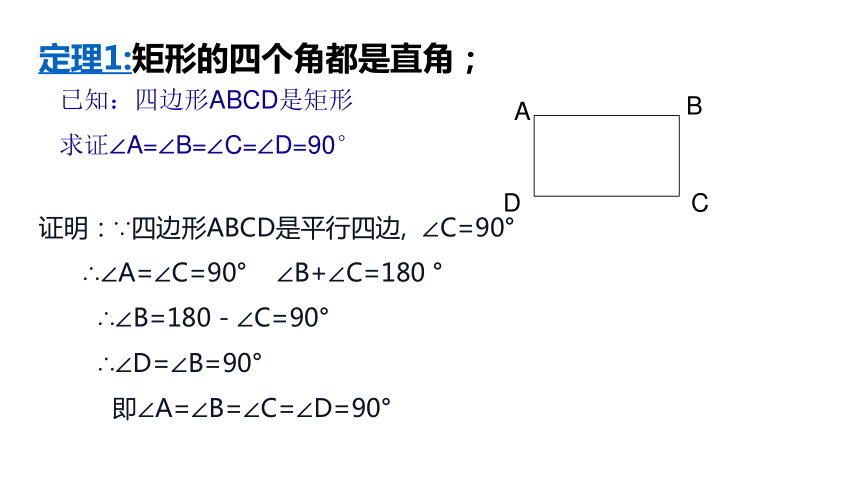
定理1:矩形的四个角都是直角;
证明:∵四边形ABCD是平行四边, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证∠A=∠B=∠C=∠D=90°
A
B
C
D
命题2:矩形的对角线相等;
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
三 矩形的性质
请同学们完成下表
平行四边形
的一边性质
矩形的
性质
对称性
边
角
对角线
中心对称
中心对称
对边相等
对边相等
对角相等
对角相等
四个角都
是直角
对角线互
相平分
对角线相等
例1、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86,对角线的长是13,那么矩形的周长是多少?
A
B
C
D
O
1.矩形具有而平行四边形不具有的性质( )
A. 内角和是360度 B. 对角相等 C. 对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的( )
A. 对角线相等 B. 四个角相等 C. 是轴对称图形 D. 对角线垂直
D
D
学以致用
3、四边形ABCD是矩形
A
B
C
D
O
1)若已知AB=8㎝,AD=6㎝,
则AC= ㎝
OB= ㎝
2)若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
3)若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
10
5
50°
100°
80°
28
48
4.如图,在矩形ABCD中点E在边CD上,将该
矩形沿AE折叠,恰好使点D落在边BC上的
点F处.如果 BAF=60°
求 DAE的大小。
A
B
C
D
F
E
课堂小结:
1、四边形、平行四边形、矩形的关系
两组对边
分别平行
有一个角
是直角
对角线互相平分
对角线
对角线相等
对边平行
边
对边相等
对角相等
角
四个角都是直角
2、矩形的性质
学习目标
1.通过生活实例与活动归纳矩形的定义
与性质
2.理解矩形的性质并会运用矩形的性质
解决相关问题
3、培养学生的观察能力、动手能力、自学能力、计算能力和逻辑思维能力
自学感知:
1、用自制的平行四边形,轻轻的推动其中的一点,你会发现什么?
2、你知道为什么还是平行四边形吗?
3、当改变平行四边形的内角时,使其一个内角恰好为直角,此时平行四边形就变成了一个矩形,你能不能给矩形一个合理的定义?
自学感知:
一般性质:
具备平行四边形所有的性质
对边相等,
对角相等,
对角线互相平分
自学感知:
特殊性质:
1、四个角都是直角
2、对角线相等且互相平分
3、既是中心对称图形,又是轴对称图形
定理1:矩形的四个角都是直角;
证明:∵四边形ABCD是平行四边, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证∠A=∠B=∠C=∠D=90°
A
B
C
D
命题2:矩形的对角线相等;
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
三 矩形的性质
请同学们完成下表
平行四边形
的一边性质
矩形的
性质
对称性
边
角
对角线
中心对称
中心对称
对边相等
对边相等
对角相等
对角相等
四个角都
是直角
对角线互
相平分
对角线相等
例1、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86,对角线的长是13,那么矩形的周长是多少?
A
B
C
D
O
1.矩形具有而平行四边形不具有的性质( )
A. 内角和是360度 B. 对角相等 C. 对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的( )
A. 对角线相等 B. 四个角相等 C. 是轴对称图形 D. 对角线垂直
D
D
学以致用
3、四边形ABCD是矩形
A
B
C
D
O
1)若已知AB=8㎝,AD=6㎝,
则AC= ㎝
OB= ㎝
2)若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
3)若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
10
5
50°
100°
80°
28
48
4.如图,在矩形ABCD中点E在边CD上,将该
矩形沿AE折叠,恰好使点D落在边BC上的
点F处.如果 BAF=60°
求 DAE的大小。
A
B
C
D
F
E
课堂小结:
1、四边形、平行四边形、矩形的关系
两组对边
分别平行
有一个角
是直角
对角线互相平分
对角线
对角线相等
对边平行
边
对边相等
对角相等
角
四个角都是直角
2、矩形的性质
