第二章 相交线与平行线 单元测试 基础卷(含解析)
文档属性
| 名称 | 第二章 相交线与平行线 单元测试 基础卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
相交线与平行线
单元测试基础卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
A.∠B=∠C
B.AD∥BC
C.∠2+∠B=180°
D.AB∥CD
2.在、两座工厂之间要修建一条笔直的公路,从地测得地的走向是南偏东,现、两地要同时开工,若干天后,公路准确对接,则地所修公路的走向应该是(
)
A.北偏西
B.南偏东
C.西偏北
D.北偏西
3.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
4.如图,若AB∥CD,CD∥EF,那么∠BCE=(
)
A.∠1+∠2
B.∠2-∠1
C.180°-∠1+∠2
D.180°-∠2+∠1
5.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
6.下列说法正确的个数有( )
①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④若a∥b,b∥c,则a∥c.
A.1个
B.2个
C.3个
D.4个
7.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC
B.∠AFE=∠ACD
C.∠3=∠4
D.∠1=∠2
8.下面四个图形中,与是对顶角的是(
)
A.
B.
C.
D.
9.下列作图能表示点A到BC的距离的是( )
A.A
B.B
C.C
D.D
10.如图,在中,分别在上,且∥,要使∥,只需再有下列条件中的(
)即可.
A.
B.
C.
D.
二、填空题.(共8小题,每小题3分,满分24分)
11.如图,直线相交于点.重足为,则的度数为__________度
12.如图,AB与BC被AD所截得的内错角是_________;DE与AC被直线AD所截得的内错角是__________;图中∠4的内错角是________.
13.如图,直线l1∥l2且l1,l2被直线l3所截,∠1=∠2=35°,∠P=90°,则∠3=
度.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:_____.
15.如图,已知,,,则__________.
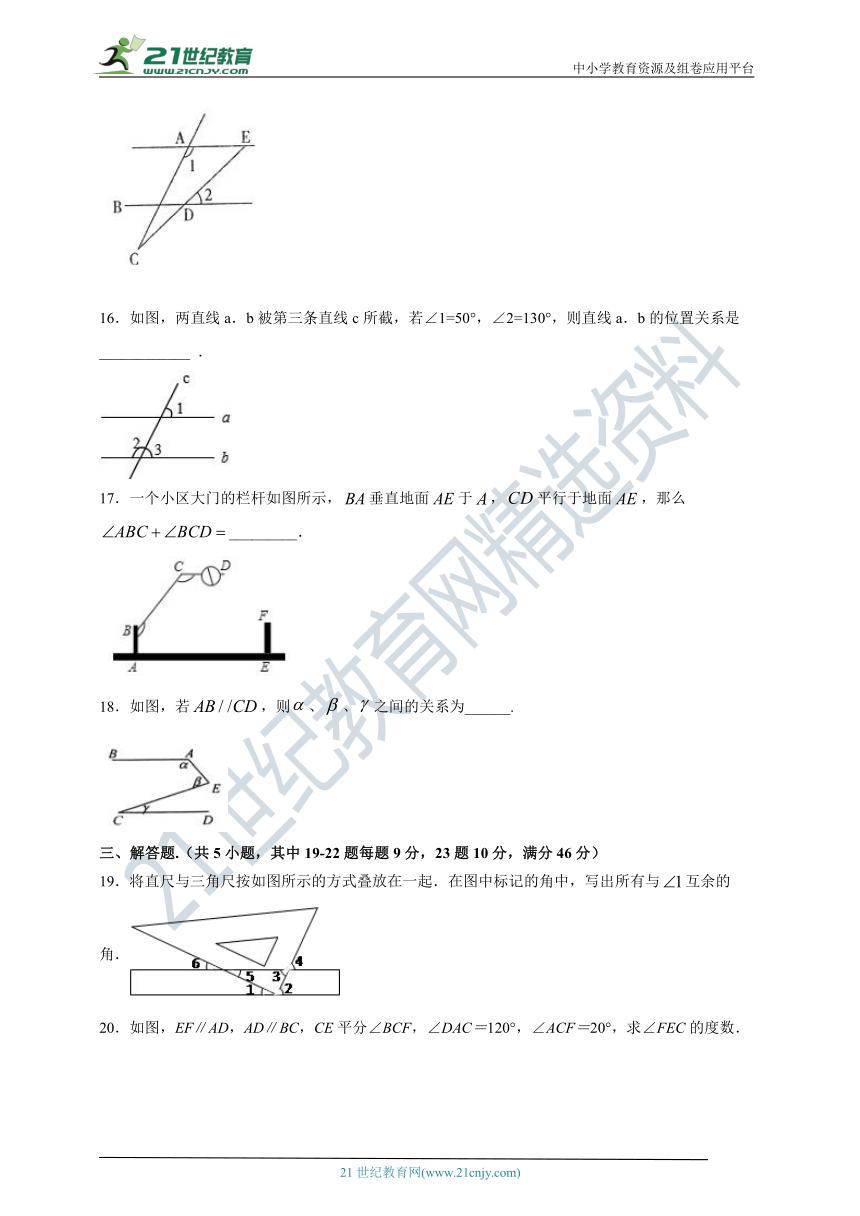
16.如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________
.
17.一个小区大门的栏杆如图所示,垂直地面于,平行于地面,那么_________.
18.如图,若,则、、之间的关系为______.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
19.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与互余的角.
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
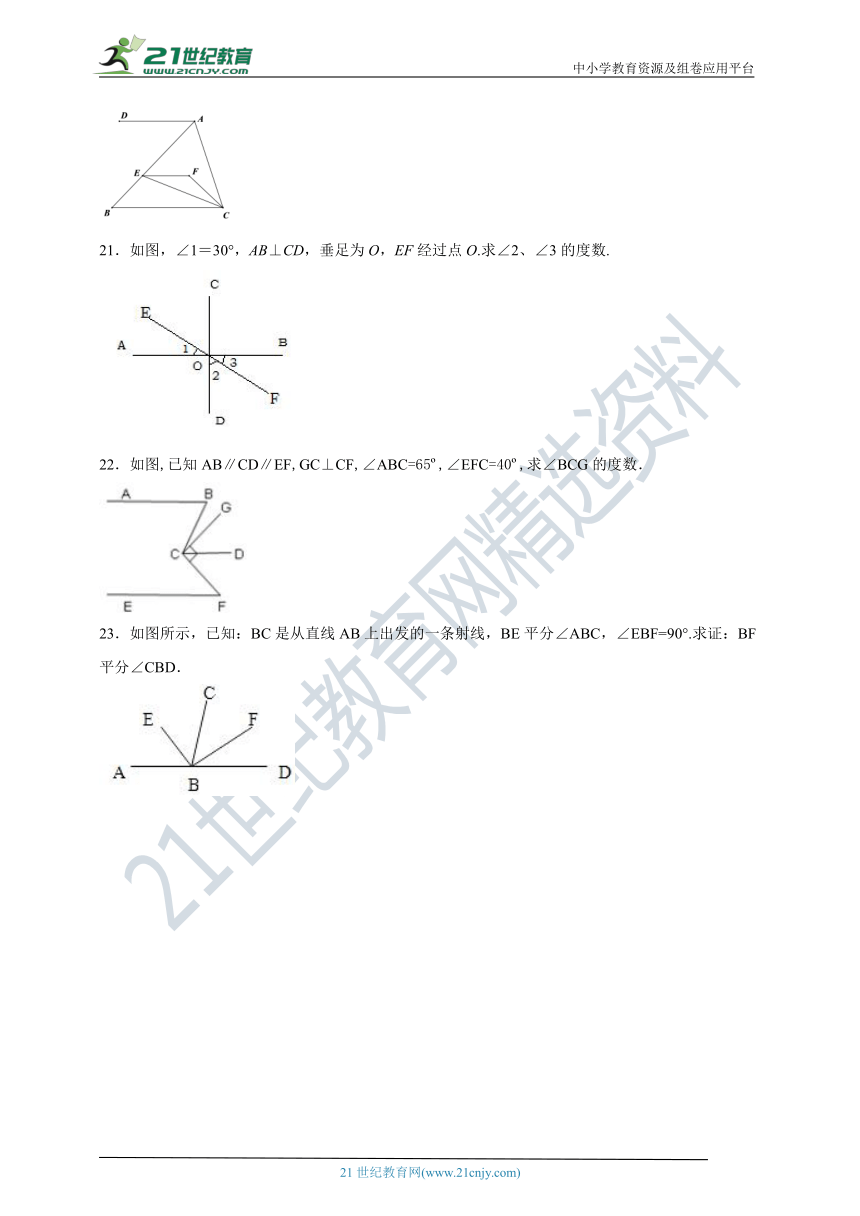
21.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
22.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65?,∠EFC=40?,求∠BCG的度数.
23.如图所示,已知:BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
参考答案
1.A
【详解】
∵∠1=∠B,∠2=∠C,
而∠1+∠2=180°,
∴∠B+∠C=180°,所以A选项错误;
∵∠1=∠B,
∴AD∥BC,所以B选项正确;
∴∠2+∠B=180°,所以C选项正确;
∵∠B+∠C=180°,
∴AB∥DC,所以D选项正确;
故选A.
2.A
【解析】
如图,连接AB,
由题意得:∠CAB=52°,
∵DB∥AC,
∴∠CAB=∠ABD=52°,
∴B地所修公路走向应该是北偏西52°.
故选A.
3.B
【解析】
试题解析:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角
则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选B.
4.D
【详解】
解:∵AB∥CD,
∴∠BCD=∠1,
∵CD∥EF,
∴∠DCE=180°-∠2,
∴∠BCE=∠BCD+∠DCE=180°-∠2+∠1.
故选D.
5.D
【详解】
解:A选项:只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B选项:在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C选项:相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D选项:由平行公理的推论知,故D选项正确.
故选D.
6.A
【详解】
解:①如图,直线AB、CD被直线GH所截,∠AGH与∠CHF是同位角,但它们不相等,故说法错误;
②同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
③应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
④平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是④共1个.
故选A.
7.C
【详解】
解:∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行,A选项错误;
∠AFE=∠ACD,∠1=∠2是EF和BC被AC和EC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC,B选项和D选项错误;
∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC,C选项正确.
故选:C.
8.D
【详解】
解:由对顶角的定义,得D选项是对顶角,
故选:D.
9.B
【详解】
解:A.BD表示点B到AC的距离,故A选项错误;
B.
AD表示点A到BC的距离,故B选项正确;?
C.
AD表示点D到AB的距离,故C选项错误;?
D.
CD表示点C到AB的距离,故D选项错误;?
故选B.
10.B
【解析】
∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,
∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).
所以只需满足下列条件中的∠1=∠DFE.故选B.
11.
【详解】
∵
∴∠EOB=90°
∵∠EOC=35°
∴∠BOC=∠EOB+∠EOC=125°
∴∠AOD=∠BOC
=125°
故答案为:125
12.∠1和∠3
∠2和∠4
∠5和∠2
【详解】
结合图形可得AB与BC被AD所截得的内错角是∠1和∠3;
DE与AC被直线AD所截得的内错角是∠2和∠4;
因为∠4和∠5是直线AB和AD被直线ED所截构成的内错角,∠4和∠2是直线DE和AC被直线AD所截构成的内错角,
所以图中∠4的内错角是∠5和∠2.
13.55.
【详解】
∵直线l1∥l2被直线l3所截,
∴∠CAB=180°?∠1?∠2=180°?35°?35°=110°,
∵△ABP中,∠2=35°,∠P=90°,
∴∠PAB=90°?35°=55°,
∴∠3=∠CAB?∠PAB=110°?55°=55°,.
故答案为55.
14.垂线段最短
【解析】
根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
15.20°
【详解】
∵,,
∴∠AEC=,
∵∠1+∠AEC+∠C=180°,
∴∠C=180°-130°-30°=20°.
故答案是:20°.
16.平行
【解析】
详解:∵∠2+∠3=180°,∠2=130°,
∴∠3=50°,
∵∠1=50°,
∴∠1=∠3,
∴a∥b.
故答案为平行.
17.
【详解】
解:作CH⊥AE于H,如图,
∵AB⊥AE,CH⊥AE,
∴AB∥CH,
∴∠ABC+∠BCH=180°,
∵CD∥AE,
∴∠DCH+∠CHE=180°,
而∠CHE=90°,
∴∠DCH=90°,
∴∠ABC+∠BCD=180°+90°=270°.
故答案为270°.
18.
【详解】
过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β?∠γ=180°.
故答案为∠α+∠β?∠γ=180°.
19..
【解析】
解答:
∵直尺的两边平行,
∴∠2=∠3;
∵∠3=∠4,∠1+∠2=90°,
∴∠1的余角有:∠2,∠3,∠4.
20.20°
【详解】
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB?∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
21.∠2=60°,∠3=30°
【详解】
解:∵直线AB和EF交于点O,∠1=30°,
∴∠3=∠1=30°,
∵AB⊥CD,
∴∠BOD=90°,
∴∠2=90°﹣30°=60°.
22.15?;
【解析】
根据AB∥CD∥EF,可得∠BCD、∠DCF的度数,又GC⊥CF,可得∠GCD,从而得到∠BCG的度数.
AB∥CD∥EF,
∠BCD=∠BCD—∠B=65?,∠DCF=∠F=40?,
GC⊥CF,
∠GCF=90?,
∠GCD=90?—40?=50?,
∠BCG=∠BCD—∠GCD=65?—50?=15?.
23.见解析
【解析】
试题分析:由BE平分∠ABC,可得∠CBE=∠ABC,则∠CBF=90°-∠ABC,从而可得∠DBF=180°-∠ABC-∠CBF=180°-∠ABC-(90°-∠ABC)=
90°-∠ABC=∠CBF,即可证得结论.
∵BE平分∠ABC,
∴∠CBE=∠ABC,
∵∠EBF=90°,
∴∠CBF=90°-∠ABC,
∴∠DBF=180°-∠ABC-∠CBF=180°-∠ABC-(90°-∠ABC)=
90°-∠ABC=∠CBF.
∴BF平分∠CBD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
相交线与平行线
单元测试基础卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
A.∠B=∠C
B.AD∥BC
C.∠2+∠B=180°
D.AB∥CD
2.在、两座工厂之间要修建一条笔直的公路,从地测得地的走向是南偏东,现、两地要同时开工,若干天后,公路准确对接,则地所修公路的走向应该是(
)
A.北偏西
B.南偏东
C.西偏北
D.北偏西
3.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
4.如图,若AB∥CD,CD∥EF,那么∠BCE=(
)
A.∠1+∠2
B.∠2-∠1
C.180°-∠1+∠2
D.180°-∠2+∠1
5.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
6.下列说法正确的个数有( )
①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④若a∥b,b∥c,则a∥c.
A.1个
B.2个
C.3个
D.4个
7.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC
B.∠AFE=∠ACD
C.∠3=∠4
D.∠1=∠2
8.下面四个图形中,与是对顶角的是(
)
A.
B.
C.
D.
9.下列作图能表示点A到BC的距离的是( )
A.A
B.B
C.C
D.D
10.如图,在中,分别在上,且∥,要使∥,只需再有下列条件中的(
)即可.
A.
B.
C.
D.
二、填空题.(共8小题,每小题3分,满分24分)
11.如图,直线相交于点.重足为,则的度数为__________度
12.如图,AB与BC被AD所截得的内错角是_________;DE与AC被直线AD所截得的内错角是__________;图中∠4的内错角是________.
13.如图,直线l1∥l2且l1,l2被直线l3所截,∠1=∠2=35°,∠P=90°,则∠3=
度.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:_____.
15.如图,已知,,,则__________.
16.如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________
.
17.一个小区大门的栏杆如图所示,垂直地面于,平行于地面,那么_________.
18.如图,若,则、、之间的关系为______.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
19.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与互余的角.
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
21.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
22.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65?,∠EFC=40?,求∠BCG的度数.
23.如图所示,已知:BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
参考答案
1.A
【详解】
∵∠1=∠B,∠2=∠C,
而∠1+∠2=180°,
∴∠B+∠C=180°,所以A选项错误;
∵∠1=∠B,
∴AD∥BC,所以B选项正确;
∴∠2+∠B=180°,所以C选项正确;
∵∠B+∠C=180°,
∴AB∥DC,所以D选项正确;
故选A.
2.A
【解析】
如图,连接AB,
由题意得:∠CAB=52°,
∵DB∥AC,
∴∠CAB=∠ABD=52°,
∴B地所修公路走向应该是北偏西52°.
故选A.
3.B
【解析】
试题解析:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角
则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选B.
4.D
【详解】
解:∵AB∥CD,
∴∠BCD=∠1,
∵CD∥EF,
∴∠DCE=180°-∠2,
∴∠BCE=∠BCD+∠DCE=180°-∠2+∠1.
故选D.
5.D
【详解】
解:A选项:只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B选项:在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C选项:相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D选项:由平行公理的推论知,故D选项正确.
故选D.
6.A
【详解】
解:①如图,直线AB、CD被直线GH所截,∠AGH与∠CHF是同位角,但它们不相等,故说法错误;
②同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
③应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
④平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是④共1个.
故选A.
7.C
【详解】
解:∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行,A选项错误;
∠AFE=∠ACD,∠1=∠2是EF和BC被AC和EC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC,B选项和D选项错误;
∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC,C选项正确.
故选:C.
8.D
【详解】
解:由对顶角的定义,得D选项是对顶角,
故选:D.
9.B
【详解】
解:A.BD表示点B到AC的距离,故A选项错误;
B.
AD表示点A到BC的距离,故B选项正确;?
C.
AD表示点D到AB的距离,故C选项错误;?
D.
CD表示点C到AB的距离,故D选项错误;?
故选B.
10.B
【解析】
∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,
∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).
所以只需满足下列条件中的∠1=∠DFE.故选B.
11.
【详解】
∵
∴∠EOB=90°
∵∠EOC=35°
∴∠BOC=∠EOB+∠EOC=125°
∴∠AOD=∠BOC
=125°
故答案为:125
12.∠1和∠3
∠2和∠4
∠5和∠2
【详解】
结合图形可得AB与BC被AD所截得的内错角是∠1和∠3;
DE与AC被直线AD所截得的内错角是∠2和∠4;
因为∠4和∠5是直线AB和AD被直线ED所截构成的内错角,∠4和∠2是直线DE和AC被直线AD所截构成的内错角,
所以图中∠4的内错角是∠5和∠2.
13.55.
【详解】
∵直线l1∥l2被直线l3所截,
∴∠CAB=180°?∠1?∠2=180°?35°?35°=110°,
∵△ABP中,∠2=35°,∠P=90°,
∴∠PAB=90°?35°=55°,
∴∠3=∠CAB?∠PAB=110°?55°=55°,.
故答案为55.
14.垂线段最短
【解析】
根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
15.20°
【详解】
∵,,
∴∠AEC=,
∵∠1+∠AEC+∠C=180°,
∴∠C=180°-130°-30°=20°.
故答案是:20°.
16.平行
【解析】
详解:∵∠2+∠3=180°,∠2=130°,
∴∠3=50°,
∵∠1=50°,
∴∠1=∠3,
∴a∥b.
故答案为平行.
17.
【详解】
解:作CH⊥AE于H,如图,
∵AB⊥AE,CH⊥AE,
∴AB∥CH,
∴∠ABC+∠BCH=180°,
∵CD∥AE,
∴∠DCH+∠CHE=180°,
而∠CHE=90°,
∴∠DCH=90°,
∴∠ABC+∠BCD=180°+90°=270°.
故答案为270°.
18.
【详解】
过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β?∠γ=180°.
故答案为∠α+∠β?∠γ=180°.
19..
【解析】
解答:
∵直尺的两边平行,
∴∠2=∠3;
∵∠3=∠4,∠1+∠2=90°,
∴∠1的余角有:∠2,∠3,∠4.
20.20°
【详解】
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB?∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
21.∠2=60°,∠3=30°
【详解】
解:∵直线AB和EF交于点O,∠1=30°,
∴∠3=∠1=30°,
∵AB⊥CD,
∴∠BOD=90°,
∴∠2=90°﹣30°=60°.
22.15?;
【解析】
根据AB∥CD∥EF,可得∠BCD、∠DCF的度数,又GC⊥CF,可得∠GCD,从而得到∠BCG的度数.
AB∥CD∥EF,
∠BCD=∠BCD—∠B=65?,∠DCF=∠F=40?,
GC⊥CF,
∠GCF=90?,
∠GCD=90?—40?=50?,
∠BCG=∠BCD—∠GCD=65?—50?=15?.
23.见解析
【解析】
试题分析:由BE平分∠ABC,可得∠CBE=∠ABC,则∠CBF=90°-∠ABC,从而可得∠DBF=180°-∠ABC-∠CBF=180°-∠ABC-(90°-∠ABC)=
90°-∠ABC=∠CBF,即可证得结论.
∵BE平分∠ABC,
∴∠CBE=∠ABC,
∵∠EBF=90°,
∴∠CBF=90°-∠ABC,
∴∠DBF=180°-∠ABC-∠CBF=180°-∠ABC-(90°-∠ABC)=
90°-∠ABC=∠CBF.
∴BF平分∠CBD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
