第二章 相交线与平行线 单元测试 培优卷(含解析)
文档属性
| 名称 | 第二章 相交线与平行线 单元测试 培优卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 14:19:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
相交线与平行线
单元测试培优卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,下列各式中正确的是(
)
A.
B.
C.
D.
2.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠5=∠B
D.∠B
+∠BDC=180°
3.如图,已知∠B+∠DAB=180°,AC平分∠DAB,如果∠C=50°,那么∠B等于( )
A.50°
B.60°
C.70°
D.80°
4.如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A.∠1+∠2﹣∠3
B.∠1+∠3﹣∠2
C.180°+∠3﹣∠1﹣∠2
D.∠2+∠3﹣∠1﹣180°
5.对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.∠1=∠2
B.∠2=∠4
C.∠3=∠4
D.∠1+∠4=180°
6.如图.已知.直线分别交于点平分.若.则的度数为(
)
A.
B.
C.
D.
7.如图,若AB∥CD,则α、β、γ之间的关系为( )
A.α+β+γ=360°
B.α﹣β+γ=180°
C.α+β﹣γ=180°
D.α+β+γ=180°
8.把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有(
)
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.
A.1个
B.2个
C.3个
D.4个
9.如图所示,下列推理正确的是
( )
A.因为∠1=∠4,所以BC∥AD
B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180°
D.因为∠1+∠2+∠C=180°,所以BC∥AD
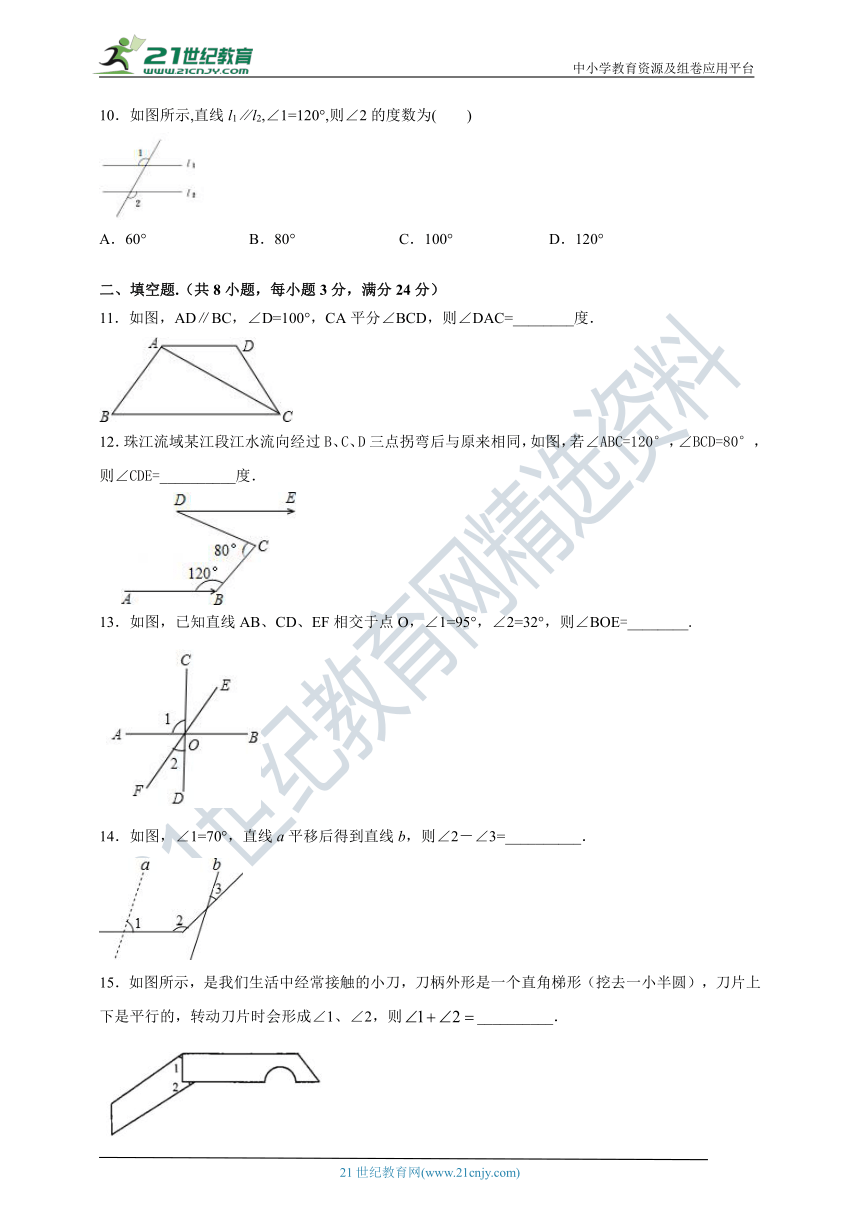
10.如图所示,直线l1∥l2,∠1=120°,则∠2的度数为( )
A.60°
B.80°
C.100°
D.120°
二、填空题.(共8小题,每小题3分,满分24分)
11.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC=________度.
12.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.
13.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
14.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=__________.
15.如图所示,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(挖去一小半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则__________.
16.已知OA⊥OC于O,∠AOB∶∠AOC=2∶3,则∠BOC的度数为____________度.
17.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是________
18.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为_____.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
19.如图,已知射线与直线交于点,平分,于,,且.
(1)求的度数;
(2)试说明平分.
20.如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示的方式折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;
(2)如果∠C=130°,求∠AEB的度数.
21.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
22.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
.
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
23.如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
参考答案
1.D
【解析】
试题分析:延长TS,
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠ESR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
故选D.
2.A
【详解】
解:选项A中,∠1=∠2,只可以判定AC//BD(内错角相等,两直线平行),所以A错误;
选项B中,∠3=∠4,可以判定AB//CD(内错角相等,两直线平行),所以正确;
选项C中,∠5=∠B,AB//CD(内错角相等,两直线平行),所以正确;
选项D中,∠B
+∠BDC=180°,可以判定AB//CD(同旁内角互补,两直线平行),所以正确;
故答案为A.
3.D
【解析】
∵∠B+∠DAB=180°,
∴AD//BC,
∴∠DAC=∠C,
又∵∠C=50°,
∴∠DAC=50°,
又∵AC平分∠DAB,
∴∠DAB=2∠DAC=100°,
又∵∠B+∠DAB=180°,
∴∠B=180°-100°=80°.
故选D.
4.D
【解析】
试题解析:过点E作EG∥AB,过点F作FH∥CD,
∵AB∥CD,
∴AB∥CD∥EG∥FH,
∴∠1=∠AEG,
∴∠GEF=∠2-∠1,
∵EG∥FH,
∴∠EFH=180°-∠GEF=180°-(∠2-∠1)=180°-∠2+∠1,
∴∠CFH=∠3-∠EFH=∠3-(180°-∠2+∠1)=∠3+∠2-∠2-180°,
∵FH∥CD,
∴∠4=∠3+∠2-∠1-180°,
故选D.
5.D
【详解】
A.
∠1=∠2,不能得到a∥b,故错误;
B.
∠2=∠4,不是同位角相等,故错误;
C.
∠3=∠4,不是同位角相等,故错误;
D.
∠1+∠4=180°,先利用对顶角相等,再推出同旁内角互补来得到a∥b.
6.B
【详解】
解:∵AB∥CD,
∴∠1+∠BEF=180°,∠2=∠BEG,
∴∠BEF=180°-50°=130°,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=65°.
故选:B.
7.C
【详解】
解:过点E作EF∥AB,如图,∵AB∥CD,AB∥EF,∴CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴∠FEA=β﹣γ,∴α+(β﹣γ)=180°,即α+β﹣γ=180°.
故选:C.
8.D
【详解】
解:(1)∵AE∥BG,∠EFB=32°,
∴∠C′EF=∠EFB=32°,故本小题正确;
(2)∵AE∥BG,∠EFB=32°,
∴∠GEF=∠C′EF=32°,
∴∠AEC=180°-32°-32°=116°,故本小题正确;
(3)∵∠C′EF=32°,
∴∠GEF=∠C′EF=32°,
∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°,
∵AC′∥BD′,
∴∠BGE=∠C′EG=64°,故本小题正确;
(4)∵∠BGE=64°,
∴∠CGF=∠BGE=64°,
∵DF∥CG,
∴∠BFD=180°-∠CGF=180°-64°=116°,故本小题正确.
故选D.
9.C
【解析】
【详解】
A、∵∠1=∠4,
∴AB∥CD,故本选项错误;
B、∵∠2=∠3,
∴BC∥AD,故本选项错误;
C、∵AD∥BC,
∴∠BCD+∠ADC=180°,故本选项正确;
D、∵∠1+∠2+∠C=180°,
∴AB∥CD,故本选项错误;
故选C.
10.D
【详解】
∵直线l1∥l2,,∠1=120°,
∴∠1的同位角是120°,
∴∠2=∠1的同位角=120°.
故选D.
11.40°
【详解】
∵AD∥BC,
∴∠BCD=180°-∠D=80°,
又∵CA平分∠BCD,
∴∠ACB=∠BCD=40°,
∴∠DAC=∠ACB=40°.
12.20
【详解】
解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为20.
13.53°
【解析】
由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数.
14.110°
【详解】
解:如图:延长直线:
∵a平移后得到直线b,
∴a∥b,
∴∠5=180°-∠1=180°-70°=110°,
又∵∠2=∠4+∠5,∠3=∠4,
∴∠2-∠3=∠5=110°
故答案为:110°.
15.
【详解】
解:如图,过点O作OP∥AB,则∠1=∠AOP.
∵AB∥CD,
∴OP∥CD,
∴∠2=∠POC,
∵刀柄外形是一个直角梯形,
∴∠AOP+∠POC=90°,
∴∠1+∠2=90°.
16.30°或150°
【详解】
∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=3:2,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.如图,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故答案为30°或150°.
17.150°
【解析】
如图,过点B作BG∥AE,
因为AE∥CD,所以AE∥BG∥CD.
所以∠A=∠2,∠1+∠C=180°.
因为∠A=120°,所以∠2=120°,所以∠1=150°-120°=30°.
所以∠C=180°-30°=150°,故答案为150°.
18.200m
【详解】
解:∵荷塘中小桥的总长为100米,
∴荷塘周长为:2×100=200(m).
故答案为:200m.
19.(1);(2)证明见解析
【详解】
(1)解:∵
∴
∵
∴,
∵平分,
∴
∴;
(2)证明:∵
∴
∴
∵,
又∵
∴,
,
平分.
20.(1)E//DC;(2)∠AEB=65°
【详解】
(1)E∥DC
由折叠可知∠AE=∠B=90°
∵∠D=90°
∴∠AE=∠D
∴E∥DC
(2)∵B′E∥DC
∴∠EB=∠C=130°
由折叠可知∠AEB=∠AE,
∴∠AEB=∠EB=×130°=65°
故答案为:65°
21.32.5°.
【解析】
试题解析:
∵
AB∥CD,∴
∠B+∠BCE
=180°(两直线平行,同旁内角互补)
∵
∠B
=65°,∴
∠BCE
=115°
∵
CM平分∠BCE,∴
∠ECM=∠BCE
=57.5°
∵
∠ECM
+∠MCN
+∠NCD
=180°,∠MCN
=90°
∴
∠NCD
=180°-∠ECM-∠MCN
=180°-57.5°-90°=32.5°.
22.(1)AB∥CD,理由见解析;(2)∠BAE+∠MCD=90°;(3)∠BAC=∠PQC+∠QPC,理由见解析
【详解】
(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+∠MCD=90°;
过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+∠MCD=90°;
(3)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
23.(1)与∠D相等的角为∠DCG,∠ECF,∠B(2)155°(3)25°或155°
【详解】
解:(1)与∠D相等的角为∠DCG,∠ECF,∠B.(1分)理由如下:
∵AD∥BC,
∴∠D=∠DCG.
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG=∠D.
∵AB∥DC,
∴∠B=∠DCG=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B.
(2)∵∠ECF=25°,∠DCE=90°,
∴∠FCD=65°.
又∵∠BCF=90°,
∴∠BCD=65°+90°=155°.
(3)分两种情况进行讨论:
①如图a,当点C在线段BH上时,点F在DA的延长线上,此时∠ECF=∠DCG=∠B=25°.
∵AD∥BC,
∴∠BAF=∠B=25°;
②如图b,当点C在BH的延长线上时,点F在线段AD上.
∵∠B=25°,AD∥BC,
∴∠BAF=180°-25°=155°.
综上所述,∠BAF的度数为25°或155°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
相交线与平行线
单元测试培优卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题.(共10小题,每小题3分,满分30分)
1.如图,下列各式中正确的是(
)
A.
B.
C.
D.
2.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠5=∠B
D.∠B
+∠BDC=180°
3.如图,已知∠B+∠DAB=180°,AC平分∠DAB,如果∠C=50°,那么∠B等于( )
A.50°
B.60°
C.70°
D.80°
4.如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A.∠1+∠2﹣∠3
B.∠1+∠3﹣∠2
C.180°+∠3﹣∠1﹣∠2
D.∠2+∠3﹣∠1﹣180°
5.对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.∠1=∠2
B.∠2=∠4
C.∠3=∠4
D.∠1+∠4=180°
6.如图.已知.直线分别交于点平分.若.则的度数为(
)
A.
B.
C.
D.
7.如图,若AB∥CD,则α、β、γ之间的关系为( )
A.α+β+γ=360°
B.α﹣β+γ=180°
C.α+β﹣γ=180°
D.α+β+γ=180°
8.把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有(
)
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.
A.1个
B.2个
C.3个
D.4个
9.如图所示,下列推理正确的是
( )
A.因为∠1=∠4,所以BC∥AD
B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180°
D.因为∠1+∠2+∠C=180°,所以BC∥AD
10.如图所示,直线l1∥l2,∠1=120°,则∠2的度数为( )
A.60°
B.80°
C.100°
D.120°
二、填空题.(共8小题,每小题3分,满分24分)
11.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC=________度.
12.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.
13.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
14.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=__________.
15.如图所示,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(挖去一小半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则__________.
16.已知OA⊥OC于O,∠AOB∶∠AOC=2∶3,则∠BOC的度数为____________度.
17.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是________
18.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为_____.
三、解答题.(共5小题,其中19-22题每题9分,23题10分,满分46分)
19.如图,已知射线与直线交于点,平分,于,,且.
(1)求的度数;
(2)试说明平分.
20.如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示的方式折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;
(2)如果∠C=130°,求∠AEB的度数.
21.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
22.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
.
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
23.如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
参考答案
1.D
【解析】
试题分析:延长TS,
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠ESR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
故选D.
2.A
【详解】
解:选项A中,∠1=∠2,只可以判定AC//BD(内错角相等,两直线平行),所以A错误;
选项B中,∠3=∠4,可以判定AB//CD(内错角相等,两直线平行),所以正确;
选项C中,∠5=∠B,AB//CD(内错角相等,两直线平行),所以正确;
选项D中,∠B
+∠BDC=180°,可以判定AB//CD(同旁内角互补,两直线平行),所以正确;
故答案为A.
3.D
【解析】
∵∠B+∠DAB=180°,
∴AD//BC,
∴∠DAC=∠C,
又∵∠C=50°,
∴∠DAC=50°,
又∵AC平分∠DAB,
∴∠DAB=2∠DAC=100°,
又∵∠B+∠DAB=180°,
∴∠B=180°-100°=80°.
故选D.
4.D
【解析】
试题解析:过点E作EG∥AB,过点F作FH∥CD,
∵AB∥CD,
∴AB∥CD∥EG∥FH,
∴∠1=∠AEG,
∴∠GEF=∠2-∠1,
∵EG∥FH,
∴∠EFH=180°-∠GEF=180°-(∠2-∠1)=180°-∠2+∠1,
∴∠CFH=∠3-∠EFH=∠3-(180°-∠2+∠1)=∠3+∠2-∠2-180°,
∵FH∥CD,
∴∠4=∠3+∠2-∠1-180°,
故选D.
5.D
【详解】
A.
∠1=∠2,不能得到a∥b,故错误;
B.
∠2=∠4,不是同位角相等,故错误;
C.
∠3=∠4,不是同位角相等,故错误;
D.
∠1+∠4=180°,先利用对顶角相等,再推出同旁内角互补来得到a∥b.
6.B
【详解】
解:∵AB∥CD,
∴∠1+∠BEF=180°,∠2=∠BEG,
∴∠BEF=180°-50°=130°,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=65°.
故选:B.
7.C
【详解】
解:过点E作EF∥AB,如图,∵AB∥CD,AB∥EF,∴CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴∠FEA=β﹣γ,∴α+(β﹣γ)=180°,即α+β﹣γ=180°.
故选:C.
8.D
【详解】
解:(1)∵AE∥BG,∠EFB=32°,
∴∠C′EF=∠EFB=32°,故本小题正确;
(2)∵AE∥BG,∠EFB=32°,
∴∠GEF=∠C′EF=32°,
∴∠AEC=180°-32°-32°=116°,故本小题正确;
(3)∵∠C′EF=32°,
∴∠GEF=∠C′EF=32°,
∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°,
∵AC′∥BD′,
∴∠BGE=∠C′EG=64°,故本小题正确;
(4)∵∠BGE=64°,
∴∠CGF=∠BGE=64°,
∵DF∥CG,
∴∠BFD=180°-∠CGF=180°-64°=116°,故本小题正确.
故选D.
9.C
【解析】
【详解】
A、∵∠1=∠4,
∴AB∥CD,故本选项错误;
B、∵∠2=∠3,
∴BC∥AD,故本选项错误;
C、∵AD∥BC,
∴∠BCD+∠ADC=180°,故本选项正确;
D、∵∠1+∠2+∠C=180°,
∴AB∥CD,故本选项错误;
故选C.
10.D
【详解】
∵直线l1∥l2,,∠1=120°,
∴∠1的同位角是120°,
∴∠2=∠1的同位角=120°.
故选D.
11.40°
【详解】
∵AD∥BC,
∴∠BCD=180°-∠D=80°,
又∵CA平分∠BCD,
∴∠ACB=∠BCD=40°,
∴∠DAC=∠ACB=40°.
12.20
【详解】
解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为20.
13.53°
【解析】
由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数.
14.110°
【详解】
解:如图:延长直线:
∵a平移后得到直线b,
∴a∥b,
∴∠5=180°-∠1=180°-70°=110°,
又∵∠2=∠4+∠5,∠3=∠4,
∴∠2-∠3=∠5=110°
故答案为:110°.
15.
【详解】
解:如图,过点O作OP∥AB,则∠1=∠AOP.
∵AB∥CD,
∴OP∥CD,
∴∠2=∠POC,
∵刀柄外形是一个直角梯形,
∴∠AOP+∠POC=90°,
∴∠1+∠2=90°.
16.30°或150°
【详解】
∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=3:2,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.如图,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故答案为30°或150°.
17.150°
【解析】
如图,过点B作BG∥AE,
因为AE∥CD,所以AE∥BG∥CD.
所以∠A=∠2,∠1+∠C=180°.
因为∠A=120°,所以∠2=120°,所以∠1=150°-120°=30°.
所以∠C=180°-30°=150°,故答案为150°.
18.200m
【详解】
解:∵荷塘中小桥的总长为100米,
∴荷塘周长为:2×100=200(m).
故答案为:200m.
19.(1);(2)证明见解析
【详解】
(1)解:∵
∴
∵
∴,
∵平分,
∴
∴;
(2)证明:∵
∴
∴
∵,
又∵
∴,
,
平分.
20.(1)E//DC;(2)∠AEB=65°
【详解】
(1)E∥DC
由折叠可知∠AE=∠B=90°
∵∠D=90°
∴∠AE=∠D
∴E∥DC
(2)∵B′E∥DC
∴∠EB=∠C=130°
由折叠可知∠AEB=∠AE,
∴∠AEB=∠EB=×130°=65°
故答案为:65°
21.32.5°.
【解析】
试题解析:
∵
AB∥CD,∴
∠B+∠BCE
=180°(两直线平行,同旁内角互补)
∵
∠B
=65°,∴
∠BCE
=115°
∵
CM平分∠BCE,∴
∠ECM=∠BCE
=57.5°
∵
∠ECM
+∠MCN
+∠NCD
=180°,∠MCN
=90°
∴
∠NCD
=180°-∠ECM-∠MCN
=180°-57.5°-90°=32.5°.
22.(1)AB∥CD,理由见解析;(2)∠BAE+∠MCD=90°;(3)∠BAC=∠PQC+∠QPC,理由见解析
【详解】
(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+∠MCD=90°;
过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+∠MCD=90°;
(3)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
23.(1)与∠D相等的角为∠DCG,∠ECF,∠B(2)155°(3)25°或155°
【详解】
解:(1)与∠D相等的角为∠DCG,∠ECF,∠B.(1分)理由如下:
∵AD∥BC,
∴∠D=∠DCG.
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG=∠D.
∵AB∥DC,
∴∠B=∠DCG=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B.
(2)∵∠ECF=25°,∠DCE=90°,
∴∠FCD=65°.
又∵∠BCF=90°,
∴∠BCD=65°+90°=155°.
(3)分两种情况进行讨论:
①如图a,当点C在线段BH上时,点F在DA的延长线上,此时∠ECF=∠DCG=∠B=25°.
∵AD∥BC,
∴∠BAF=∠B=25°;
②如图b,当点C在BH的延长线上时,点F在线段AD上.
∵∠B=25°,AD∥BC,
∴∠BAF=180°-25°=155°.
综上所述,∠BAF的度数为25°或155°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
