苏科版 九年级数学下册 第7章 锐角三角函数 单元检测试题(Word版 含解析)
文档属性
| 名称 | 苏科版 九年级数学下册 第7章 锐角三角函数 单元检测试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 184.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 16:20:53 | ||
图片预览


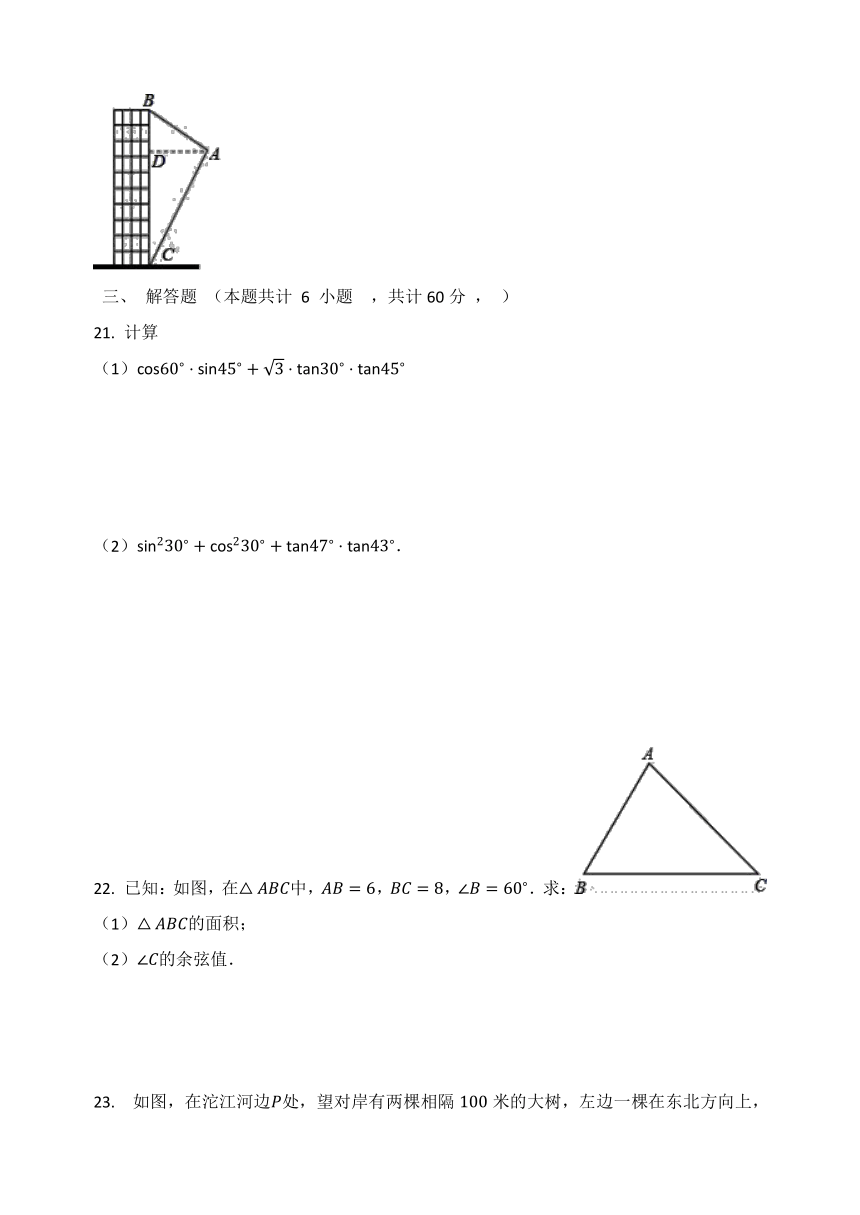
文档简介
1061720010744200123190000第7章 锐角三角函数 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在△ABC中,∠C=90?,AB=5,BC=3,则sinB=( )
A.34 B.35 C.43 D.45
?
2. 计算cos60?-sin30?+tan45?的结果为(? ? ? ? )
A.2 B.-2 C.-1 D.1
?
3. 已知tanα=32,则锐角α所在的范围是( )
A.0?<α<30? B.45?<α<60? C.30?<α<45? D.60?<α<90?
?
4. 在△ABC中,∠C=90?,tanA=13,那么sinA的值是( )
A.12 B.1010 C.33 D.32
?
5. 如图,在△ABC中,BC=12,tanA=34,∠B=30?,则AB长为(? ? ? ? )
A.12 B.14 C.6+63 D.8+63
?
6. 已知:在Rt△ABC中,∠C=90?,sinA=34,则cosB的值为( )
A.74 B.34 C.35 D.45
?
7. 已知:△ABC中,∠A+∠B=90?,下列关系式中成立的式子共有( )
①sinA+B2=cosC2;②tanA+B2=cotC2;③sin(A+B)=sinC;④sin2A+cos2B=1.
A.1个 B.2个 C.3个 D.4个
?
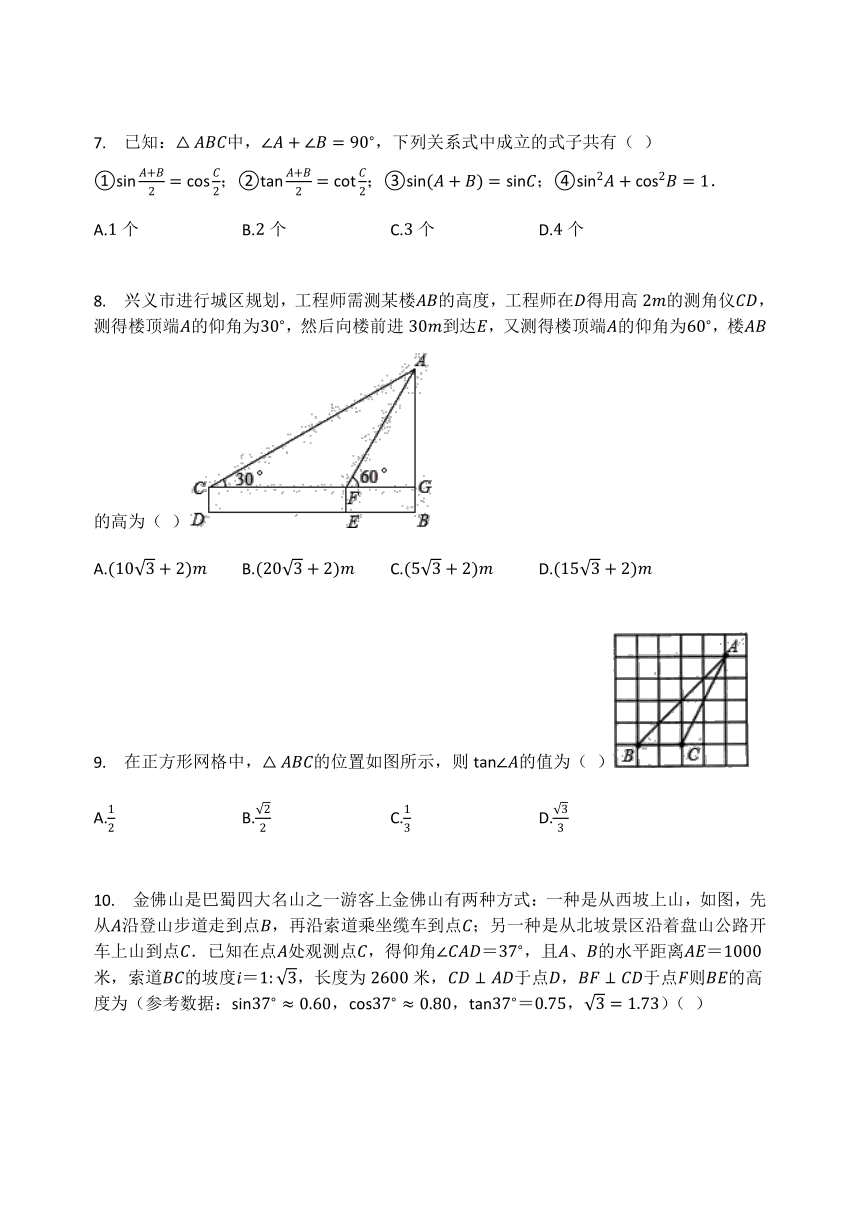
8. 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30?,然后向楼前进30m到达E,又测得楼顶端A的仰角为60?,楼AB的高为( )
A.(103+2)m B.(203+2)m C.(53+2)m D.(153+2)m
?
9. 在正方形网格中,△ABC的位置如图所示,则tan∠A的值为( )
A.12 B.22 C.13 D.33
?
10. 金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37?,且A、B的水平距离AE=1000米,索道BC的坡度i=1:3,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37?≈0.60,cos37?≈0.80,tan37?=0.75,3=1.73)( )
A.2436.8米 B.2249.6米 C.1036.8米 D.1136.8米
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 在△ABC中,∠A、∠B都是锐角,如果sinA=12,cosB=22,那么∠C=________.
?
12. 在△ABC中,∠A=120?,AB=2,AC=4,则sinB的值是________.
?
13. 在△ABC中,∠C=90?,cosB=23,则a﹕b﹕c为________.
?
14. 如图,甲船从A港出发,沿北偏东60?方向航行1000m到达C港,乙船从B港出发,沿西北方向航行2000m到达C港,则S△ABC=________.
?
15. 如图,登山队员在山脚A点测得山顶B点的仰角为∠CAB=45?,当沿倾斜角为30?的斜坡前进100m到达D点以后,又在D点测得山顶B点的仰角为60?,山的高度BC=________.(精确到1米)
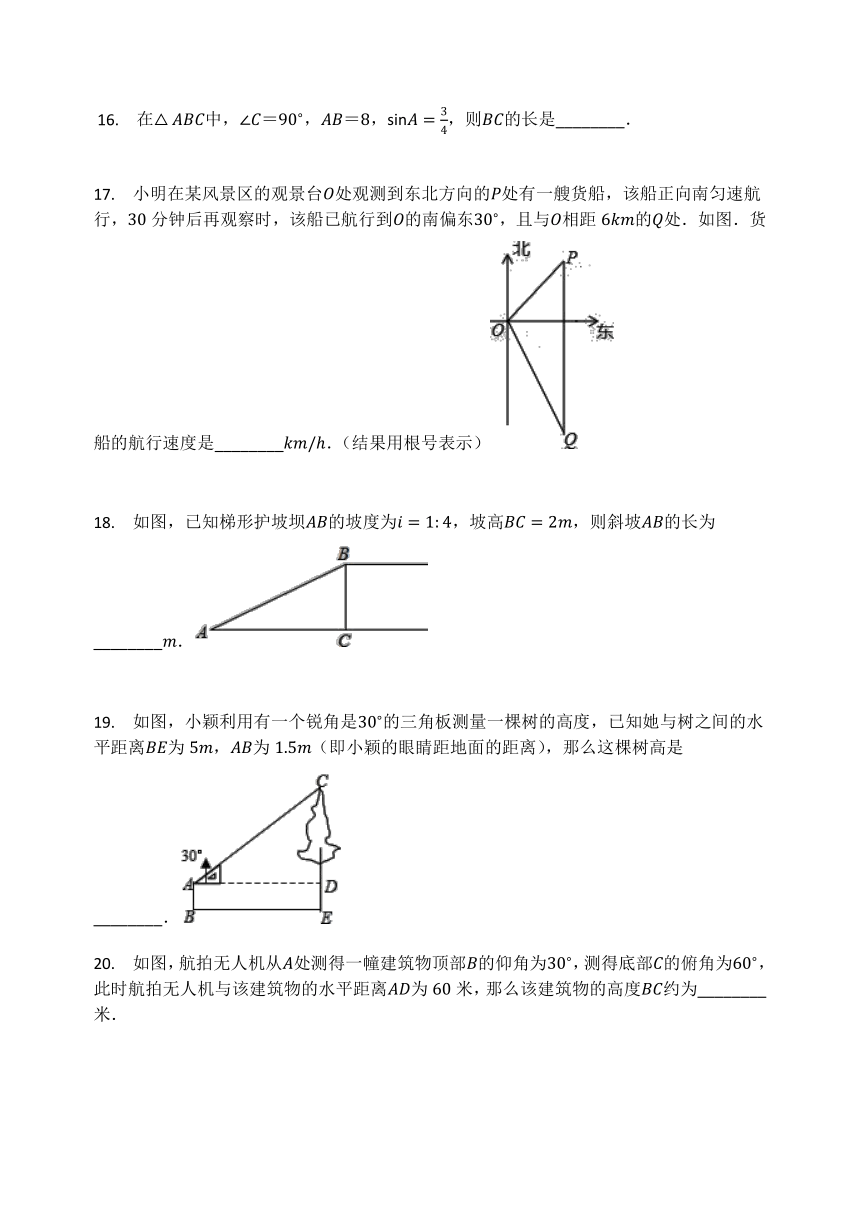
?16. 在△ABC中,∠C=90?,AB=8,sinA=34,则BC的长是________.
?
17. 小明在某风景区的观景台O处观测到东北方向的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东30?,且与O相距6km的Q处.如图.货船的航行速度是________km/h.(结果用根号表示)
?
18. 如图,已知梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,则斜坡AB的长为________m.
?
19. 如图,小颖利用有一个锐角是30?的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是________.
20. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30?,测得底部C的俯角为60?,此时航拍无人机与该建筑物的水平距离AD为60米,那么该建筑物的高度BC约为________米.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 计算
(1)cos60??sin45?+3?tan30??tan45?
(2)sin230?+cos230?+tan47??tan43?.
?
22. 已知:如图,在△ABC中,AB=6,BC=8,∠B=60?.求:
(1)△ABC的面积;
(2)∠C的余弦值.
?
23. 如图,在沱江河边P处,望对岸有两棵相隔100米的大树,左边一棵在东北方向上,右边一棵在北偏东60?方向上,请帮忙计算沱江河宽.(结果保留根号)
?
24. 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而________.
?
25. 如图,某场馆门前的台阶的总高度CB为0.9m,为了方便残疾人行走,该场馆决定将其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为8?,请计算从斜坡起点A到台阶最高点D的距离(即斜坡AD的长).结果精确到0.1m,参考数据:sin8?≈0.14,cos8?≈0.99,tan8?≈0.14)
?26. 2020年汛期过后,省防汛指挥部决定对一段重点堤段的背水坡面进行加固加宽.具体的方案是:将原背水坡AB的坡度i=1:1变为加固后背水坡EF的坡度α=40?,如图,若AE//BF,AE=1米,原背水坡AB=102米.求需要加固的堤坝底部BF的长(精确到0.1米)?(参考数据:sin40?≈0.64,cos40?≈0.77,tan40?≈0.84)
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:∵ ∠C=90?,AB=5,BC=3,
∴ AC=AB2-BC2=4,
∴ sinB=ACAB=45.
故选:D.
2.
【答案】
D
【解答】
原式=12-12+1=1.
故选D.
3.
【答案】
B
【解答】
解:∵ tan60?=3,tan45?=1,1∴ 45?<α<60?.
故选B.
4.
【答案】
B
【解答】
解:tanA=BCAC=13,BC=x,AC=3x,
由勾股定理,得
AB=10x,
sinA=BCAB=1010,
故选:B.
5.
【答案】
D
【解答】
解:如图,作CH⊥AB于H,
在Rt△BCH,
∵ ∠BHC=90?,∠B=30?,
BC=12,
∴ CH=12BC=6,BH=63,
在Rt△ACH,
∵ tanA=CHAH=34,
∴ AH=8,
∴ AB=8+63.
故选D.
6.
【答案】
B
【解答】
解:在Rt△ABC中,∠C=90?得
∠B+∠A=90?.
由一个角的正弦等于它余角的余弦,得
cosB=sinA=34,
故选:B.
7.
【答案】
C
【解答】
解:①sinA+B2=sin45?=22,cosc2=cos45?=22,故正确;
②tanA+B2=tan45?=1,cotc2=cot45?=1,故正确;
③sin(A+B)=sin(180?-A-B)=sinC,故正确;
④∠A+∠B=90?,sin2A+sin2B=1,故错误.
综上可得①②③正确.
故选C.
8.
【答案】
D
【解答】
解:在Rt△AFG中,tan∠AFG=AGFG,
∴ FG=AGtan∠AFG=AG3,
在Rt△ACG中,tan∠ACG=AGCG,
∴ CG=AGtan∠ACG=3AG.
又∵ CG-FG=30m,
即3AG-AG3=30m,
∴ AG=153m,
∴ AB=(153+2)m.
故选:D.
9.
【答案】
C
【解答】
解:连接CD,
则CD2=2,AC2=4+16=20,AD2=9+9=18
∴ AC2=CD2+AD2,AD=18=32,CD=2
∴ ∠ADC=90?
∴ tan∠A=CDAD=232=13.
故选C.
10.
【答案】
D
【解答】
在Rt△BCF中,∵ BC的坡度i=1:3,
∴ ∠CBF=30?,
∵ BC=2600,
∴ CF=1300,BF=13003,
∵ CD⊥AD于点D,BF⊥CD,BE⊥AD,
∴ 四边形BEDF是矩形,
∴ DE=BF=13003,
∵ AE=1000米,
∴ AD=AE+DE=1000+13003,
∵ ∠CAD=37?,
∴ CD=AD?tan37?=(1000+13003)×0.75=2436.75,
∴ BE=DF=2436.75-1300≈1136.8米,
答:BE的高度为1136.8米.
故选:D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
105?
【解答】
解:∵ sinA=12,cosB=22,
∴ ∠A=30?,∠B=45?,
∴ ∠C=180?-30?-45?=105?.
故答案为:105?.
12.
【答案】
217
【解答】
解:作CD⊥AB于D,如图,
∵ ∠A=120?,
∴ ∠CAD=60?,
在Rt△CAD中,AC=4,
∵ sin∠CAD=sin60?=CDAC,
∴ CD=4×32=23,
∵ cos∠CAD=cos60?=ADAC,
∴ AD=12×4=2,
∴ BD=AB+AD=2+2=4,
在Rt△BDC中,BC=CD2+BD2=(23)2+42=27,
∴ sinB=CDBC=2327=217.
故答案为217.
13.
【答案】
2:5:3
【解答】
解:如图,∵ cosB=BCAB=23,
∴ 可设BC=2k,AB=3k,
∴ AC=AB2-BC2=5k,
∴ a:b:c=2k:5k:3k=2:5:3.
故答案为2:5:3.
14.
【答案】
250000(2+6)m2
【解答】
解:过点C作CD⊥AM,CE⊥BN,垂足分别为D,E,
由题意可得:D、E、C在一条直线上,
∵ ∠DAC=60?,∠EBC=45?,AC=1000m,BC=2000m,
∴ AD=ACcos60?=500(m),DC=ACsin60?=5003(m),
EC=BE=22×2000=10002(m),
∴ S△ABC=S梯形DABE-S△ADC-S△BCE
=12(500+10002)×(5003+10002)-12×500×5003-12×10002×10002
=250000(2+6)(m2)
故答案为:250000(2+6)m2.
15.
【答案】
137
【解答】
解:过D作DE⊥AC于E,作DF⊥BC于F.
∵ ∠BAC=45?,∠ACB=90?,
∴ ∠ABC=45?,
又∵ ∠BDF=60?,
∴ ∠DBF=30?,
∴ ∠DAB=∠DBA=15?,
∴ DB=DA=100,
∵ ∠DAE=30?,
∴ FC=DE=12AD=50,
在△BDF中,sin∠BDF=BFBD,
∴ BF=BD×sin∠BDF=100×32=503,
∴ 山高BC=BF+FC=503+50≈137(米).
故答案为:137.
16.
【答案】
6
【解答】
∵ sinA=BCAB,
∴ BC8=34,
解得BC=6.
17.
【答案】
(6+63)
【解答】
解:如图,在直角△OAQ中,∠OAQ=90?,∠Q=30?,OQ=6km,
∴ OA=12OQ=3km,AQ=3OA=33km.
在直角△OAP中,∠OAP=90?,∠AOP=45?,OA=3km,
∴ PA=OA=3km,
∴ PQ=PA+AQ=(3+33)km,
∴ 货船的航行速度是(3+33)÷12=6+63(km/h).
故答案为(6+63).
18.
【答案】
217
【解答】
解:∵ 梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,
∴ BCAC=14,
∴ AC=8m,
根据勾股定理,得
AB=BC2+AC2=22+82=68=217m.
故答案为:217.
19.
【答案】
103+96m
【解答】
解:过A作AD⊥CE于D.
∵ AB⊥BE,DE⊥BE,AD⊥CE,
∴ 四边形ABED是矩形,
∵ BE=5m,AB=1.5m,
∴ AD=BE=5m,DE=AB=1.5m.
在Rt△ACD中,
∵ ∠CAD=30?,AD=5m,
∴ CD=AD?tan30?=5×33=533,
∴ CE=CD+DE=533+1.5=103+96(m).
答:树高是103+96m.
故答案为103+96m.
20.
【答案】
803
【解答】
由题意可得:tan30?=BDAD=BD60=33,
解得:BD=203(米),
tan60?=DCAD=DC60=3,
解得:DC=603(米),
故该建筑物的高度为:BC=BD+DC=803(米)
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)cos60??sin45?+3?tan30??tan45?
=12×22+3×33×1
=24+1;
(2)sin230?+cos230?+tan47??tan43?
=1+1
=2.
【解答】
解:(1)cos60??sin45?+3?tan30??tan45?
=12×22+3×33×1
=24+1;
(2)sin230?+cos230?+tan47??tan43?
=1+1
=2.
22.
【答案】
解:(1)作AH⊥BC,垂足为点H.
在Rt△ABH中,∵ ∠AHB=90?,∠B=60?,AB=6,
∴ BH=3,AH=33,
∴ S△ABC=12×8×33=123,
(2)∵ BC=8,BH=3,∴ CH=5.?
在Rt△ACH中,∵ AH=33,CH=5,
∴ AC=213.
∴ cosC=CHAC=5213=51326.
【解答】
解:(1)作AH⊥BC,垂足为点H.
在Rt△ABH中,∵ ∠AHB=90?,∠B=60?,AB=6,
∴ BH=3,AH=33,
∴ S△ABC=12×8×33=123,
(2)∵ BC=8,BH=3,∴ CH=5.?
在Rt△ACH中,∵ AH=33,CH=5,
∴ AC=213.
∴ cosC=CHAC=5213=51326.
23.
【答案】
沱江河宽是(50+503)米.
【解答】
解:过点P作PC⊥AB于C,设PC=x米,
由题意可知∠CAB=45?,∠CPA=60?,
∴ AC=CP=x米,∠CBP=30?,
∴ BC=AB+CA=(x+100)米,
角三角形BPC中,tan∠CBP=CPCB=xx+100,
∴ xx+100=33,
解得:x=(50+503).
24.
【答案】
增大.
【解答】
解:(1)∵ CA⊥AO,
∴ △FOA和△EOA均为直角三角形.
∴ tan∠AOF=AFOA,tan∠AOE=EAOA.
∴ tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
25.
【答案】
斜坡AD的长约为6.4m.
【解答】
解:过点D作DE⊥AB于点E,
∵ ∠B=90?,CD?//?AB,∴ DE=CB=0.9
在Rt△ADE中,∵ ∠A=8?,∴ AD=DEsin8?≈0.90.14≈6.4.
26.
【答案】
解:过点A作AM⊥CF于M,过点E作EN⊥CF于N,如图,
则四边形AMNE是矩形,
∴ AE=MN=1,?AM=EN.
∵ i=AM:BM=1:1,
∴ AM=BM,
在Rt△ABM中,由勾股定理得:AM2+BM2=1022,
解得AM=BM=10m,
在Rt△EFN中,∵ tan40?=ENFN,
∴ FN=ENtan40?≈100.84≈11.90m,
∴ BF=FN+MN-BM≈11.90+1-10≈2.9m.
【解答】
解:过点A作AM⊥CF于M,过点E作EN⊥CF于N,如图,
则四边形AMNE是矩形,
∴ AE=MN=1,?AM=EN.
∵ i=AM:BM=1:1,
∴ AM=BM,
在Rt△ABM中,由勾股定理得:AM2+BM2=1022,
解得AM=BM=10m,
在Rt△EFN中,∵ tan40?=ENFN,
∴ FN=ENtan40?≈100.84≈11.90m,
∴ BF=FN+MN-BM≈11.90+1-10≈2.9m.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在△ABC中,∠C=90?,AB=5,BC=3,则sinB=( )
A.34 B.35 C.43 D.45
?
2. 计算cos60?-sin30?+tan45?的结果为(? ? ? ? )
A.2 B.-2 C.-1 D.1
?
3. 已知tanα=32,则锐角α所在的范围是( )
A.0?<α<30? B.45?<α<60? C.30?<α<45? D.60?<α<90?
?
4. 在△ABC中,∠C=90?,tanA=13,那么sinA的值是( )
A.12 B.1010 C.33 D.32
?
5. 如图,在△ABC中,BC=12,tanA=34,∠B=30?,则AB长为(? ? ? ? )
A.12 B.14 C.6+63 D.8+63
?
6. 已知:在Rt△ABC中,∠C=90?,sinA=34,则cosB的值为( )
A.74 B.34 C.35 D.45
?
7. 已知:△ABC中,∠A+∠B=90?,下列关系式中成立的式子共有( )
①sinA+B2=cosC2;②tanA+B2=cotC2;③sin(A+B)=sinC;④sin2A+cos2B=1.
A.1个 B.2个 C.3个 D.4个
?
8. 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30?,然后向楼前进30m到达E,又测得楼顶端A的仰角为60?,楼AB的高为( )
A.(103+2)m B.(203+2)m C.(53+2)m D.(153+2)m
?
9. 在正方形网格中,△ABC的位置如图所示,则tan∠A的值为( )
A.12 B.22 C.13 D.33
?
10. 金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37?,且A、B的水平距离AE=1000米,索道BC的坡度i=1:3,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37?≈0.60,cos37?≈0.80,tan37?=0.75,3=1.73)( )
A.2436.8米 B.2249.6米 C.1036.8米 D.1136.8米
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 在△ABC中,∠A、∠B都是锐角,如果sinA=12,cosB=22,那么∠C=________.
?
12. 在△ABC中,∠A=120?,AB=2,AC=4,则sinB的值是________.
?
13. 在△ABC中,∠C=90?,cosB=23,则a﹕b﹕c为________.
?
14. 如图,甲船从A港出发,沿北偏东60?方向航行1000m到达C港,乙船从B港出发,沿西北方向航行2000m到达C港,则S△ABC=________.
?
15. 如图,登山队员在山脚A点测得山顶B点的仰角为∠CAB=45?,当沿倾斜角为30?的斜坡前进100m到达D点以后,又在D点测得山顶B点的仰角为60?,山的高度BC=________.(精确到1米)
?16. 在△ABC中,∠C=90?,AB=8,sinA=34,则BC的长是________.
?
17. 小明在某风景区的观景台O处观测到东北方向的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东30?,且与O相距6km的Q处.如图.货船的航行速度是________km/h.(结果用根号表示)
?
18. 如图,已知梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,则斜坡AB的长为________m.
?
19. 如图,小颖利用有一个锐角是30?的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是________.
20. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30?,测得底部C的俯角为60?,此时航拍无人机与该建筑物的水平距离AD为60米,那么该建筑物的高度BC约为________米.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 计算
(1)cos60??sin45?+3?tan30??tan45?
(2)sin230?+cos230?+tan47??tan43?.
?
22. 已知:如图,在△ABC中,AB=6,BC=8,∠B=60?.求:
(1)△ABC的面积;
(2)∠C的余弦值.
?
23. 如图,在沱江河边P处,望对岸有两棵相隔100米的大树,左边一棵在东北方向上,右边一棵在北偏东60?方向上,请帮忙计算沱江河宽.(结果保留根号)
?
24. 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而________.
?
25. 如图,某场馆门前的台阶的总高度CB为0.9m,为了方便残疾人行走,该场馆决定将其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为8?,请计算从斜坡起点A到台阶最高点D的距离(即斜坡AD的长).结果精确到0.1m,参考数据:sin8?≈0.14,cos8?≈0.99,tan8?≈0.14)
?26. 2020年汛期过后,省防汛指挥部决定对一段重点堤段的背水坡面进行加固加宽.具体的方案是:将原背水坡AB的坡度i=1:1变为加固后背水坡EF的坡度α=40?,如图,若AE//BF,AE=1米,原背水坡AB=102米.求需要加固的堤坝底部BF的长(精确到0.1米)?(参考数据:sin40?≈0.64,cos40?≈0.77,tan40?≈0.84)
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:∵ ∠C=90?,AB=5,BC=3,
∴ AC=AB2-BC2=4,
∴ sinB=ACAB=45.
故选:D.
2.
【答案】
D
【解答】
原式=12-12+1=1.
故选D.
3.
【答案】
B
【解答】
解:∵ tan60?=3,tan45?=1,1
故选B.
4.
【答案】
B
【解答】
解:tanA=BCAC=13,BC=x,AC=3x,
由勾股定理,得
AB=10x,
sinA=BCAB=1010,
故选:B.
5.
【答案】
D
【解答】
解:如图,作CH⊥AB于H,
在Rt△BCH,
∵ ∠BHC=90?,∠B=30?,
BC=12,
∴ CH=12BC=6,BH=63,
在Rt△ACH,
∵ tanA=CHAH=34,
∴ AH=8,
∴ AB=8+63.
故选D.
6.
【答案】
B
【解答】
解:在Rt△ABC中,∠C=90?得
∠B+∠A=90?.
由一个角的正弦等于它余角的余弦,得
cosB=sinA=34,
故选:B.
7.
【答案】
C
【解答】
解:①sinA+B2=sin45?=22,cosc2=cos45?=22,故正确;
②tanA+B2=tan45?=1,cotc2=cot45?=1,故正确;
③sin(A+B)=sin(180?-A-B)=sinC,故正确;
④∠A+∠B=90?,sin2A+sin2B=1,故错误.
综上可得①②③正确.
故选C.
8.
【答案】
D
【解答】
解:在Rt△AFG中,tan∠AFG=AGFG,
∴ FG=AGtan∠AFG=AG3,
在Rt△ACG中,tan∠ACG=AGCG,
∴ CG=AGtan∠ACG=3AG.
又∵ CG-FG=30m,
即3AG-AG3=30m,
∴ AG=153m,
∴ AB=(153+2)m.
故选:D.
9.
【答案】
C
【解答】
解:连接CD,
则CD2=2,AC2=4+16=20,AD2=9+9=18
∴ AC2=CD2+AD2,AD=18=32,CD=2
∴ ∠ADC=90?
∴ tan∠A=CDAD=232=13.
故选C.
10.
【答案】
D
【解答】
在Rt△BCF中,∵ BC的坡度i=1:3,
∴ ∠CBF=30?,
∵ BC=2600,
∴ CF=1300,BF=13003,
∵ CD⊥AD于点D,BF⊥CD,BE⊥AD,
∴ 四边形BEDF是矩形,
∴ DE=BF=13003,
∵ AE=1000米,
∴ AD=AE+DE=1000+13003,
∵ ∠CAD=37?,
∴ CD=AD?tan37?=(1000+13003)×0.75=2436.75,
∴ BE=DF=2436.75-1300≈1136.8米,
答:BE的高度为1136.8米.
故选:D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
105?
【解答】
解:∵ sinA=12,cosB=22,
∴ ∠A=30?,∠B=45?,
∴ ∠C=180?-30?-45?=105?.
故答案为:105?.
12.
【答案】
217
【解答】
解:作CD⊥AB于D,如图,
∵ ∠A=120?,
∴ ∠CAD=60?,
在Rt△CAD中,AC=4,
∵ sin∠CAD=sin60?=CDAC,
∴ CD=4×32=23,
∵ cos∠CAD=cos60?=ADAC,
∴ AD=12×4=2,
∴ BD=AB+AD=2+2=4,
在Rt△BDC中,BC=CD2+BD2=(23)2+42=27,
∴ sinB=CDBC=2327=217.
故答案为217.
13.
【答案】
2:5:3
【解答】
解:如图,∵ cosB=BCAB=23,
∴ 可设BC=2k,AB=3k,
∴ AC=AB2-BC2=5k,
∴ a:b:c=2k:5k:3k=2:5:3.
故答案为2:5:3.
14.
【答案】
250000(2+6)m2
【解答】
解:过点C作CD⊥AM,CE⊥BN,垂足分别为D,E,
由题意可得:D、E、C在一条直线上,
∵ ∠DAC=60?,∠EBC=45?,AC=1000m,BC=2000m,
∴ AD=ACcos60?=500(m),DC=ACsin60?=5003(m),
EC=BE=22×2000=10002(m),
∴ S△ABC=S梯形DABE-S△ADC-S△BCE
=12(500+10002)×(5003+10002)-12×500×5003-12×10002×10002
=250000(2+6)(m2)
故答案为:250000(2+6)m2.
15.
【答案】
137
【解答】
解:过D作DE⊥AC于E,作DF⊥BC于F.
∵ ∠BAC=45?,∠ACB=90?,
∴ ∠ABC=45?,
又∵ ∠BDF=60?,
∴ ∠DBF=30?,
∴ ∠DAB=∠DBA=15?,
∴ DB=DA=100,
∵ ∠DAE=30?,
∴ FC=DE=12AD=50,
在△BDF中,sin∠BDF=BFBD,
∴ BF=BD×sin∠BDF=100×32=503,
∴ 山高BC=BF+FC=503+50≈137(米).
故答案为:137.
16.
【答案】
6
【解答】
∵ sinA=BCAB,
∴ BC8=34,
解得BC=6.
17.
【答案】
(6+63)
【解答】
解:如图,在直角△OAQ中,∠OAQ=90?,∠Q=30?,OQ=6km,
∴ OA=12OQ=3km,AQ=3OA=33km.
在直角△OAP中,∠OAP=90?,∠AOP=45?,OA=3km,
∴ PA=OA=3km,
∴ PQ=PA+AQ=(3+33)km,
∴ 货船的航行速度是(3+33)÷12=6+63(km/h).
故答案为(6+63).
18.
【答案】
217
【解答】
解:∵ 梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,
∴ BCAC=14,
∴ AC=8m,
根据勾股定理,得
AB=BC2+AC2=22+82=68=217m.
故答案为:217.
19.
【答案】
103+96m
【解答】
解:过A作AD⊥CE于D.
∵ AB⊥BE,DE⊥BE,AD⊥CE,
∴ 四边形ABED是矩形,
∵ BE=5m,AB=1.5m,
∴ AD=BE=5m,DE=AB=1.5m.
在Rt△ACD中,
∵ ∠CAD=30?,AD=5m,
∴ CD=AD?tan30?=5×33=533,
∴ CE=CD+DE=533+1.5=103+96(m).
答:树高是103+96m.
故答案为103+96m.
20.
【答案】
803
【解答】
由题意可得:tan30?=BDAD=BD60=33,
解得:BD=203(米),
tan60?=DCAD=DC60=3,
解得:DC=603(米),
故该建筑物的高度为:BC=BD+DC=803(米)
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)cos60??sin45?+3?tan30??tan45?
=12×22+3×33×1
=24+1;
(2)sin230?+cos230?+tan47??tan43?
=1+1
=2.
【解答】
解:(1)cos60??sin45?+3?tan30??tan45?
=12×22+3×33×1
=24+1;
(2)sin230?+cos230?+tan47??tan43?
=1+1
=2.
22.
【答案】
解:(1)作AH⊥BC,垂足为点H.
在Rt△ABH中,∵ ∠AHB=90?,∠B=60?,AB=6,
∴ BH=3,AH=33,
∴ S△ABC=12×8×33=123,
(2)∵ BC=8,BH=3,∴ CH=5.?
在Rt△ACH中,∵ AH=33,CH=5,
∴ AC=213.
∴ cosC=CHAC=5213=51326.
【解答】
解:(1)作AH⊥BC,垂足为点H.
在Rt△ABH中,∵ ∠AHB=90?,∠B=60?,AB=6,
∴ BH=3,AH=33,
∴ S△ABC=12×8×33=123,
(2)∵ BC=8,BH=3,∴ CH=5.?
在Rt△ACH中,∵ AH=33,CH=5,
∴ AC=213.
∴ cosC=CHAC=5213=51326.
23.
【答案】
沱江河宽是(50+503)米.
【解答】
解:过点P作PC⊥AB于C,设PC=x米,
由题意可知∠CAB=45?,∠CPA=60?,
∴ AC=CP=x米,∠CBP=30?,
∴ BC=AB+CA=(x+100)米,
角三角形BPC中,tan∠CBP=CPCB=xx+100,
∴ xx+100=33,
解得:x=(50+503).
24.
【答案】
增大.
【解答】
解:(1)∵ CA⊥AO,
∴ △FOA和△EOA均为直角三角形.
∴ tan∠AOF=AFOA,tan∠AOE=EAOA.
∴ tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
25.
【答案】
斜坡AD的长约为6.4m.
【解答】
解:过点D作DE⊥AB于点E,
∵ ∠B=90?,CD?//?AB,∴ DE=CB=0.9
在Rt△ADE中,∵ ∠A=8?,∴ AD=DEsin8?≈0.90.14≈6.4.
26.
【答案】
解:过点A作AM⊥CF于M,过点E作EN⊥CF于N,如图,
则四边形AMNE是矩形,
∴ AE=MN=1,?AM=EN.
∵ i=AM:BM=1:1,
∴ AM=BM,
在Rt△ABM中,由勾股定理得:AM2+BM2=1022,
解得AM=BM=10m,
在Rt△EFN中,∵ tan40?=ENFN,
∴ FN=ENtan40?≈100.84≈11.90m,
∴ BF=FN+MN-BM≈11.90+1-10≈2.9m.
【解答】
解:过点A作AM⊥CF于M,过点E作EN⊥CF于N,如图,
则四边形AMNE是矩形,
∴ AE=MN=1,?AM=EN.
∵ i=AM:BM=1:1,
∴ AM=BM,
在Rt△ABM中,由勾股定理得:AM2+BM2=1022,
解得AM=BM=10m,
在Rt△EFN中,∵ tan40?=ENFN,
∴ FN=ENtan40?≈100.84≈11.90m,
∴ BF=FN+MN-BM≈11.90+1-10≈2.9m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
