苏科版九年级数学下册 第6章 图形的相似 单元检测试题(Word版 有答案)
文档属性
| 名称 | 苏科版九年级数学下册 第6章 图形的相似 单元检测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 16:19:59 | ||
图片预览

文档简介
1061720010744200123190000第6章 图形的相似 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 若ab=52,则a+ba=( )
A.35 B.32 C.75 D.72
?
2. 如果mn=ab,那么下列比例式中错误的是(? ? ? ? )
A.am=nb B.an=mb C.ma=nb D.ma=bn
?
3. 点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于(? ? ? ? )
A.6cm B.(55+1)cm C.5(5-1)cm D.(55-1)cm
?
4. 如图,在△ABC中,∠BAC=90?,AD⊥BC,垂足为D,DE⊥AB,垂足为E,则图中与△ADE相似的三角形个数为(? ? ? ? )
A.1 B.2 C.3 D.4
?
5. 下列结论错误的是( )
A.等边三角形都相似 B.正方形都相似
C.所有长方形都相似 D.等腰直角三角形都相似
?
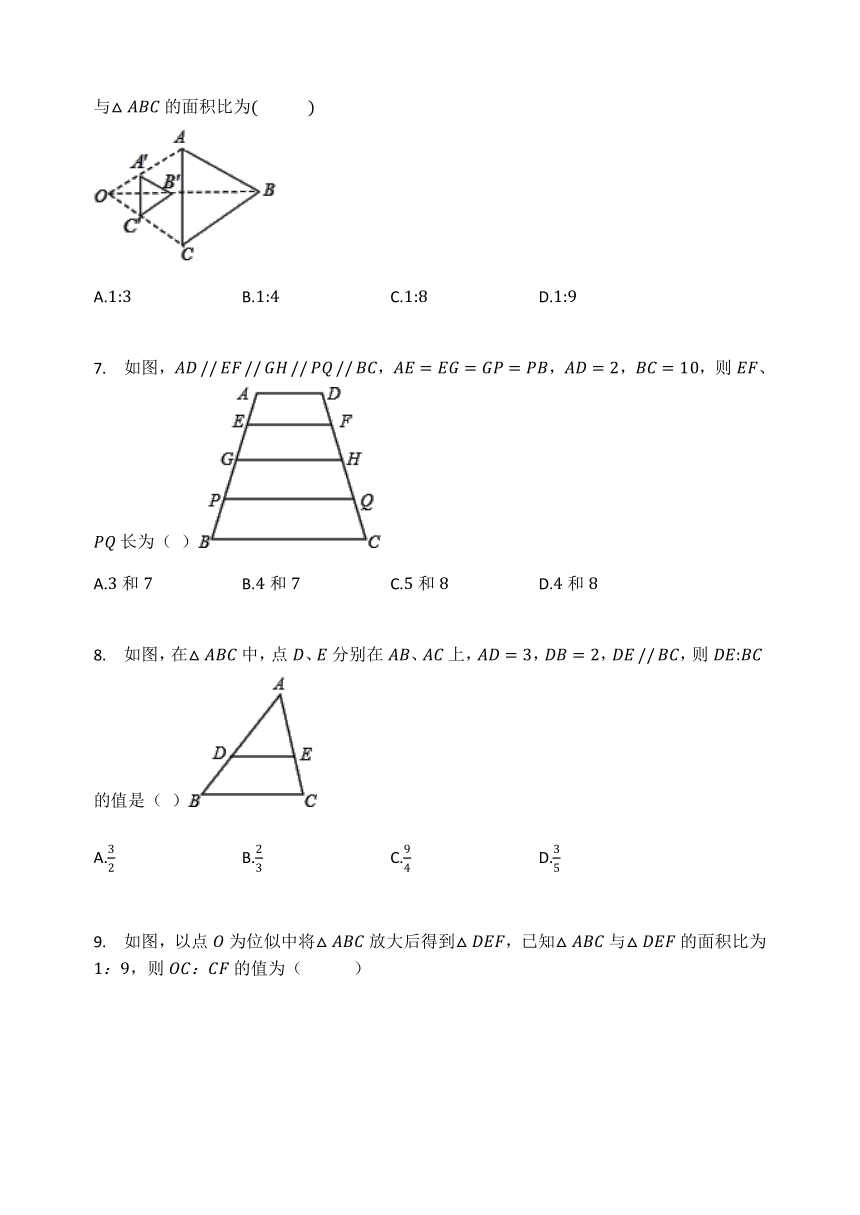
6. 如图,以点O为位似中心,将△ABC缩小后得到△A'B'C',已知OB=3OB',则△A'B'C'与△ABC的面积比为(? ? ? ? )
A.1:3 B.1:4 C.1:8 D.1:9
?
7. 如图,AD?//?EF?//?GH?//?PQ?//?BC,AE=EG=GP=PB,AD=2,BC=10,则EF、PQ长为( )
A.3和7 B.4和7 C.5和8 D.4和8
?
8. 如图,在△ABC中,点D、E分别在AB、AC上,AD=3,DB=2,DE?//?BC,则DE:BC的值是( )
A.32 B.23 C.94 D.35
?
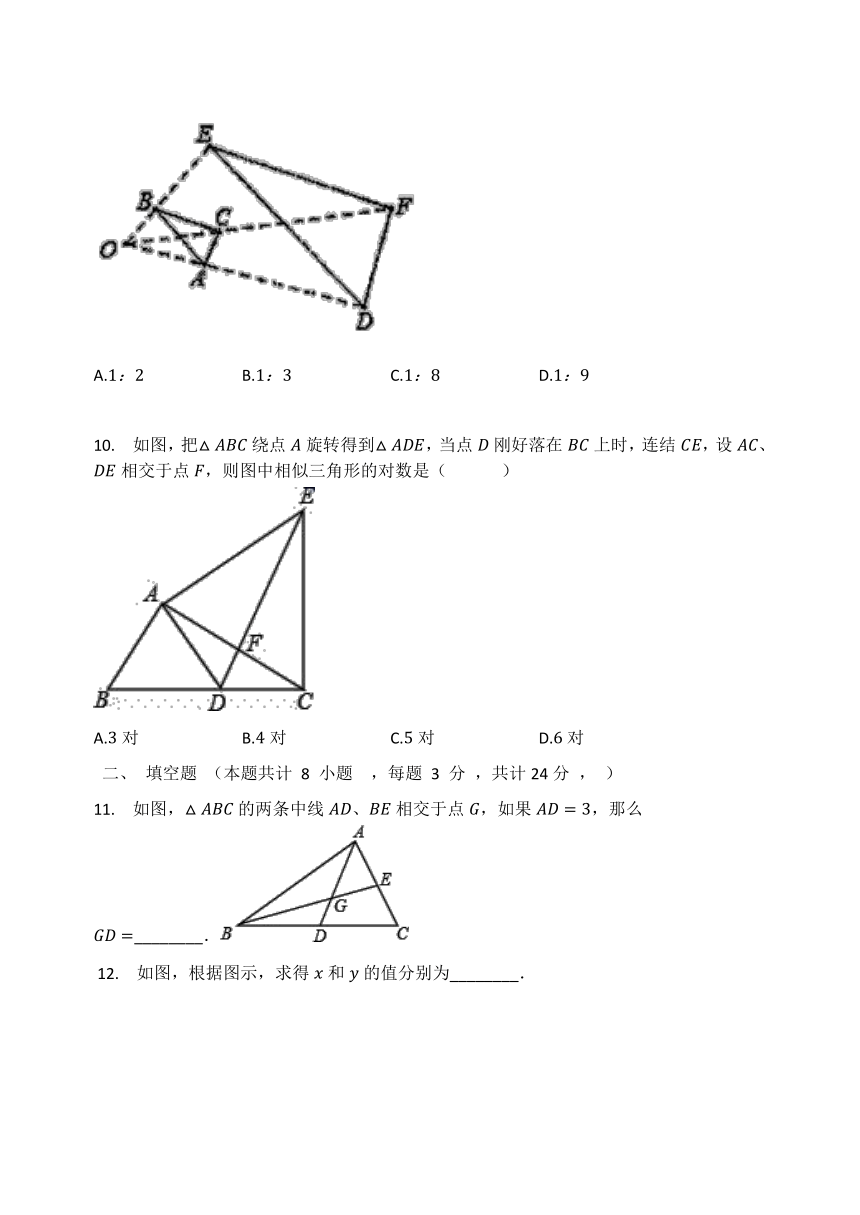
9. 如图,以点O为位似中将△ABC放大后得到△DEF,已知△ABC与△DEF的面积比为1:9,则OC:CF的值为(? ? ? ? )
A.1:2 B.1:3 C.1:8 D.1:9
?
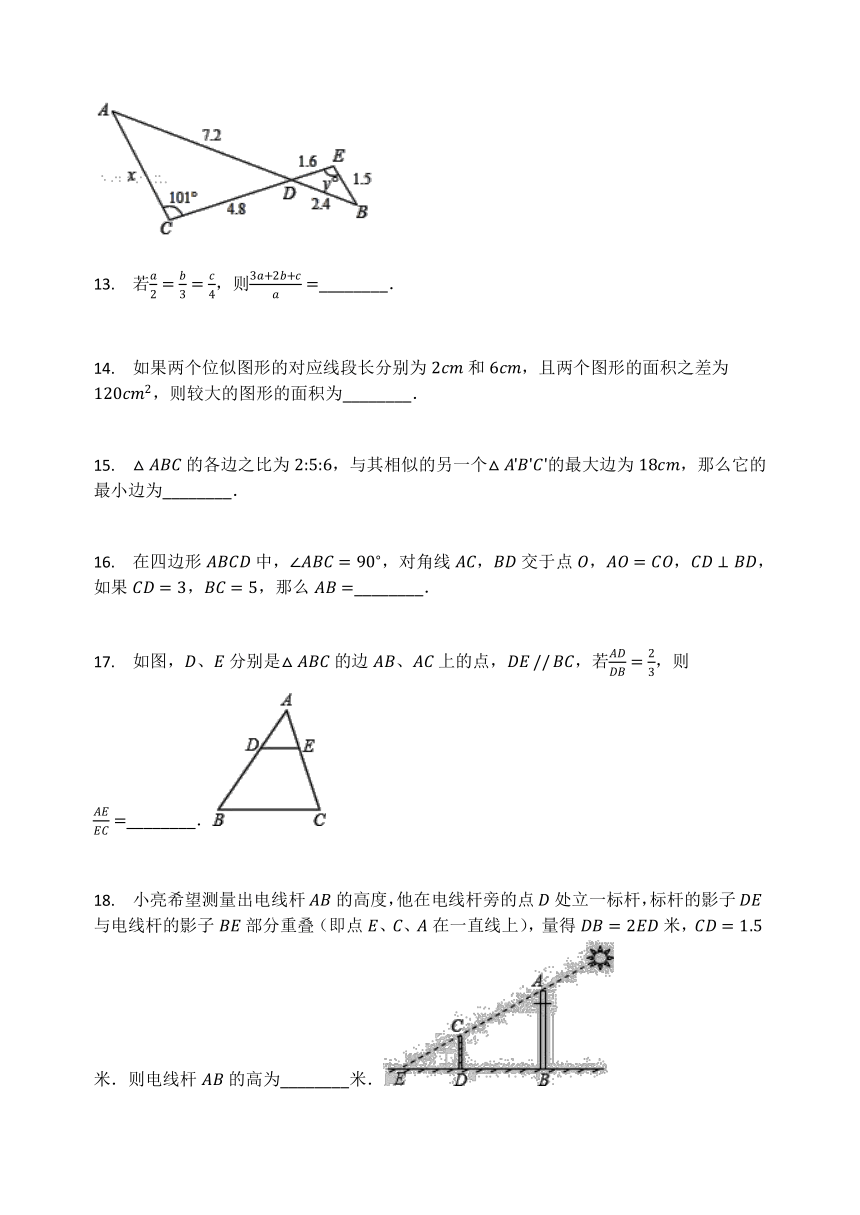
10. 如图,把△ABC绕点A旋转得到△ADE,当点D刚好落在BC上时,连结CE,设AC、DE相交于点F,则图中相似三角形的对数是(? ? ? ? ?)
A.3对 B.4对 C.5对 D.6对
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
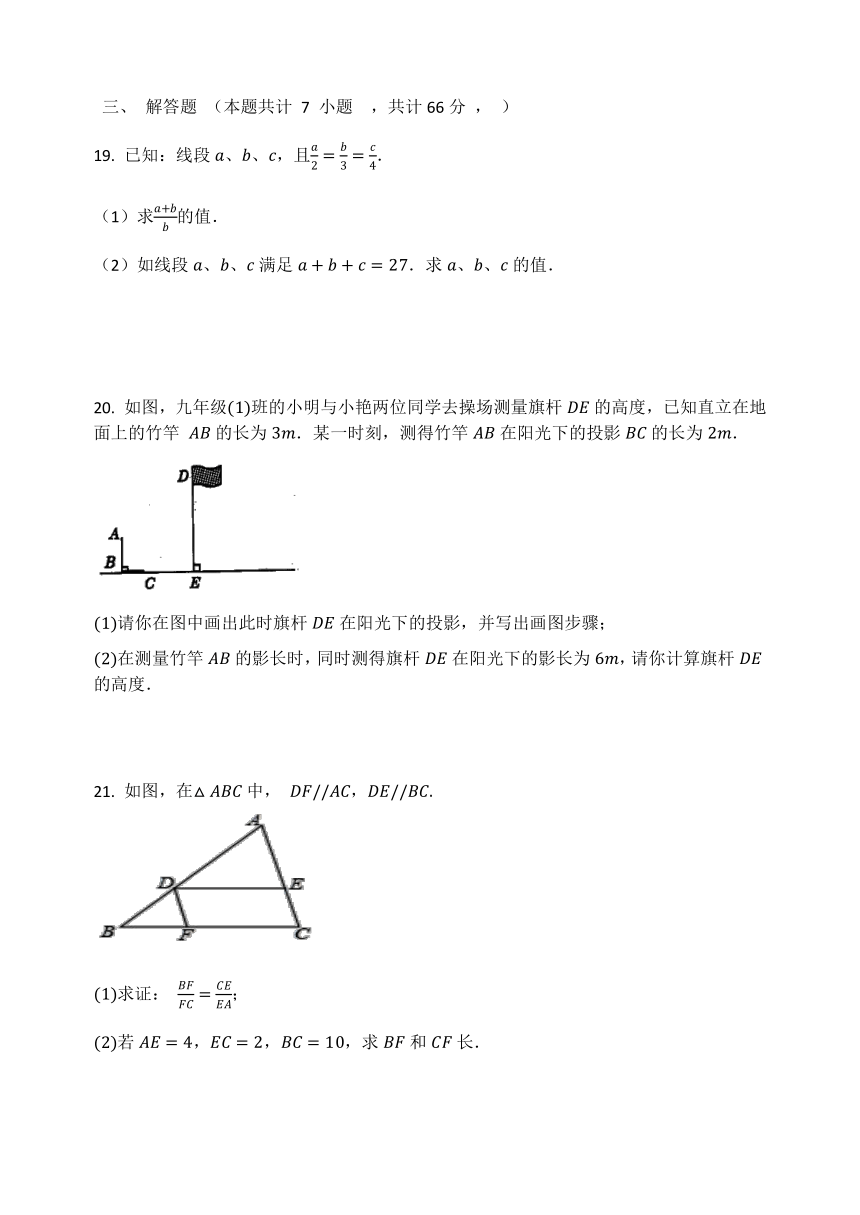
11. 如图,△ABC的两条中线AD、BE相交于点G,如果AD=3,那么GD=________.
?12. 如图,根据图示,求得x和y的值分别为________.
?
13. 若a2=b3=c4,则3a+2b+ca=________.
?
14. 如果两个位似图形的对应线段长分别为2cm和6cm,且两个图形的面积之差为120cm2,则较大的图形的面积为________.
?
15. △ABC的各边之比为2:5:6,与其相似的另一个△A'B'C'的最大边为18cm,那么它的最小边为________.
?
16. 在四边形ABCD中,∠ABC=90?,对角线AC,BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=________.
?
17. 如图,D、E分别是△ABC的边AB、AC上的点,DE?//?BC,若ADDB=23,则AEEC=________.
?
18. 小亮希望测量出电线杆AB的高度,他在电线杆旁的点D处立一标杆,标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得DB=2ED米,CD=1.5米.则电线杆AB的高为________米.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 已知:线段a、b、c,且a2=b3=c4.
(1)求a+bb的值.
(2)如线段a、b、c满足a+b+c=27.求a、b、c的值.
?
20. 如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿 AB的长为3m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6m,请你计算旗杆DE的高度.
?
21. 如图,在△ABC中, DF//AC,DE//BC.
(1)求证: BFFC=CEEA;
(2)若AE=4,EC=2,BC=10,求BF和CF长.
?
22. 如图,在△AMC中,已知BD?//?CM,AC+AB=14,且AM:AD=4:3,求AB的长.
?
23. 如图,四边形OABC与四边形OA'B'C'是位似图形,AB与A'B'一定平行吗?为什么?
?
24. 某市在一道路拓宽改造过程中,发现原来道路两边的路灯除照亮路面的圆的面积不能满足需求外,亮度效果足以满图拓宽后的设计标准,因此,经设计人员研究,只要将路灯的灯标增加一定高度,使其照亮路面圆的面积为原来的2倍即可.已知原来路灯灯高为7.5米,请你求出原灯杆至少再增加多少米,才能符合拓宽后的设计要求?(精确到0.1米)
?
25. 如图,△ABC中,∠C=90?,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=13CD,过点B作BF?//?DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)求BF的长;
(3)若点P是射线BG上的一点,当BP的长为多少时,△BCP与△BCD相似?并说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
a+ba=1+ba
∵ ab=52
∴ ba=25
把ba=25代入a+ba=1+ba=75
2.
【答案】
C
【解答】
解:A、由am=nb得,ab=mn,故本选项不符合题意;
B、由an=mb得,ab=mn,故本选项不符合题意;
C、由ma=nb得,bm=an,故本选项符合题意;
D、由ma=bn得,ab=mn,故本选项不符合题意.
故选C.
3.
【答案】
C
【解答】
解:∵ 点C是线段AB的黄金分割点(AC>BC),
∴ AC=5-12AB,
而AB=10cm,
∴ AC=5-12×10=5(5-1)cm.
故选C.
4.
【答案】
D
【解答】
解:∵ AD⊥BC,DE⊥BA,
∴ ∠ADC=∠AED=90?,
∵ ∠BAC=90?,
∴ DE?//?AC,
∴ ∠ADE=∠DAC,
∴ △ADE?△CAD,
∴ ∠DAE=∠C,
∴ △ADE?△BAC,
∵ DE?//?AC,
∴ ∠BDE=∠C,
∴ △ADE?△BED.
∵ ∠AED=∠ADB=90?,
∴ △ADE?△ABD.
故选D.
5.
【答案】
C
【解答】
解:A、等边三角形都相似,正确,不合题意;
B、正方形都相似,正确,不合题意;
C、所有长方形不一定相似,故此选项错误,符合题意;
D、等腰直角三角形都相似,正确,不合题意;
故选:C.
6.
【答案】
D
【解答】
解:由位似变换的性质可知,A'B'?//?AB,A'C'?//?AC,
∴ OA'OA=OB'OB=13,
∴ A'C'AC=OA'OA=13,
∴ △A'B'C'与△ABC的相似比为1:3,
∴ △A'B'C'与△ABC的面积比为1:9,
故选D.
7.
【答案】
D
【解答】
解:过点D作DM?//?AB,交BC于点M,交EF、GH、PQ分别于点N、K、O,如下图所示:
∵ AD?//?BC,AB?//?DM,
∴ ABMD为平行四边形,
又AD?//?EF?//?GH?//?PQ?//?BC,
同理得到四边形AEND、AGKD、APOD都为平行四边形,
∴ AD=BM=EN=PO=2,
∴ CM=8,
∵ EF?//?BC,PQ?//?BC,AE=EG=GP=PB,
∴ NFMC=DFDC=14,OQCM=DQDC=34,
∴ NF=2,OQ=6,
∴ EF=EN+NF=4,PQ=PO+OQ=8.
故选D.
8.
【答案】
D
【解答】
解:∵ AD=3,DB=2,
∴ AB=AD+BD=3+2=5,
∵ DE?//?BC,
∴ DE:BC=AD:AB=3:5.
故选D.
9.
【答案】
A
【解答】
此题暂无解答
10.
【答案】
B
【解答】
解:∵ △ABC绕点A旋转得△ADE,
∴ △ABC?△ADE,∠AED=∠ACB,
∴ ∠EAF=∠FDC,
又∵ ∠AFE=∠DFC,
∴ △AFE?△DFC,
∴ AFDF=EFFC,
∵ ∠AFD=∠EFC,
∴ △AFD?△EFC,
∵ △ABC?△ADE,
∴ ∠BAC=∠DAE,AB=AD,AC=AE,
∴ ∠EAC=∠BAD,
∴ △AEC?△ABD.
∴ 共有4对相似三角形.
故选B.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
1
【解答】
解:∵ △ABC的两条中线AD、BE相交于点G,AD=3,
∴ 2GD=AG,
∴ GD=1,
故答案为:1.
12.
【答案】
4.5,101
【解答】
由图形可知:4.81.6=7.22.4=3,
∠ADC=∠BDE,
∴ △ADC∽△BDE,
∴ x1.5=3,
∴ x=4.5,
∠C=∠E=101?,
13.
【答案】
8
【解答】
解:根据题意,设a=2k,则b=3k,c=4k,
∴ 3a+2b+ca=6k+6k+4k2k=8.
14.
【答案】
135cm2
【解答】
解:∵ 两个位似图形的对应线段长分别为2cm和6cm,
∴ 其面积比为22:62=1:9,
∴ 设两正六边形的面积分别为x和9x,
根据题意列方程得,9x-x=120,
即8x=120,
解得:x=15.
则较大的图形的面积为:9×15=153(cm2).
故答案为:135cm2.
15.
【答案】
6cm
【解答】
解:∵ △ABC∽△A'B'C',△ABC的各边之比为2:5:6,
∴ △A'B'C'的各边之比为2:5:6,
∵ △A'B'C'的最大边为18cm,
∴ △A'B'C'的最小边为6cm.
16.
【答案】
154
【解答】
解:如图,过点A作AE⊥BD.
∵ CD⊥BD,AE⊥BD,
∴ ∠CDB=∠AED=90?,且AO=CO,∠COD=∠AOE,
∴ △AOE?△COD(AAS),
∴ CD=AE=3.
∵ ∠CDB=90?,CD=3,BC=5,
∴ DB?=?BC?2?-?CD?2?=?25?-?9?=?4.
∵ ∠ABC=∠AEB=90?,
∴ ∠ABE+∠EAB=90?,∠CBD+∠ABE=90?,
∴ ∠EAB=∠CBD,且∠CDB=∠AEB=90?,
∴ △ABE?△BCD,
∴ AEBD?=?ABBC,
∴ 34?=?AB5,
∴ AB?=?154.
故答案为:154.
17.
【答案】
23
【解答】
解:∵ DE?//?BC
∴ AEEC=ADDB=23.
18.
【答案】
4.5
【解答】
解:∵ CD?//?AB,
∴ △ECD∽△EAB,
∴ EDEB=CDAB,
∴ 13=1.5AB,
∴ AB=4.5(米).
故答案为;4.5.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:(1)∵ a2=b3,
∴ ab=23,
∴ a+bb=53,
(2)设a2=b3=c4=k,
则a=2k,b=3k,c=4k,
∵ a+b+c=27,
∴ 2k+3k+4k=27,
∴ k=3,
∴ a=6,b=9,c=12.
【解答】
解:(1)∵ a2=b3,
∴ ab=23,
∴ a+bb=53,
(2)设a2=b3=c4=k,
则a=2k,b=3k,c=4k,
∵ a+b+c=27,
∴ 2k+3k+4k=27,
∴ k=3,
∴ a=6,b=9,c=12.
20.
【答案】
解:(1)如图,线段EF就是旗杆DE在阳光下的投影.
作法:连接AC,过点D作DF//AC,交直线BE于点F,线段EF即为所求.
(2)∵ AC//DF,
∴ ∠ACB=∠DFE.
又∠ABC=∠DEF=90?,
∴ △ABC?△DEF,
∴ ABDE=BCEF.
∵ AB=3m,BC=2m,EF=6m,
∴ 3DE=26,
∴ DE=9m,
∴ 旗杆DE的高度为9m.
【解答】
解:(1)如图,线段EF就是旗杆DE在阳光下的投影.
作法:连接AC,过点D作DF//AC,交直线BE于点F,线段EF即为所求.
(2)∵ AC//DF,
∴ ∠ACB=∠DFE.
又∠ABC=∠DEF=90?,
∴ △ABC?△DEF,
∴ ABDE=BCEF.
∵ AB=3m,BC=2m,EF=6m,
∴ 3DE=26,
∴ DE=9m,
∴ 旗杆DE的高度为9m.
21.
【答案】
解:(1)∵ ?DF//AC,
∴ ?BFFC=BDDA.
∵ ?DE//BC,
∴ ?CEEA=BDDA,
∴ ?BFFC=CEEA.
(2)设BF=x,则CF=10-x.
由(1)得:BFFC=CEEA,
∴ ?x10-x=24,x=103,
∴ BF=103,CF=10-103=203.
【解答】
解:(1)∵ ?DF//AC,
∴ ?BFFC=BDDA.
∵ ?DE//BC,
∴ ?CEEA=BDDA,
∴ ?BFFC=CEEA.
(2)设BF=x,则CF=10-x.
由(1)得:BFFC=CEEA,
∴ ?x10-x=24,x=103,
∴ BF=103,CF=10-103=203.
22.
【答案】
解:∵ BD?//?CM,
∴ AC:AB=AM:AD=4:3,
∵ AC+AB=14,
∴ AC=47×14=8,AB=37×14=6,
∴ AB的长为6.
【解答】
解:∵ BD?//?CM,
∴ AC:AB=AM:AD=4:3,
∵ AC+AB=14,
∴ AC=47×14=8,AB=37×14=6,
∴ AB的长为6.
23.
【答案】
解:AB与A'B'一定平行,
∵ 四边形OABC与四边形OA'B'C'是位似图形,
∴ 四边形OABC∽四边形OA'B'C',
∴ ∠OAB=∠OA'B',
∴ AB?//?A'B'.
【解答】
解:AB与A'B'一定平行,
∵ 四边形OABC与四边形OA'B'C'是位似图形,
∴ 四边形OABC∽四边形OA'B'C',
∴ ∠OAB=∠OA'B',
∴ AB?//?A'B'.
24.
【答案】
由题意可得:△AOB∽△A'OB',
∵ 照亮路面圆的面积为原来的2倍,
∴ 照亮路面圆的半径变为原来的2倍,
即OBOB'=OAOA'=12,
∴ 7.5OA'=12,
解得:OA'=7.5×2≈10.6(m),
则10.6-7.5=3.1(m),
答:原灯杆至少再增加3.1米.
【解答】
如图所示:
由题意可得:△AOB∽△A'OB',
∵ 照亮路面圆的面积为原来的2倍,
∴ 照亮路面圆的半径变为原来的2倍,
即OBOB'=OAOA'=12,
∴ 7.5OA'=12,
解得:OA'=7.5×2≈10.6(m),
则10.6-7.5=3.1(m),
答:原灯杆至少再增加3.1米.
25.
【答案】
证明:(1)∵ BF?//?DE,且AD=BD,
∴ AC=CG,
∴ BG=2CD,
∵ ∠C=90?,AD=BD,
∴ AB=2CD,
∴ AB=BG;
(2)∵ AC=3,BC=4,
∴ AB=5,
∴ CD=2.5,
∵ CE=13CD,
∴ DE=103,
∴ BF=2DE=203;
(3)由于AB=BG,∠C=90?,所以∠DBC=∠PBC.
第一种情况:若∠CDB=∠CPB,如图1:
在△BCP与△BCD中
∠CDB=∠CPB∠DBC=∠PBCBC=BC,
∴ △BCP?△BCD(AAS),
∴ BP=CD=2.5;
第二种情况:若∠PCB=∠CDB,过C点作CH⊥BG于H点.如图2:
∵ ∠CBD=∠CBP,
∴ △BPC∽△BCD,
∵ CH⊥BG,
∴ ∠ACB=∠CHB=90?,∠ABC=∠CBH,
∴ △ABC∽△CBH,
∴ ABCB=BCBH,
∴ BH=165,BP=325.
【解答】
证明:(1)∵ BF?//?DE,且AD=BD,
∴ AC=CG,
∴ BG=2CD,
∵ ∠C=90?,AD=BD,
∴ AB=2CD,
∴ AB=BG;
(2)∵ AC=3,BC=4,
∴ AB=5,
∴ CD=2.5,
∵ CE=13CD,
∴ DE=103,
∴ BF=2DE=203;
(3)由于AB=BG,∠C=90?,所以∠DBC=∠PBC.
第一种情况:若∠CDB=∠CPB,如图1:
在△BCP与△BCD中
∠CDB=∠CPB∠DBC=∠PBCBC=BC,
∴ △BCP?△BCD(AAS),
∴ BP=CD=2.5;
第二种情况:若∠PCB=∠CDB,过C点作CH⊥BG于H点.如图2:
∵ ∠CBD=∠CBP,
∴ △BPC∽△BCD,
∵ CH⊥BG,
∴ ∠ACB=∠CHB=90?,∠ABC=∠CBH,
∴ △ABC∽△CBH,
∴ ABCB=BCBH,
∴ BH=165,BP=325.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 若ab=52,则a+ba=( )
A.35 B.32 C.75 D.72
?
2. 如果mn=ab,那么下列比例式中错误的是(? ? ? ? )
A.am=nb B.an=mb C.ma=nb D.ma=bn
?
3. 点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于(? ? ? ? )
A.6cm B.(55+1)cm C.5(5-1)cm D.(55-1)cm
?
4. 如图,在△ABC中,∠BAC=90?,AD⊥BC,垂足为D,DE⊥AB,垂足为E,则图中与△ADE相似的三角形个数为(? ? ? ? )
A.1 B.2 C.3 D.4
?
5. 下列结论错误的是( )
A.等边三角形都相似 B.正方形都相似
C.所有长方形都相似 D.等腰直角三角形都相似
?
6. 如图,以点O为位似中心,将△ABC缩小后得到△A'B'C',已知OB=3OB',则△A'B'C'与△ABC的面积比为(? ? ? ? )
A.1:3 B.1:4 C.1:8 D.1:9
?
7. 如图,AD?//?EF?//?GH?//?PQ?//?BC,AE=EG=GP=PB,AD=2,BC=10,则EF、PQ长为( )
A.3和7 B.4和7 C.5和8 D.4和8
?
8. 如图,在△ABC中,点D、E分别在AB、AC上,AD=3,DB=2,DE?//?BC,则DE:BC的值是( )
A.32 B.23 C.94 D.35
?
9. 如图,以点O为位似中将△ABC放大后得到△DEF,已知△ABC与△DEF的面积比为1:9,则OC:CF的值为(? ? ? ? )
A.1:2 B.1:3 C.1:8 D.1:9
?
10. 如图,把△ABC绕点A旋转得到△ADE,当点D刚好落在BC上时,连结CE,设AC、DE相交于点F,则图中相似三角形的对数是(? ? ? ? ?)
A.3对 B.4对 C.5对 D.6对
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
11. 如图,△ABC的两条中线AD、BE相交于点G,如果AD=3,那么GD=________.
?12. 如图,根据图示,求得x和y的值分别为________.
?
13. 若a2=b3=c4,则3a+2b+ca=________.
?
14. 如果两个位似图形的对应线段长分别为2cm和6cm,且两个图形的面积之差为120cm2,则较大的图形的面积为________.
?
15. △ABC的各边之比为2:5:6,与其相似的另一个△A'B'C'的最大边为18cm,那么它的最小边为________.
?
16. 在四边形ABCD中,∠ABC=90?,对角线AC,BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=________.
?
17. 如图,D、E分别是△ABC的边AB、AC上的点,DE?//?BC,若ADDB=23,则AEEC=________.
?
18. 小亮希望测量出电线杆AB的高度,他在电线杆旁的点D处立一标杆,标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得DB=2ED米,CD=1.5米.则电线杆AB的高为________米.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 已知:线段a、b、c,且a2=b3=c4.
(1)求a+bb的值.
(2)如线段a、b、c满足a+b+c=27.求a、b、c的值.
?
20. 如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿 AB的长为3m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6m,请你计算旗杆DE的高度.
?
21. 如图,在△ABC中, DF//AC,DE//BC.
(1)求证: BFFC=CEEA;
(2)若AE=4,EC=2,BC=10,求BF和CF长.
?
22. 如图,在△AMC中,已知BD?//?CM,AC+AB=14,且AM:AD=4:3,求AB的长.
?
23. 如图,四边形OABC与四边形OA'B'C'是位似图形,AB与A'B'一定平行吗?为什么?
?
24. 某市在一道路拓宽改造过程中,发现原来道路两边的路灯除照亮路面的圆的面积不能满足需求外,亮度效果足以满图拓宽后的设计标准,因此,经设计人员研究,只要将路灯的灯标增加一定高度,使其照亮路面圆的面积为原来的2倍即可.已知原来路灯灯高为7.5米,请你求出原灯杆至少再增加多少米,才能符合拓宽后的设计要求?(精确到0.1米)
?
25. 如图,△ABC中,∠C=90?,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=13CD,过点B作BF?//?DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)求BF的长;
(3)若点P是射线BG上的一点,当BP的长为多少时,△BCP与△BCD相似?并说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
a+ba=1+ba
∵ ab=52
∴ ba=25
把ba=25代入a+ba=1+ba=75
2.
【答案】
C
【解答】
解:A、由am=nb得,ab=mn,故本选项不符合题意;
B、由an=mb得,ab=mn,故本选项不符合题意;
C、由ma=nb得,bm=an,故本选项符合题意;
D、由ma=bn得,ab=mn,故本选项不符合题意.
故选C.
3.
【答案】
C
【解答】
解:∵ 点C是线段AB的黄金分割点(AC>BC),
∴ AC=5-12AB,
而AB=10cm,
∴ AC=5-12×10=5(5-1)cm.
故选C.
4.
【答案】
D
【解答】
解:∵ AD⊥BC,DE⊥BA,
∴ ∠ADC=∠AED=90?,
∵ ∠BAC=90?,
∴ DE?//?AC,
∴ ∠ADE=∠DAC,
∴ △ADE?△CAD,
∴ ∠DAE=∠C,
∴ △ADE?△BAC,
∵ DE?//?AC,
∴ ∠BDE=∠C,
∴ △ADE?△BED.
∵ ∠AED=∠ADB=90?,
∴ △ADE?△ABD.
故选D.
5.
【答案】
C
【解答】
解:A、等边三角形都相似,正确,不合题意;
B、正方形都相似,正确,不合题意;
C、所有长方形不一定相似,故此选项错误,符合题意;
D、等腰直角三角形都相似,正确,不合题意;
故选:C.
6.
【答案】
D
【解答】
解:由位似变换的性质可知,A'B'?//?AB,A'C'?//?AC,
∴ OA'OA=OB'OB=13,
∴ A'C'AC=OA'OA=13,
∴ △A'B'C'与△ABC的相似比为1:3,
∴ △A'B'C'与△ABC的面积比为1:9,
故选D.
7.
【答案】
D
【解答】
解:过点D作DM?//?AB,交BC于点M,交EF、GH、PQ分别于点N、K、O,如下图所示:
∵ AD?//?BC,AB?//?DM,
∴ ABMD为平行四边形,
又AD?//?EF?//?GH?//?PQ?//?BC,
同理得到四边形AEND、AGKD、APOD都为平行四边形,
∴ AD=BM=EN=PO=2,
∴ CM=8,
∵ EF?//?BC,PQ?//?BC,AE=EG=GP=PB,
∴ NFMC=DFDC=14,OQCM=DQDC=34,
∴ NF=2,OQ=6,
∴ EF=EN+NF=4,PQ=PO+OQ=8.
故选D.
8.
【答案】
D
【解答】
解:∵ AD=3,DB=2,
∴ AB=AD+BD=3+2=5,
∵ DE?//?BC,
∴ DE:BC=AD:AB=3:5.
故选D.
9.
【答案】
A
【解答】
此题暂无解答
10.
【答案】
B
【解答】
解:∵ △ABC绕点A旋转得△ADE,
∴ △ABC?△ADE,∠AED=∠ACB,
∴ ∠EAF=∠FDC,
又∵ ∠AFE=∠DFC,
∴ △AFE?△DFC,
∴ AFDF=EFFC,
∵ ∠AFD=∠EFC,
∴ △AFD?△EFC,
∵ △ABC?△ADE,
∴ ∠BAC=∠DAE,AB=AD,AC=AE,
∴ ∠EAC=∠BAD,
∴ △AEC?△ABD.
∴ 共有4对相似三角形.
故选B.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
1
【解答】
解:∵ △ABC的两条中线AD、BE相交于点G,AD=3,
∴ 2GD=AG,
∴ GD=1,
故答案为:1.
12.
【答案】
4.5,101
【解答】
由图形可知:4.81.6=7.22.4=3,
∠ADC=∠BDE,
∴ △ADC∽△BDE,
∴ x1.5=3,
∴ x=4.5,
∠C=∠E=101?,
13.
【答案】
8
【解答】
解:根据题意,设a=2k,则b=3k,c=4k,
∴ 3a+2b+ca=6k+6k+4k2k=8.
14.
【答案】
135cm2
【解答】
解:∵ 两个位似图形的对应线段长分别为2cm和6cm,
∴ 其面积比为22:62=1:9,
∴ 设两正六边形的面积分别为x和9x,
根据题意列方程得,9x-x=120,
即8x=120,
解得:x=15.
则较大的图形的面积为:9×15=153(cm2).
故答案为:135cm2.
15.
【答案】
6cm
【解答】
解:∵ △ABC∽△A'B'C',△ABC的各边之比为2:5:6,
∴ △A'B'C'的各边之比为2:5:6,
∵ △A'B'C'的最大边为18cm,
∴ △A'B'C'的最小边为6cm.
16.
【答案】
154
【解答】
解:如图,过点A作AE⊥BD.
∵ CD⊥BD,AE⊥BD,
∴ ∠CDB=∠AED=90?,且AO=CO,∠COD=∠AOE,
∴ △AOE?△COD(AAS),
∴ CD=AE=3.
∵ ∠CDB=90?,CD=3,BC=5,
∴ DB?=?BC?2?-?CD?2?=?25?-?9?=?4.
∵ ∠ABC=∠AEB=90?,
∴ ∠ABE+∠EAB=90?,∠CBD+∠ABE=90?,
∴ ∠EAB=∠CBD,且∠CDB=∠AEB=90?,
∴ △ABE?△BCD,
∴ AEBD?=?ABBC,
∴ 34?=?AB5,
∴ AB?=?154.
故答案为:154.
17.
【答案】
23
【解答】
解:∵ DE?//?BC
∴ AEEC=ADDB=23.
18.
【答案】
4.5
【解答】
解:∵ CD?//?AB,
∴ △ECD∽△EAB,
∴ EDEB=CDAB,
∴ 13=1.5AB,
∴ AB=4.5(米).
故答案为;4.5.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:(1)∵ a2=b3,
∴ ab=23,
∴ a+bb=53,
(2)设a2=b3=c4=k,
则a=2k,b=3k,c=4k,
∵ a+b+c=27,
∴ 2k+3k+4k=27,
∴ k=3,
∴ a=6,b=9,c=12.
【解答】
解:(1)∵ a2=b3,
∴ ab=23,
∴ a+bb=53,
(2)设a2=b3=c4=k,
则a=2k,b=3k,c=4k,
∵ a+b+c=27,
∴ 2k+3k+4k=27,
∴ k=3,
∴ a=6,b=9,c=12.
20.
【答案】
解:(1)如图,线段EF就是旗杆DE在阳光下的投影.
作法:连接AC,过点D作DF//AC,交直线BE于点F,线段EF即为所求.
(2)∵ AC//DF,
∴ ∠ACB=∠DFE.
又∠ABC=∠DEF=90?,
∴ △ABC?△DEF,
∴ ABDE=BCEF.
∵ AB=3m,BC=2m,EF=6m,
∴ 3DE=26,
∴ DE=9m,
∴ 旗杆DE的高度为9m.
【解答】
解:(1)如图,线段EF就是旗杆DE在阳光下的投影.
作法:连接AC,过点D作DF//AC,交直线BE于点F,线段EF即为所求.
(2)∵ AC//DF,
∴ ∠ACB=∠DFE.
又∠ABC=∠DEF=90?,
∴ △ABC?△DEF,
∴ ABDE=BCEF.
∵ AB=3m,BC=2m,EF=6m,
∴ 3DE=26,
∴ DE=9m,
∴ 旗杆DE的高度为9m.
21.
【答案】
解:(1)∵ ?DF//AC,
∴ ?BFFC=BDDA.
∵ ?DE//BC,
∴ ?CEEA=BDDA,
∴ ?BFFC=CEEA.
(2)设BF=x,则CF=10-x.
由(1)得:BFFC=CEEA,
∴ ?x10-x=24,x=103,
∴ BF=103,CF=10-103=203.
【解答】
解:(1)∵ ?DF//AC,
∴ ?BFFC=BDDA.
∵ ?DE//BC,
∴ ?CEEA=BDDA,
∴ ?BFFC=CEEA.
(2)设BF=x,则CF=10-x.
由(1)得:BFFC=CEEA,
∴ ?x10-x=24,x=103,
∴ BF=103,CF=10-103=203.
22.
【答案】
解:∵ BD?//?CM,
∴ AC:AB=AM:AD=4:3,
∵ AC+AB=14,
∴ AC=47×14=8,AB=37×14=6,
∴ AB的长为6.
【解答】
解:∵ BD?//?CM,
∴ AC:AB=AM:AD=4:3,
∵ AC+AB=14,
∴ AC=47×14=8,AB=37×14=6,
∴ AB的长为6.
23.
【答案】
解:AB与A'B'一定平行,
∵ 四边形OABC与四边形OA'B'C'是位似图形,
∴ 四边形OABC∽四边形OA'B'C',
∴ ∠OAB=∠OA'B',
∴ AB?//?A'B'.
【解答】
解:AB与A'B'一定平行,
∵ 四边形OABC与四边形OA'B'C'是位似图形,
∴ 四边形OABC∽四边形OA'B'C',
∴ ∠OAB=∠OA'B',
∴ AB?//?A'B'.
24.
【答案】
由题意可得:△AOB∽△A'OB',
∵ 照亮路面圆的面积为原来的2倍,
∴ 照亮路面圆的半径变为原来的2倍,
即OBOB'=OAOA'=12,
∴ 7.5OA'=12,
解得:OA'=7.5×2≈10.6(m),
则10.6-7.5=3.1(m),
答:原灯杆至少再增加3.1米.
【解答】
如图所示:
由题意可得:△AOB∽△A'OB',
∵ 照亮路面圆的面积为原来的2倍,
∴ 照亮路面圆的半径变为原来的2倍,
即OBOB'=OAOA'=12,
∴ 7.5OA'=12,
解得:OA'=7.5×2≈10.6(m),
则10.6-7.5=3.1(m),
答:原灯杆至少再增加3.1米.
25.
【答案】
证明:(1)∵ BF?//?DE,且AD=BD,
∴ AC=CG,
∴ BG=2CD,
∵ ∠C=90?,AD=BD,
∴ AB=2CD,
∴ AB=BG;
(2)∵ AC=3,BC=4,
∴ AB=5,
∴ CD=2.5,
∵ CE=13CD,
∴ DE=103,
∴ BF=2DE=203;
(3)由于AB=BG,∠C=90?,所以∠DBC=∠PBC.
第一种情况:若∠CDB=∠CPB,如图1:
在△BCP与△BCD中
∠CDB=∠CPB∠DBC=∠PBCBC=BC,
∴ △BCP?△BCD(AAS),
∴ BP=CD=2.5;
第二种情况:若∠PCB=∠CDB,过C点作CH⊥BG于H点.如图2:
∵ ∠CBD=∠CBP,
∴ △BPC∽△BCD,
∵ CH⊥BG,
∴ ∠ACB=∠CHB=90?,∠ABC=∠CBH,
∴ △ABC∽△CBH,
∴ ABCB=BCBH,
∴ BH=165,BP=325.
【解答】
证明:(1)∵ BF?//?DE,且AD=BD,
∴ AC=CG,
∴ BG=2CD,
∵ ∠C=90?,AD=BD,
∴ AB=2CD,
∴ AB=BG;
(2)∵ AC=3,BC=4,
∴ AB=5,
∴ CD=2.5,
∵ CE=13CD,
∴ DE=103,
∴ BF=2DE=203;
(3)由于AB=BG,∠C=90?,所以∠DBC=∠PBC.
第一种情况:若∠CDB=∠CPB,如图1:
在△BCP与△BCD中
∠CDB=∠CPB∠DBC=∠PBCBC=BC,
∴ △BCP?△BCD(AAS),
∴ BP=CD=2.5;
第二种情况:若∠PCB=∠CDB,过C点作CH⊥BG于H点.如图2:
∵ ∠CBD=∠CBP,
∴ △BPC∽△BCD,
∵ CH⊥BG,
∴ ∠ACB=∠CHB=90?,∠ABC=∠CBH,
∴ △ABC∽△CBH,
∴ ABCB=BCBH,
∴ BH=165,BP=325.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
