京改版七年级上册3.10相交线与平行线(2) 课件(共37张PPT)
文档属性
| 名称 | 京改版七年级上册3.10相交线与平行线(2) 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:17:18 | ||
图片预览







文档简介
相交线与平行线(2)
初一年级 数学
【实践一】
如图,点P是直线 l 外一点,过点P作直线 l 的垂线,垂足为点A.
一、引 入
一、引 入
【实践一】
如图,点P是直线 l 外一点,过点P作直线 l 的垂线,垂足为点A.
1.定义:从直线外一点向这条直线引垂线,该点到
垂足之间的线段叫做垂线段.
(一)点到直线的距离
二、新 知
线段PA是点P到直线 l 的
垂线段
2.定义:从直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离.
(一)点到直线的距离
PA=3.6cm
点P到直线 l 的距离是3.6cm
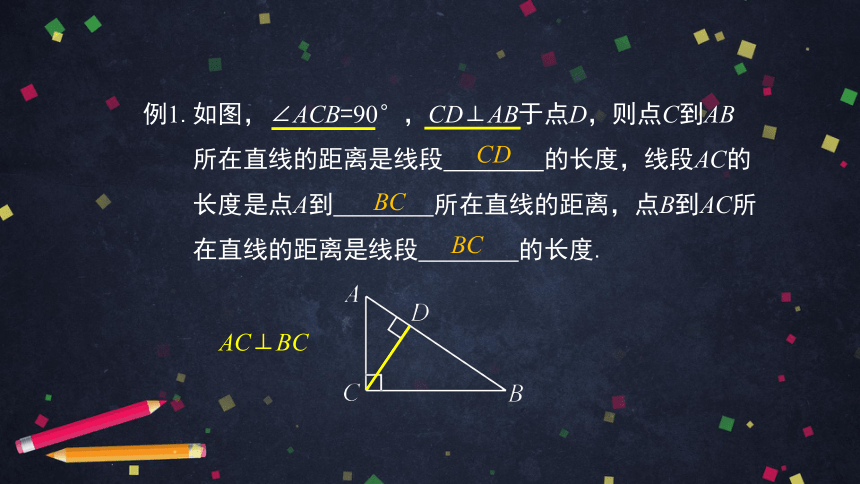
例1.如图,∠ACB=90°,CD⊥AB于点D,则点C到AB
所在直线的距离是线段 的长度,线段AC的
长度是点A到 所在直线的距离,点B到AC所
在直线的距离是线段 的长度.
CD
BC
BC
AC⊥BC
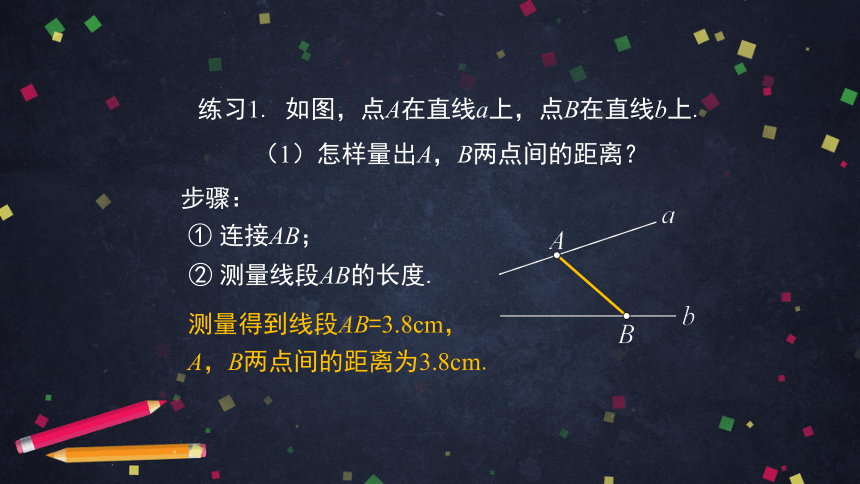
练习1. 如图,点A在直线a上,点B在直线b上.
(1)怎样量出A,B两点间的距离?
(2)怎样量出点A到直线b的距离?
(3)怎样量出点B到直线a的距离?
练习1. 如图,点A在直线a上,点B在直线b上.
(1)怎样量出A,B两点间的距离?
步骤:
① 连接AB;
② 测量线段AB的长度.
测量得到线段AB=3.8cm,
A,B两点间的距离为3.8cm.
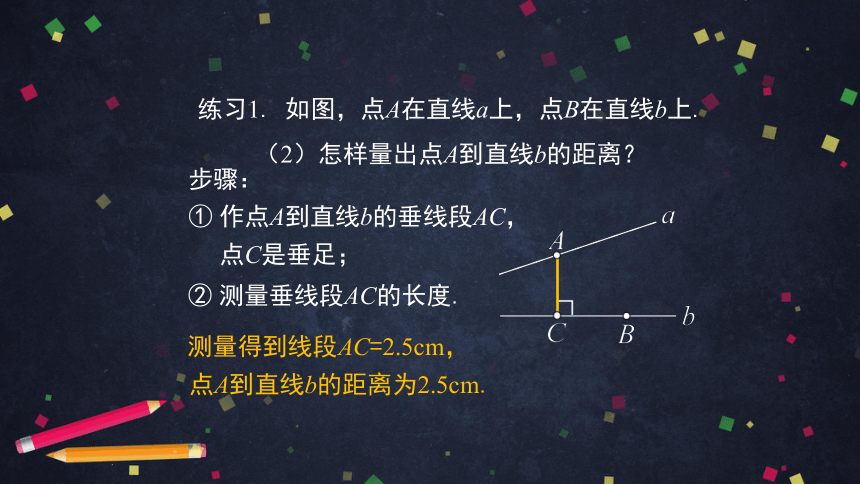
② 测量垂线段AC的长度.
步骤:
① 作点A到直线b的垂线段AC,
点C是垂足;
测量得到线段AC=2.5cm,
点A到直线b的距离为2.5cm.
练习1. 如图,点A在直线a上,点B在直线b上.
(2)怎样量出点A到直线b的距离?
② 测量垂线段BD的长度.
步骤:
① 作点B到直线a的垂线段BD,
点D是垂足;
测量得到线段BD=3.4cm,
点B到直线a的距离为3.4cm.
练习1. 如图,点A在直线a上,点B在直线b上.
(3)怎样量出点B到直线a的距离?
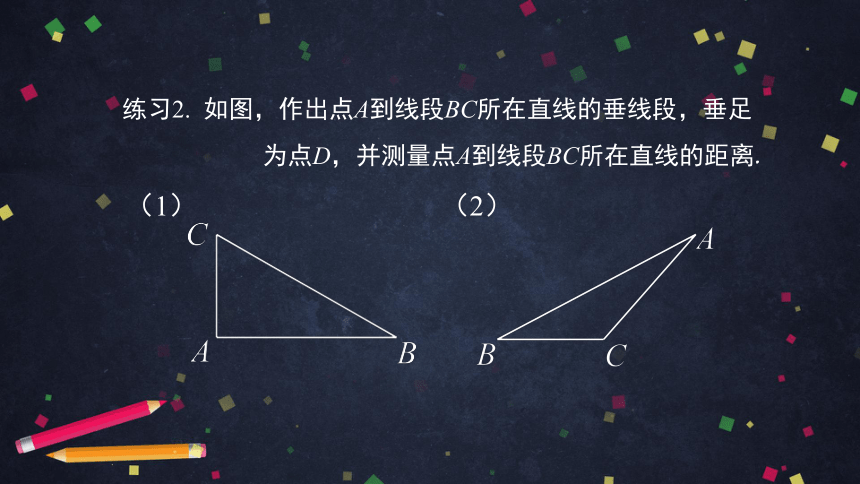
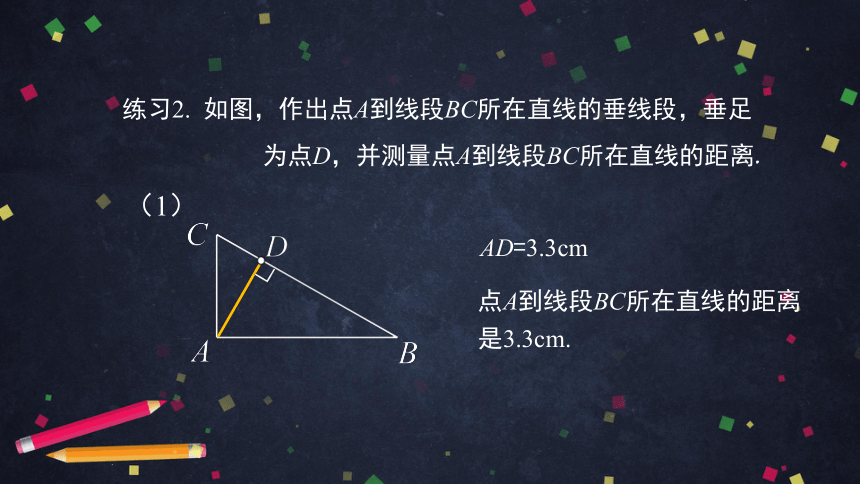
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
(1)
(2)
AD=3.3cm
点A到线段BC所在直线的距离
是3.3cm.
(1)
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
(2)
AD=4cm
点A到线段BC所在直线的距离
是4cm.
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
【思考】
跳远比赛时,如何测量运动员的跳远成绩呢?
【思考】
跳远比赛时,如何测量运动员的跳远成绩呢?
把靠后的那只脚的后脚跟抽象为一个点,
测量这个点到起跳线的距离.
【实践二】
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
① 连接PB,PC ,PD;
② 测量线段PA,PB,PC,PD的长度,
从中能发现什么结论?
【实践二】
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
① 连接PB,PC ,PD;
② 测量线段PA,PB,PC,PD的长度,
从中能发现什么结论?
【实践二】
PA=4.5cm
PC=5cm
PD=5.7cm
PB=6.4cm
垂线段PA是最短的.
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
3.结论:直线外一点与直线上各点连接的所有线段中,
垂线段最短. 简称,垂线段最短.
例2.如图,计划把河中的水引到水池C中,可以先作CD⊥AB,
垂足为D,然后沿CD开渠,则能使水渠最短,这种设计
方案的根据是 .
垂线段最短
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
PQ=2cm
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
①当PQ⊥l 时:
点P到直线 l 的距离是2cm.
②当PQ与 l 不垂直时:
点P到直线 l 的距离小于2cm.
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
C
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
如图,让直线PA绕点P旋转起来,使之与直线 l 没有交点,此时直线PA与直线 l 是什么位置关系呢?
如图,让直线PA绕点P旋转起来,使之与直线 l 没有交点,此时直线PA与直线 l 是什么位置关系呢?
直线PA与直线 l
互相平行
日常生活中我们见到笔直的列车轨道和斑马线,都给
我们平行的印象:
1.定义:在同一平面内,不相交的两条直线叫做平行线.
也说这两条直线互相平行.
(二)平行线
(二)平行线
2.表示方法:
平行用符号“∥”表示,读作“平行于”.
直线a与b互相平行,记作a∥b或b∥a.
注意:
定义中,不能直接说“不相交的两条直线叫做平行线”,
必须加上“在同一平面内”. 如图,在长方体中,直线
GF和直线AB没有公共点、不相交,但却不是平行线,
因为它们不在同一平面内.
练习:观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
AB DC,AD AB,DH HG,AE BF;
∥
⊥
⊥
∥
练习:观察图中所示的长方体,完成填空:
(2)DC和BF所在直线是两条不相交的直线,它们
(填“是”或“不是”)平行线,因为
只有 内,两条不相交的直线才
能叫做平行线.
不是
在同一平面
相交
一个角
等于90°
两条直线
互相垂直
概念及表示方法
垂线的画法
垂线段的概念
点到直线的距离
不相交
在同一平面内:互相平行
不在同一平面内
三、总 结
两条直线的
位置关系
四、作 业
1.作出点B到线段AC所在直线的垂线段,垂足为点D,
并测量点B到线段AC所在直线的距离.
(2)
(1)
2.观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
HD GC,FB AB;
(2)AD和GC所在直线 (填“是”或“不
是”)平行线,理由是 .
同学们,再见!
初一年级 数学
【实践一】
如图,点P是直线 l 外一点,过点P作直线 l 的垂线,垂足为点A.
一、引 入
一、引 入
【实践一】
如图,点P是直线 l 外一点,过点P作直线 l 的垂线,垂足为点A.
1.定义:从直线外一点向这条直线引垂线,该点到
垂足之间的线段叫做垂线段.
(一)点到直线的距离
二、新 知
线段PA是点P到直线 l 的
垂线段
2.定义:从直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离.
(一)点到直线的距离
PA=3.6cm
点P到直线 l 的距离是3.6cm
例1.如图,∠ACB=90°,CD⊥AB于点D,则点C到AB
所在直线的距离是线段 的长度,线段AC的
长度是点A到 所在直线的距离,点B到AC所
在直线的距离是线段 的长度.
CD
BC
BC
AC⊥BC
练习1. 如图,点A在直线a上,点B在直线b上.
(1)怎样量出A,B两点间的距离?
(2)怎样量出点A到直线b的距离?
(3)怎样量出点B到直线a的距离?
练习1. 如图,点A在直线a上,点B在直线b上.
(1)怎样量出A,B两点间的距离?
步骤:
① 连接AB;
② 测量线段AB的长度.
测量得到线段AB=3.8cm,
A,B两点间的距离为3.8cm.
② 测量垂线段AC的长度.
步骤:
① 作点A到直线b的垂线段AC,
点C是垂足;
测量得到线段AC=2.5cm,
点A到直线b的距离为2.5cm.
练习1. 如图,点A在直线a上,点B在直线b上.
(2)怎样量出点A到直线b的距离?
② 测量垂线段BD的长度.
步骤:
① 作点B到直线a的垂线段BD,
点D是垂足;
测量得到线段BD=3.4cm,
点B到直线a的距离为3.4cm.
练习1. 如图,点A在直线a上,点B在直线b上.
(3)怎样量出点B到直线a的距离?
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
(1)
(2)
AD=3.3cm
点A到线段BC所在直线的距离
是3.3cm.
(1)
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
(2)
AD=4cm
点A到线段BC所在直线的距离
是4cm.
练习2. 如图,作出点A到线段BC所在直线的垂线段,垂足
为点D,并测量点A到线段BC所在直线的距离.
【思考】
跳远比赛时,如何测量运动员的跳远成绩呢?
【思考】
跳远比赛时,如何测量运动员的跳远成绩呢?
把靠后的那只脚的后脚跟抽象为一个点,
测量这个点到起跳线的距离.
【实践二】
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
① 连接PB,PC ,PD;
② 测量线段PA,PB,PC,PD的长度,
从中能发现什么结论?
【实践二】
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
① 连接PB,PC ,PD;
② 测量线段PA,PB,PC,PD的长度,
从中能发现什么结论?
【实践二】
PA=4.5cm
PC=5cm
PD=5.7cm
PB=6.4cm
垂线段PA是最短的.
如图,已知PA与直线 l 垂直,垂足为点A,点B,C,D是直线
l 上不与点A重合的任意三点.
3.结论:直线外一点与直线上各点连接的所有线段中,
垂线段最短. 简称,垂线段最短.
例2.如图,计划把河中的水引到水池C中,可以先作CD⊥AB,
垂足为D,然后沿CD开渠,则能使水渠最短,这种设计
方案的根据是 .
垂线段最短
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
PQ=2cm
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
①当PQ⊥l 时:
点P到直线 l 的距离是2cm.
②当PQ与 l 不垂直时:
点P到直线 l 的距离小于2cm.
例3.直线 l 外一点P到直线 l 上一点Q的距离是2cm,则点P到
直线 l 的距离( )
C
A.等于2cm B.小于2cm
C.小于或等于2cm D.大于2cm
如图,让直线PA绕点P旋转起来,使之与直线 l 没有交点,此时直线PA与直线 l 是什么位置关系呢?
如图,让直线PA绕点P旋转起来,使之与直线 l 没有交点,此时直线PA与直线 l 是什么位置关系呢?
直线PA与直线 l
互相平行
日常生活中我们见到笔直的列车轨道和斑马线,都给
我们平行的印象:
1.定义:在同一平面内,不相交的两条直线叫做平行线.
也说这两条直线互相平行.
(二)平行线
(二)平行线
2.表示方法:
平行用符号“∥”表示,读作“平行于”.
直线a与b互相平行,记作a∥b或b∥a.
注意:
定义中,不能直接说“不相交的两条直线叫做平行线”,
必须加上“在同一平面内”. 如图,在长方体中,直线
GF和直线AB没有公共点、不相交,但却不是平行线,
因为它们不在同一平面内.
练习:观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
AB DC,AD AB,DH HG,AE BF;
∥
⊥
⊥
∥
练习:观察图中所示的长方体,完成填空:
(2)DC和BF所在直线是两条不相交的直线,它们
(填“是”或“不是”)平行线,因为
只有 内,两条不相交的直线才
能叫做平行线.
不是
在同一平面
相交
一个角
等于90°
两条直线
互相垂直
概念及表示方法
垂线的画法
垂线段的概念
点到直线的距离
不相交
在同一平面内:互相平行
不在同一平面内
三、总 结
两条直线的
位置关系
四、作 业
1.作出点B到线段AC所在直线的垂线段,垂足为点D,
并测量点B到线段AC所在直线的距离.
(2)
(1)
2.观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
HD GC,FB AB;
(2)AD和GC所在直线 (填“是”或“不
是”)平行线,理由是 .
同学们,再见!
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
