人教版八年级数学上册15.2 分式的运算课件(34张ppt)
文档属性
| 名称 | 人教版八年级数学上册15.2 分式的运算课件(34张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 05:34:40 | ||
图片预览







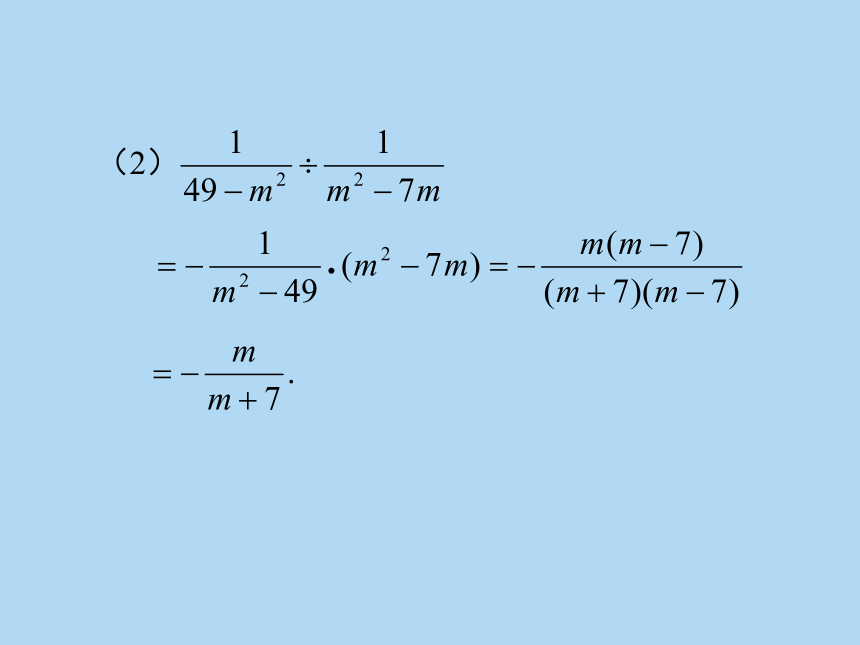




文档简介
15.2 分式的运算
教学目标
1.类比分数的四则运算法则,探究分式的四则运算,掌握这些法则.
2. 能熟练借助分式的运算法则进行相关计算.
3.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相互联系的知识体系.
教学重点与难点
分式的四则运算.
分式的乘除
问题 1 一个水平放置的长方体容器,其容积为V,
底面的长为a,宽为b,当容器内的水占容积的 时,
水面的高度为多少?
长方体容器的高为 ,水面的高度为 .
问题 2 大拖拉机 m天耕地a hm2,小拖拉机n 天耕地b hm2,大拖拉机的工作效率是小拖拉机的工作效率的多少倍?
大拖拉机的工作效率是 hm2/天,小拖拉机的工作效率是 hm2/天,大拖拉机的工作效率是小拖拉机工作效率的 倍.
从上面的问题可知,为讨论数量关系有时需要进行分式的乘除运算.
分式与分数具有类似的形式,我们可以类比分数的运算法则认识分式的运算法则.
思考
你还记得分数的乘除法法则吗?类比分数的乘除法法则,你能说出分式的乘除法法则吗?
类似于分数,分式有:
乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则可以用式子表示为
例 1 计算:
(1) ;
(2) .
解:(1) ;
(2)
例 2 计算:
(1) ;
(2) .
解:(1)
(2)
例 3 如下图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m 的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)m 的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
解:(1)“丰收1号”小麦的试验田面积是(a2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是 (a-1)2 m2 ,单位面积产量是
kg/m2 .
∵ a>1,
∴ (a-1)2>0,a2-1>0.
由上右图可得(a-1)2<a2-1 .
∴ <
所以,“丰收2号”小麦的单位面积产量高.
(2)
所以,“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
例 4 计算:
解:
思考
根据乘方的意义和分式的乘法法则,可得:
;
.
一般地,当n 是正整数时,
n 个
n 个
n 个
这就是说,分式乘方要把分子、分母分别乘方.
例 5 计算:
(1)
(2)
解:(1)
(2)
分式的加减
问题3 甲工程队完成一项工程需n天,乙工程队要比甲队多用 3 天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
甲工程队一天完成这项工程的 ,乙工程队一天完成这项工程的 ,两队共同工作一天完成这项工程的( + ).
问题4 2009年、2010年、2011年某地的森林面积(单位:km2)分别是 S1,S2,S3,2011年与2010年相比,森林面积增长率提高了多少?
2011年的森林面积增长率是 ,2010 年的森林面积增长率是 ,2011年与2010年相比,森林面积增长率提高了 - .
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算.
思考
分式的加减法与分数的加减法类似,它们的实质相同.观察下列分数加减运算的式子:
.你能将它们推广,得出分式的加减法法则吗?
类似分数的加减法,分式的加减法法则是:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
例 6 计算:
(1)
(2)
解:(1)
(2)
例 7 计算:
解:
例 8 计算:
(1)
(2)
解:(1)
(2)
整数指数幂
我们知道,当n 是正整数时,
an=a·a·…·a.
n 个
正整数指数幂有以下运算性质:
(1)a m·a n=a m+n(m,n 是正整数);
(2)(a m)n=a mn(m,n 是正整数);
(3)(ab)n=anbn(n 是正整数);
(4)a m÷a n=a m-n(a≠0,m,n是正整数,
m>n);
其中,第(5)个性质就是分式的乘方法则.
此外,我们还学习过 0 指数幂,即当a≠ 0时,a 0=1.
(5) (n是正整数).
思考
a m中指数m可以是负整数吗?如果可以,那么负整数指数幂a m表示什么?
由分式的约分可知,当a≠0时,
①
另一方面,如果把正整数指数幂的运算性质(4)
a m÷a n=a m-n(a≠0,m,n是正整数,m>n)中的条件m>n去掉,即假设这个性质对于像a 3÷a 5的情形也能使用,则有
a 3÷a 5 =a 3-5=a -2.
②
由①②两式,我们想到如果规定 (a≠0),
就能使a m÷a n=a m-n 这条性质也适用于像 a 3÷a 5 这样的情形.为使上述运算性质适用范围更广,同时也可以更简便地表示分式,数学中规定:
一般地,当 n 是正整数时
(a≠ 0).
这就是说,a-n(a≠0)是a n 的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数.
思考
引入负整数指数和0指数后, a m·an=a m+n (m,n是正整数)这条性质能否推广到m,n 是任意整数的情形?
我们从特殊情形入手进行研究.例如,
归纳
a m·a n=a m+n 这条性质对于m,n 是任意整数的情形仍然适用.
探究
类似地,你可以用负整数指数幂或 0 指数幂对于其他正整数指数幂的运算性质进行试验,看看这些性质在整数指数幂范围内是否还适用.
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
例 9 计算:
(1)a-2÷a5;
(2)
(1)(a-1b2)3;
(4)a-2b2·(a2b-2)-3.
解:(1) a-2÷a5=a-2-5=a-7
(2)
(3) (a-1b2)3=a-3b6
(4)a-2b2·(a2b-2)-3=a-2b2·a-6b6=a-8b8
(1)am·an =am+n(m,n是整数);
(2)(am)n =amn(m,n是整数);
(3)(ab)n =anbn(m,n是整数).
根据整数指数幂的运算性质,当m,n为整数时, am÷an=am-n,am·a-n=am+(-n )=am-n,因此am÷an=am·a-n,即同底数幂的除法am÷an可以转化为同底
数幂的乘法am·a-n.特别地, =a÷b=a·b-1,所以, =(a·b-1)n ,即商的乘方 可以转化为积的乘方(a·b-1)n.这样,整数指数幂的运算性质可以归结为:
例10 纳米(nm)是非常小的长度单位,1 nm=10-9m.把1 nm3的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
解:1 mm=10-3m,1 nm=10-9m.
(10-3)3÷(10-9)3=10-9÷10-27=10-9-(-27)
=1018.
1 mm3的空间可以放1018个1 nm3的物体.
1018是一个非常大的数,它是 1 亿(即108)的100 亿(即1010)倍.
再见!
教学目标
1.类比分数的四则运算法则,探究分式的四则运算,掌握这些法则.
2. 能熟练借助分式的运算法则进行相关计算.
3.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相互联系的知识体系.
教学重点与难点
分式的四则运算.
分式的乘除
问题 1 一个水平放置的长方体容器,其容积为V,
底面的长为a,宽为b,当容器内的水占容积的 时,
水面的高度为多少?
长方体容器的高为 ,水面的高度为 .
问题 2 大拖拉机 m天耕地a hm2,小拖拉机n 天耕地b hm2,大拖拉机的工作效率是小拖拉机的工作效率的多少倍?
大拖拉机的工作效率是 hm2/天,小拖拉机的工作效率是 hm2/天,大拖拉机的工作效率是小拖拉机工作效率的 倍.
从上面的问题可知,为讨论数量关系有时需要进行分式的乘除运算.
分式与分数具有类似的形式,我们可以类比分数的运算法则认识分式的运算法则.
思考
你还记得分数的乘除法法则吗?类比分数的乘除法法则,你能说出分式的乘除法法则吗?
类似于分数,分式有:
乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则可以用式子表示为
例 1 计算:
(1) ;
(2) .
解:(1) ;
(2)
例 2 计算:
(1) ;
(2) .
解:(1)
(2)
例 3 如下图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m 的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)m 的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
解:(1)“丰收1号”小麦的试验田面积是(a2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是 (a-1)2 m2 ,单位面积产量是
kg/m2 .
∵ a>1,
∴ (a-1)2>0,a2-1>0.
由上右图可得(a-1)2<a2-1 .
∴ <
所以,“丰收2号”小麦的单位面积产量高.
(2)
所以,“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
例 4 计算:
解:
思考
根据乘方的意义和分式的乘法法则,可得:
;
.
一般地,当n 是正整数时,
n 个
n 个
n 个
这就是说,分式乘方要把分子、分母分别乘方.
例 5 计算:
(1)
(2)
解:(1)
(2)
分式的加减
问题3 甲工程队完成一项工程需n天,乙工程队要比甲队多用 3 天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
甲工程队一天完成这项工程的 ,乙工程队一天完成这项工程的 ,两队共同工作一天完成这项工程的( + ).
问题4 2009年、2010年、2011年某地的森林面积(单位:km2)分别是 S1,S2,S3,2011年与2010年相比,森林面积增长率提高了多少?
2011年的森林面积增长率是 ,2010 年的森林面积增长率是 ,2011年与2010年相比,森林面积增长率提高了 - .
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算.
思考
分式的加减法与分数的加减法类似,它们的实质相同.观察下列分数加减运算的式子:
.你能将它们推广,得出分式的加减法法则吗?
类似分数的加减法,分式的加减法法则是:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
例 6 计算:
(1)
(2)
解:(1)
(2)
例 7 计算:
解:
例 8 计算:
(1)
(2)
解:(1)
(2)
整数指数幂
我们知道,当n 是正整数时,
an=a·a·…·a.
n 个
正整数指数幂有以下运算性质:
(1)a m·a n=a m+n(m,n 是正整数);
(2)(a m)n=a mn(m,n 是正整数);
(3)(ab)n=anbn(n 是正整数);
(4)a m÷a n=a m-n(a≠0,m,n是正整数,
m>n);
其中,第(5)个性质就是分式的乘方法则.
此外,我们还学习过 0 指数幂,即当a≠ 0时,a 0=1.
(5) (n是正整数).
思考
a m中指数m可以是负整数吗?如果可以,那么负整数指数幂a m表示什么?
由分式的约分可知,当a≠0时,
①
另一方面,如果把正整数指数幂的运算性质(4)
a m÷a n=a m-n(a≠0,m,n是正整数,m>n)中的条件m>n去掉,即假设这个性质对于像a 3÷a 5的情形也能使用,则有
a 3÷a 5 =a 3-5=a -2.
②
由①②两式,我们想到如果规定 (a≠0),
就能使a m÷a n=a m-n 这条性质也适用于像 a 3÷a 5 这样的情形.为使上述运算性质适用范围更广,同时也可以更简便地表示分式,数学中规定:
一般地,当 n 是正整数时
(a≠ 0).
这就是说,a-n(a≠0)是a n 的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数.
思考
引入负整数指数和0指数后, a m·an=a m+n (m,n是正整数)这条性质能否推广到m,n 是任意整数的情形?
我们从特殊情形入手进行研究.例如,
归纳
a m·a n=a m+n 这条性质对于m,n 是任意整数的情形仍然适用.
探究
类似地,你可以用负整数指数幂或 0 指数幂对于其他正整数指数幂的运算性质进行试验,看看这些性质在整数指数幂范围内是否还适用.
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
例 9 计算:
(1)a-2÷a5;
(2)
(1)(a-1b2)3;
(4)a-2b2·(a2b-2)-3.
解:(1) a-2÷a5=a-2-5=a-7
(2)
(3) (a-1b2)3=a-3b6
(4)a-2b2·(a2b-2)-3=a-2b2·a-6b6=a-8b8
(1)am·an =am+n(m,n是整数);
(2)(am)n =amn(m,n是整数);
(3)(ab)n =anbn(m,n是整数).
根据整数指数幂的运算性质,当m,n为整数时, am÷an=am-n,am·a-n=am+(-n )=am-n,因此am÷an=am·a-n,即同底数幂的除法am÷an可以转化为同底
数幂的乘法am·a-n.特别地, =a÷b=a·b-1,所以, =(a·b-1)n ,即商的乘方 可以转化为积的乘方(a·b-1)n.这样,整数指数幂的运算性质可以归结为:
例10 纳米(nm)是非常小的长度单位,1 nm=10-9m.把1 nm3的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
解:1 mm=10-3m,1 nm=10-9m.
(10-3)3÷(10-9)3=10-9÷10-27=10-9-(-27)
=1018.
1 mm3的空间可以放1018个1 nm3的物体.
1018是一个非常大的数,它是 1 亿(即108)的100 亿(即1010)倍.
再见!
